Chapter 3, Problem 1RP

Program Plan Intro

Linear programming (LP):

• The linear programming(LP) is also known as linear optimization.
• Consider a mathematical model, and its requirements are used to represent by the linear relationships. The linear programming is the best method to achieve the best outcome of this mathematical model. The outcomes may be, maximum profit or lower cost.
• The linear optimization is also called as mathematical optimization because, it is a special case of mathematical programming.
• More formally, the LP is a technique for optimizing linear objective function subject to constraints of linear equality and linear inequality.

Explanation of Solution

Linear programming for solving the problem:

  Let $\text{x}$= barrels of beer produced

  $\text{y}$= barrels of ale produced

  Then,

  $\begin{array}{l}\max z=5x+2y\\ 5x+2y\le 60\\ 2x+y\le 25\\ x,y\ge 0\end{array}$

Explanation:

• The above programming statements are used to solve the beer and ale problem. In this there are two variables “x” and “y” used to represent the barrels of beer produced and barrels of ale produced respectively.
• The above statements give the formula to maximize the profit. Which is “5x + 2y”.

Solving LP graphically:

	Beer	Ale	Total
Corn	5lb	2lb	60
Hopes	2lb	1lb	25

Let $\text{x}$=amount of beer

$\text{y}$=amount of ale

$\begin{array}{l}\text{5x+2y}\le \text{60,x}\ge \text{0}\\ \text{2x+1y}\le \text{25,y}\ge \text{0}\\ \text{maximize=5x+2y}\end{array}$

LP graph:

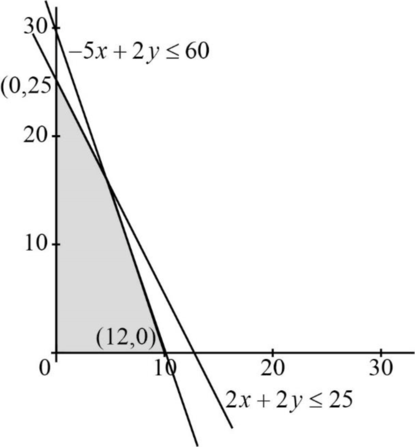
Vertices are, $(12,0),(10,5),(0,25)$

Profit function: $5x+2y$

The profit function at $(12,0)$$=5\times 12+2\times 0=60$

The profit function at $(0,25)$$=5\times 0+2\times 25=50$

The profit function at $(10,5)$$=5\times 10+5\times 2=50+10=60$

The profit is maximized at the points, $(10,5)$ and $(12,0)$.

That is 10 barrels of beer and 5 barrels of ale.