
Weighted Graph:
A graph is termed as weighted graph if each edge of the graph is assigned a weight. The weighted edges stored in the weighted graphs can be stored in adjacency lists.
Weighted edges can be represented using a two-dimensional array. An weighted edge can be represented as “WeightedEdge(u,v,w)”, where “u” and “v” are edges and “w” represents the weight between them.
Example of storing edge in a weighted graph:
Object[][] edges =
{ new Integer(0), new Integer(1), new SomeTypeForWeight(8) };
Prim’s
Prim’s Algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph by finding a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
Time Complexity of Prim’s algorithm:
Prim’s Algorithm Steps using adjacency matrix to store the weighted edges:
Step 1: Select a random vertex v, add v to S, assign an array A where A[i] = d{v, i}
Step 2: While there are vertices that belong to G and not to S do:
2.1. Iterate through A, select the minimum value A[i], add vertex i to S
2.2. for each edge e={i, j} connected to vertex i do:
2.2.1. if d{i, j} < A[j] then A[j] = d{i ,j}
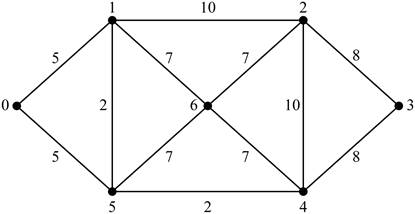
Given Graph:
Want to see the full answer?
Check out a sample textbook solution
Chapter 29 Solutions
MyLab Programming with Pearson eText -- Access Card -- for Introduction to Java Programming and Data Structures, Comprehensive Version
- Given f(t)=a sin(ßt) a = 10 & ß = 23 Find the Laplace Transform using the definition F(s) = ∫f(t)e-stdtarrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardObtain the MUX design for the function F(X,Y,Z) = (0,3,4,7) using an off-the-shelf MUX with an active low strobe input (E).arrow_forward
- I cannot program smart home automation rules from my device using a computer or phone, and I would like to know how to properly connect devices such as switches and sensors together ? Cisco Packet Tracer 1. Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardusing r language for integration theta = integral 0 to infinity (x^4)*e^(-x^2)/2 dx (1) use the density function of standard normal distribution N(0,1) f(x) = 1/sqrt(2pi) * e^(-x^2)/2 -infinity <x<infinity as importance function and obtain an estimate theta 1 for theta set m=100 for the estimate whatt is the estimate theta 1? (2)use the density function of gamma (r=5 λ=1/2)distribution f(x)=λ^r/Γ(r) x^(r-1)e^(-λx) x>=0 as importance function and obtain an estimate theta 2 for theta set m=1000 fir the estimate what is the estimate theta2? (3) use simulation (repeat 1000 times) to estimate the variance of the estimates theta1 and theta 2 which one has smaller variance?arrow_forwardusing r language A continuous random variable X has density function f(x)=1/56(3x^2+4x^3+5x^4).0<=x<=2 (1) secify the density g of the random variable Y you find for the acceptance rejection method. (2) what is the value of c you choose to use for the acceptance rejection method (3) use the acceptance rejection method to generate a random sample of size 1000 from the distribution of X .graph the density histogram of the sample and compare it with the density function f(x)arrow_forward
- using r language a continuous random variable X has density function f(x)=1/4x^3e^-(pi/2)^4,x>=0 derive the probability inverse transformation F^(-1)x where F(x) is the cdf of the random variable Xarrow_forwardusing r language in an accelerated failure test, components are operated under extreme conditions so that a substantial number will fail in a rather short time. in such a test involving two types of microships 600 chips manufactured by an existing process were tested and 125 of them failed then 800 chips manufactured by a new process were tested and 130 of them failed what is the 90%confidence interval for the difference between the proportions of failure for chips manufactured by two processes? using r languagearrow_forwardI want a picture of the tools and the pictures used Cisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forward
- A. What will be printed executing the code above?B. What is the simplest way to set a variable of the class Full_Date to January 26 2020?C. Are there any empty constructors in this class Full_Date?a. If there is(are) in which code line(s)?b. If there is not, how would an empty constructor be? (create the code lines for it)D. Can the command std::cout << d1.m << std::endl; be included after line 28 withoutcausing an error?a. If it can, what will be printed?b. If it cannot, how could this command be fixed?arrow_forwardCisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardTransform the TM below that accepts words over the alphabet Σ= {a, b} with an even number of a's and b's in order that the output tape head is positioned over the first letter of the input, if the word is accepted, and all letters a should be replaced by the letter x. For example, for the input aabbaa the tape and head at the end should be: [x]xbbxx z/z,R b/b,R F ① a/a,R b/b,R a/a, R a/a,R b/b.R K a/a,R L b/b,Rarrow_forward
 Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning
New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning





