
Concept explainers
(a)
The magnitude and direction of magnetic field at point A
(a)
Answer to Problem 7P
Explanation of Solution
Given Info: The current flowing through the conductor is
Explanation:
Diagram of three parallel conductor having current of magnitude
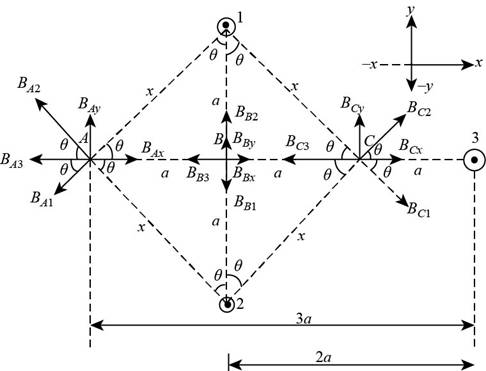
Figure (1)
Formula to calculate side of the square is,
Formula to calculate angle
Formula to calculate magnetic field at point
Here
Substitute
Formula to calculate magnetic field at point
Here
Substitute
Formula to calculate magnetic field at point
Here
Substitute
Write the expression to calculate magnetic field at point
Here,
Substitute
substitute
Write the expression to calculate y-component of magnetic field at
Substitute
Formula to calculate net magnetic field at point
Substitute
Hence, magnetic field at point
Conclusion:
Therefore magnetic field at point
(b)
magnitude and direction of magnetic field at point B
(b)
Answer to Problem 7P
Explanation of Solution
Formula to calculate magnetic field at point
Here
Substitute
Formula to calculate magnetic field at point
Here
Substitute
Formula to calculate magnetic field at point
Here
Substitute
Write the expression to calculate magnetic field at point
Here,
Substitute
substitute
Write the expression to calculate y-component of magnetic field at
Substitute
Formula to calculate net magnetic field at point
Substitute
Hence, magnetic field at point
Conclusion:
Therefore magnetic field at point
(c)
magnitude and direction of magnetic field at point C
(c)
Answer to Problem 7P
Explanation of Solution
Formula to calculate magnetic field at point
Here
Substitute
Formula to calculate magnetic field at point
Here
Substitute
Formula to calculate magnetic field at point
Here
Substitute
Write the expression to calculate magnetic field at point
Here,
Substitute
Write the expression to calculate y-component of magnetic field at
Substitute
Formula to calculate net magnetic field at point
Substitute
Hence, magnetic field at point
Conclusion:
Therefore magnetic field at point
Want to see more full solutions like this?
Chapter 29 Solutions
PHYSICS:F/SCI.+ENGRS-W/WEBASSIGN
- Sketch a sine wave depicting 3 seconds of wave activity for a 5 Hz tone.arrow_forwardThe drawing shows two long, straight wires that are suspended from the ceiling. The mass per unit length of each wire is 0.050 kg/m. Each of the four strings suspending the wires has a length of 1.2 m. When the wires carry identical currents in opposite directions, the angle between the strings holding the two wires is 20°. (a) Draw the free-body diagram showing the forces that act on the right wire with respect to the x axis. Account for each of the strings separately. (b) What is the current in each wire? 1.2 m 20° I -20° 1.2 marrow_forwardplease solve thisarrow_forward
- please solve everything in detailarrow_forward6). What is the magnitude of the potential difference across the 20-02 resistor? 10 Ω 11 V - -Imm 20 Ω 10 Ω 5.00 10 Ω a. 3.2 V b. 7.8 V C. 11 V d. 5.0 V e. 8.6 Varrow_forward2). How much energy is stored in the 50-μF capacitor when Va - V₁ = 22V? 25 µF b 25 µF 50 µFarrow_forward
- 9). A series RC circuit has a time constant of 1.0 s. The battery has a voltage of 50 V and the maximum current just after closing the switch is 500 mA. The capacitor is initially uncharged. What is the charge on the capacitor 2.0 s after the switch is closed? R 50 V a. 0.43 C b. 0 66 C c. 0.86 C d. 0.99 C Carrow_forward1). Determine the equivalent capacitance of the combination shown when C = 12 pF. +11/20 2C C Carrow_forward3). When a capacitor has a charge of magnitude 80 μC on each plate the potential difference across the plates is 16 V. How much energy is stored in this capacitor when the potential difference across its plates is 42 V? a. 1.0 mJ b. 4.4 mJ c. 3.2 mJ d. 1.4 mJ e. 1.7 mJarrow_forward
- 5). A conductor of radius r, length & and resistivity p has resistance R. It is melted down and formed into a new conductor, also cylindrical, with one fourth the length of the original conductor. The resistance of the new conductor is a. 1 R 161 b. 1 R C. R d. 4R e. 16Rarrow_forward8). Determine the magnitude and sense (direction) of the current in the 10-Q2 resistor when I = 1.8 A. 30 V L 50 V 10 Ω 20 Ω a. 1.6 A right to left b. 1.6 A left to right C. 1.2 A right to left d. 1.2 A left to right e. 1.8 A left to right R PGarrow_forward7). Determine the current in the 10-V emf. 5.0 0 w 10 V 5.0 0 15 V 5.0 Ω a. 2.3 A b. 2.7 A c. 1.3 A d. 0.30 A e. 2.5 Aarrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





