Chapter 29, Problem 1P

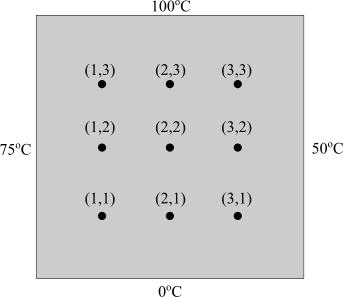
Use Liebmann's method to solve for the temperature of the square heated plate in Fig. 29.4, but with the upper boundary condition increased to $150°\text{C}$ and the left boundary insulated. Use a relaxation factor of 1.2 and iterate to ${\epsilon }_S=1\%$.

To determine

To calculate: The temperature of the square heated plate in the provided figure by Liebmann’s method with the upper boundary condition increased to $150°\text{C}$ and the left boundary insulated;with the use of a relaxation factor of $1.2$ and with iteration to ${\epsilon }_s=1\%$.

Answer to Problem 1P

Solution:

The temperature of the square heated plate is,

$0°\text{C}\underset{0°\text{C}}{\overset{150°\text{C}}{\boxed{\begin{array}{l}67.8609 \text{8}8.3949 85.7155\\ 33.0467 \text{5}0.0069 \text{54}.\text{4659}\\ 14.2989 24.1186 32.1467 \end{array}}}}50°\text{C}$

Explanation of Solution

Given information:

The upper boundary condition increased to $150°\text{C}$ and the left boundary insulated and with the use of a relaxation factor of $1.2$ and with iteration to ${\epsilon }_s=1\%$. The provided figure is,

Calculation:

The following formula is used to calculate the temperature at $\left(i,j\right)$ node as,

$T_{i,j}=\frac{T_{i+1,j}+T_{i-1,j}+T_{i,j+1}+T_{i,j-1}}{4}$

And the percent relative errors is,

$\left|{\left({\epsilon }_a\right)}_{i,j}\right|=\left|\frac{T_{i,j}^{\text{new}}-T_{i,j}^{\text{old}}}{T_{i,j}^{\text{new}}}\right|100\%$

With the help of the above formula, the following code implements the procedure of Liebmann’s method to solve for the temperatures on the platewith the given conditions, that is, theleft boundary is insulated and the upper boundary raised to $150°\text{C}$(from the previous 100 °C). The code can be written with the following script in MATLAB:

Code:

clear;

% initial boundary conditions are given

T =zeros(5);

T(:,1)=0;% left boundary condition

T(5,:)=150;% upper boundary condition

T(:,5)=50;% right boundary condition

T(1,:)=0;% bottom boundary condition

% relaxation and error threshold are defined

lambda =1.2;

epsilon =0.01;

% error matrix definition is given.

errors =ones(3);

iter=0;

whilemax(errors(:))> epsilon

for j =2:4

fori=2:4

Told = T(i,j);

% compute new T at (i, j)

T(i,j)=0.25*(T(i+1,j)+T(i-1,j)+T(i,j+1)+T(i,j-1));

% apply overrelaxation

Tnew= lambda*T(i,j)+(1-lambda)*Told;

T(i,j)=Tnew;

% compute error

errors(i-1,j-1)= abs(Tnew- Told)/abs(Tnew);

end

end

% print result values with iteration

iter=iter+1;

T(2:4,2:4)

maximun_ea=max(errors(:))*100;

disp(maximun_ea)

% print maximum error

end

Output:

On executing the above script, the program finds the stopping condition on the seventh iteration with a maximum error of 0.5169%.

From the above output, the final result can be shown as:

$0°\text{C}\underset{0°\text{C}}{\overset{150°\text{C}}{\boxed{\begin{array}{l}67.8609 \text{8}8.3949 85.7155\\ 33.0467 \text{5}0.0069 \text{54}.\text{4659}\\ 14.2989 24.1186 32.1467 \end{array}}}}50°\text{C}$

And the maximum Error is $0.\text{5169}$.