
Concept explainers
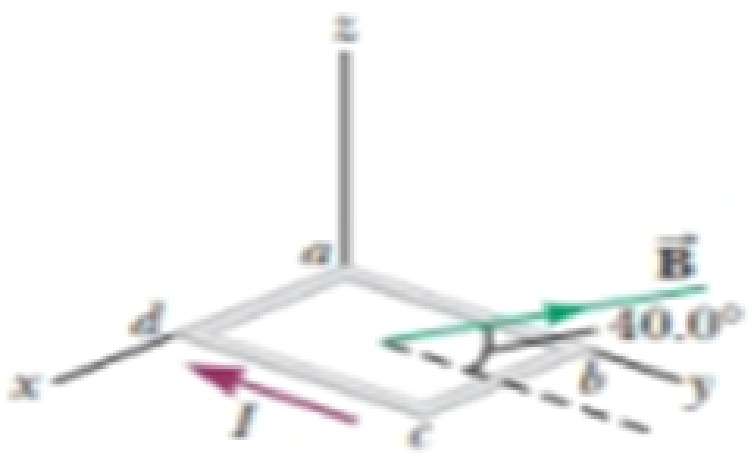
A rectangular loop of wire has dimensions 0.500 m by 0.300 m. The loop is pivoted at the x axis and lies in the xy plane as shown in Figure P28.34. A uniform magnetic field of magnitude 1.50 T is directed at an angle of 40.0° with respect to the y axis with field lines parallel to the yz plane. The loop carries a current of 0.900 A in the direction shown. (Ignore gravitation.) We wish to evaluate the torque on the current loop. (a) What is the direction of the magnetic force exerted on wire segment ab? (b) What is the direction of the torque associated with this force about an axis through the origin? (c) What is the direction of the magnetic force exerted on segment cd? (d) What is the direction of the torque associated with this force about an axis through the origin? (e) Can the forces examined in parts (a) and (c) combine to cause the Loop to rotate around the x axis? (f) Can they affect the motion of the loop in any way? Explain. (g) What is the direction of the magnetic force exerted on segment bc? (h) What is the direction of the torque associated with this force about an axis through the origin? (i) What is the torque on segment ad about an axis through the origin? (j) From the point of view of Figure P28.34, once the loop is released from rest at the position shown, will it rotate clockwise or counterclockwise around the x axis? (k) Compute the magnitude of the magnetic moment of the loop. (l) What is the angle between the magnetic moment sector and the magnetic field? (m) Compute the torque on the loop using the results to parts (k) and (l).
Figure P28.34
(a)
The direction of the magnetic force exerted on wire segment
Answer to Problem 34P
The direction of the force is in the positive x-axis.
Explanation of Solution
Given Info: The length of the rectangular loop is
According to the Fleming left hand rule, if a thumb, an index finger and a middle finger of a right hand is stretch in a position that they formed mutually perpendicular to each other, there the direction of thumb will indicate the direction of force, the direction of index finger will indicate the direction of magnetic field and the direction of middle finger will indicate the direction of current.
By using the Fleming left hand rule, if the middle finger shows the direction of current in segment
Conclusion:
Therefore, the direction of the force is in the positive x-axis.
(b)
The direction of the torque associated with the above force about an axis through the origin.
Answer to Problem 34P
The direction of the torque associated with the force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
Here,
Substitute
The torque associated in the above expression in the negative of the unit vector
Conclusion:
Therefore, the direction of the torque associated with the force on segment
(c)
The direction of the magnetic force exerted on the segment
Answer to Problem 34P
The direction of the magnetic force exerted on the segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the magnetic force on the wire segment
Here,
Substitute
In the above expression it is shown that the magnetic force is in the negative of the unit vector
Conclusion:
Therefore, the direction of the magnetic force exerted on the segment
(d)
The direction of the torque associated with the force on the segment
Answer to Problem 34P
The direction of the torque associated with the force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
Here,
Substitute
The torque associated in the above expression is in the negative of the unit vector
Conclusion:
Therefore, the direction of the torque associated with the force on segment
(e)
Whether the force examined in part (a) and (c) combine to cause the loop to rotate around the x-axis.
Answer to Problem 34P
The magnetic force cannot rotate the loop.
Explanation of Solution
Given Info: The length of the rectangular loop is
As the force examined on the segment
Thus the net force on the rectangular loop become zero.
Conclusion:
Therefore, the magnetic force cannot rotate the loop.
(f)
Whether the above forces affect the motion of the loop.
Answer to Problem 34P
The magnetic force will only rotate the loop and will not affect the motion of the loop.
Explanation of Solution
Given Info: The length of the rectangular loop is
According to the expression in the equation (2) if the magnetic field, current and the length of the loop is constant then its magnetic force will be constant too. In the given problem the magnetic field, the current and the length of the loop is constant, therefore, the magnetic force is constant. Hence this magnetic force will only rotate the loop and will not affect the motion of the loop.
Conclusion:
Therefore, the magnetic force will only rotate the loop and will not affect the motion of the loop.
(g)
The direction of the magnetic force exerted on segment
Answer to Problem 34P
The magnetic force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the magnetic force on the wire segment
Here,
Substitute
In the above expression it is shown that the magnetic force is in the negative of the unit vector
Conclusion:
Therefore, the magnetic force on segment
(h)
The direction of the torque associated with the force on the segment
Answer to Problem 34P
The direction of the torque associated with the force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
Here,
Substitute
The torque associated in the above expression is in the positive of the unit vector
Conclusion:
Therefore, the direction of the torque associated with the force on segment
(i)
The direction of the torque on the segment
Answer to Problem 34P
The torque on the segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
The segment
Conclusion:
Therefore, the torque on the segment
(j)
Whether the loop locate itself clockwise or anticlockwise.
Answer to Problem 34P
The rectangular loop will rotate in the anticlockwise direction.
Explanation of Solution
Given Info: The length of the rectangular loop is
As the torque on the segment
Conclusion:
Therefore, the rectangular loop will rotate in the anticlockwise direction.
(k)
The magnitude of the magnetic moment of the loop.
Answer to Problem 34P
The magnitude of the magnetic moment of the loop is
Explanation of Solution
Given Info: The length of the rectangular loop is
The formula to calculate the magnetic moment of the loop is,
Here,
Substitute
Conclusion:
Therefore, the magnitude of the magnetic moment of the loop is
(l)
The angle between the magnetic moment vector and magnetic field.
Answer to Problem 34P
The angle between the magnetic moment and magnetic field is
Explanation of Solution
Given Info: The length of the rectangular loop is
It is given that the current if lowing in clockwise direction therefore, here follow the principle of right hand thumb rule, if the finger is curl in the direction of current then the thumb will indicate the moment of magnetic field. Thus, the direction of magnetic moment is downward. That is along the negative z direction. The angle between the magnetic moment and magnetic field is,
Conclusion:
Therefore, the angle between the magnetic moment and magnetic field is
(m)
The torque on the loop using the results of part (k) and (l).
Answer to Problem 34P
The torque on the loop is
Explanation of Solution
Given Info: The length of the rectangular loop is
Formula to calculate the torque in current carrying wire is,
Substitute
Conclusion:
Therefore, the torque on the loop is
Want to see more full solutions like this?
Chapter 28 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Multi-term
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Fundamentals Of Thermodynamics
MARINE BIOLOGY
Genetics: From Genes to Genomes
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
- The shear leg derrick is used to haul the 200-kg net of fish onto the dock as shown in. Assume the force in each leg acts along its axis. 5.6 m. 4 m- B Part A Determine the compressive force along leg AB. Express your answer to three significant figures and include the appropriate units. FAB = Value Submit Request Answer Part B Units ? Determine the compressive force along leg CB. Express your answer to three significant figures and include the appropriate units. FCB= Value Submit Request Answer Part C ? Units Determine the tension in the winch cable DB. Express your answer with the appropriate units. 2marrow_forwardPart A (Figure 1) shows a bucket suspended from a cable by means of a small pulley at C. If the bucket and its contents have a mass of 10 kg, determine the location of the pulley for equilibrium. The cable is 6 m long. Express your answer to three significant figures and include the appropriate units. Figure 4 m B НА x = Value Submit Request Answer Provide Feedback < 1 of 1 T 1 m Units ?arrow_forwardThe particle in is in equilibrium and F4 = 165 lb. Part A Determine the magnitude of F1. Express your answer in pounds to three significant figures. ΑΣΦ tvec F₁ = Submit Request Answer Part B Determine the magnitude of F2. Express your answer in pounds to three significant figures. ΑΣΦ It vec F2 = Submit Request Answer Part C Determine the magnitude of F3. Express your answer in pounds to three significant figures. ? ? lb lb F₂ 225 lb 135° 45° 30° -60°-arrow_forward
- The 10-lb weight is supported by the cord AC and roller and by the spring that has a stiffness of k = 10 lb/in. and an unstretched length of 12 in. as shown in. Part A Determine the distance d to maintain equilibrium. Express your answer in inches to three significant figures. 節 ΕΠΙ ΑΣΦ d = *k J vec 5 t 0 ? d C A in. 12 in. Barrow_forwardThe members of a truss are connected to the gusset plate as shown in . The forces are concurrent at point O. Take = 90° and T₁ = 7.5 kN. Part A Determine the magnitude of F for equilibrium. Express your answer to three significant figures and include the appropriate units. F = Value Submit Request Answer Part B 0 ? Units Determine the magnitude of T2 for equilibrium. Express your answer to three significant figures and include the appropriate units. ? T₂ = Value Units T₁ Carrow_forwardpls help on botharrow_forward
- pls helparrow_forwardpls helparrow_forward6. 6. There are 1000 turns on the primary side of a transformer and 200 turns on thesecondary side. If 440 V are supplied to the primary winding, what is the voltageinduced in the secondary winding? Is this a step-up or step-down transformer? 7. 80 V are supplied to the primary winding of a transformer that has 50 turns. If thesecondary side has 50,000 turns, what is the voltage induced on the secondary side?Is this a step-up or step-down transformer? 8. There are 50 turns on the primary side of a transformer and 500 turns on thesecondary side. The current through the primary winding is 6 A. What is the turnsratio of this transformer? What is the current, in milliamps, through the secondarywinding?9. The current through the primary winding on a transformer is 5 A. There are 1000turns on the primary winding and 20 turns on the secondary winding. What is theturns ratio of this transformer? What is the current, in amps, through the secondarywinding?arrow_forward
- No chatgpt plsarrow_forwardWhat is the current, in amps, across a conductor that has a resistance of10 Ω and a voltage of 20 V? 2. A conductor draws a current of 100 A and a resistance of 5 Ω. What is thevoltageacross the conductor? 3. What is the resistance, in ohm’s, of a conductor that has a voltage of 80 kVand acurrent of 200 mA? 4. An x-ray imaging system that draws a current of 90 A is supplied with 220V. What is the power consumed? 5. An x-ray is produced using 800 mA and 100 kV. What is the powerconsumed in kilowatts?arrow_forwardՍՈՈՒ XVirginia Western Community Coll x P Course Home X + astering.pearson.com/?courseld=13289599#/ Figure y (mm) x=0x = 0.0900 m All ✓ Correct For either the time for one full cycle is 0.040 s; this is the period. Part C - ON You are told that the two points x = 0 and x = 0.0900 m are within one wavelength of each other. If the wave is moving in the +x-direction, determine the wavelength. Express your answer to two significant figures and include the appropriate units. 0 t(s) λ = Value m 0.01 0.03 0.05 0.07 Copyright © 2025 Pearson Education Inc. All rights reserved. 日 F3 F4 F5 1775 % F6 F7 B F8 Submit Previous Answers Request Answer ? × Incorrect; Try Again; 3 attempts remaining | Terms of Use | Privacy Policy | Permissions | Contact Us | Cookie Settings 28°F Clear 4 9:23 PM 1/20/2025 F9 prt sc F10 home F11 end F12 insert delete 6 7 29 & * ( 8 9 0 t = back Οarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





