
(a)
To make a
(a)
Answer to Problem 28.14AYK
The strongest
Explanation of Solution
In the question, it is given that experimenters assessed the concentration of lactic acid, acetic acid and hydrogen sulfide in thirty randomly chosen pieces of cheddar cheese. The table is given which shows the data. The scatterplot with taste on the y axis is as follows:
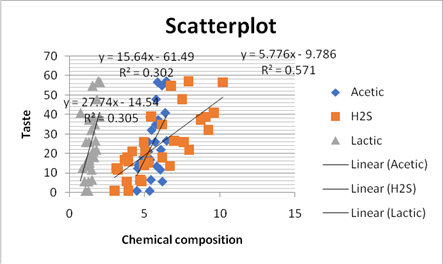
As we can see in the scatterplot that all the lines are almost parallel and also that the R -square of the hydrogen sulfide is largest with taste so the correlation is largest for the hydrogen sulfide. The correlation is given in the scatterplot above by finding square root, the calculation is as:
| Acetic | =SQRT(0.302) |
| Lactic | =SQRT(0.3055) |
| H2S | =SQRT(0.5712) |
And the result is as:
| Acetic | 0.549545 |
| Lactic | 0.552721 |
| H2S | 0.755778 |
(b)
To use a software to obtain the regression equation and run inference for a regression model that includes all three explanatory variables and interpret the software output, including the meaning of the value taken by
(b)
Answer to Problem 28.14AYK
The equation is
Explanation of Solution
In the question, it is given that experimenters assessed the concentration of lactic acid, acetic acid and hydrogen sulfide in thirty randomly chosen pieces of cheddar cheese. The table is given which shows the data. Now, run inference for a regression model that includes all three explanatory variables and interpret the software output by using the Excel, the result will be as:
| Regression Statistics | |
| Multiple R | 0.800438 |
| R Square | 0.640701 |
| Adjusted R Square | 0.599243 |
| Standard Error | 10.29053 |
| Observations | 30 |
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 3 | 4909.619 | 1636.54 | 15.45438 | 5.68E-06 |
| Residual | 26 | 2753.268 | 105.8949 | ||
| Total | 29 | 7662.887 |
| Coefficients | Standard Error | t Stat | P-value | |
| Intercept | -32.8566 | 20.2335 | -1.62387 | 0.116466 |
| Acetic | 2.000654 | 4.346475 | 0.460294 | 0.649132 |
| H2S | 4.566348 | 1.176917 | 3.879925 | 0.000639 |
| Lactic | 13.67117 | 6.643259 | 2.057902 | 0.049755 |
And the equation is as:
And
(c)
To explain which explanatory variable does it describe and create a new regression model that excludes this explanatory variable and interpret the software output and compare it with your findings in (b).
(c)
Answer to Problem 28.14AYK
That explanatory variable is Acetic.
Explanation of Solution
In the question, it is given that experimenters assessed the concentration of lactic acid, acetic acid and hydrogen sulfide in thirty randomly chosen pieces of cheddar cheese. The table is given which shows the data. In the above result in part (b), we can see that the explanatory variable Acetic has a P-value greater than the level of significance so it is not significant. Thus, we will remove this variable and run this test with the other two variables using Excel and the result will be as:
| Regression Statistics | |
| Multiple R | 0.798607 |
| R Square | 0.637773 |
| Adjusted R Square | 0.610941 |
| Standard Error | 10.13922 |
| Observations | 30 |
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 2 | 4887.183 | 2443.592 | 23.76946 | 1.11E-06 |
| Residual | 27 | 2775.704 | 102.8038 | ||
| Total | 29 | 7662.887 |
| Coefficients | Standard Error | t Stat | P-value | |
| Intercept | -24.4609 | 8.629104 | -2.8347 | 0.008581 |
| H2S | 4.858662 | 0.976305 | 4.976581 | 3.24E-05 |
| Lactic | 14.28672 | 6.411593 | 2.228263 | 0.034385 |
In this all the explanatory variables are statistically significant but in the above model in (b) all are not statistically significant but the variations explained are approximately equal.
(d)
To explain which explanatory variable of the two has the less significant or larger value and create a new regression model that excludes this explanatory variable and keeps only significant one and explain how does this last model compare with the model in (c).
(d)
Answer to Problem 28.14AYK
The explanatory variable of the two has the less significant or larger value is lactic.
Explanation of Solution
In the question, it is given that experimenters assessed the concentration of lactic acid, acetic acid and hydrogen sulfide in thirty randomly chosen pieces of cheddar cheese. The table is given which shows the data. In the above result in part (c), we can see that the P-value for the Lactic is larger than the hydrogen sulfide thus, we will remove the Lactic variable and then run the
| Regression Statistics | |
| Multiple R | 0.755752 |
| R Square | 0.571162 |
| Adjusted R Square | 0.555846 |
| Standard Error | 10.83338 |
| Observations | 30 |
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 1 | 4376.746 | 4376.746 | 37.29265 | 1.37E-06 |
| Residual | 28 | 3286.141 | 117.3622 | ||
| Total | 29 | 7662.887 |
| Coefficients | Standard Error | t Stat | P-value | |
| Intercept | -9.78684 | 5.95791 | -1.64266 | 0.111638 |
| H2S | 5.776089 | 0.94585 | 6.10677 | 1.37E-06 |
In this as we compare it with the model in part (c), we can see that the coefficient of determination or the variations explained are less in this model then in part (c) and all the slopes are statistically significant.
(e)
To explain which model best explains cheddar taste and check the conditions for inference for this model and conclude.
(e)
Answer to Problem 28.14AYK
Model (b) best explains cheddar taste and conditions are met.
Explanation of Solution
In the question, it is given that experimenters assessed the concentration of lactic acid, acetic acid and hydrogen sulfide in thirty randomly chosen pieces of cheddar cheese. The table is given which shows the data. By looking at the model (b), (c) and (d), we can say that the variations explained is more in part (b) than in (c) and (d). Thus, the model in (b) best explains cheddar taste. The conditions for inferences are as: as we can see in the scatterplot, it shows the linearity and as we look at the data it shows the normality and constant variance by looking at the model regression analysis using Excel’s residual plot and the data is randomly selected so it shows independence. Thus, the conditions are met.
Want to see more full solutions like this?
Chapter 28 Solutions
Practice of Statistics in the Life Sciences
- This problem is based on the fundamental option pricing formula for the continuous-time model developed in class, namely the value at time 0 of an option with maturity T and payoff F is given by: We consider the two options below: Fo= -rT = e Eq[F]. 1 A. An option with which you must buy a share of stock at expiration T = 1 for strike price K = So. B. An option with which you must buy a share of stock at expiration T = 1 for strike price K given by T K = T St dt. (Note that both options can have negative payoffs.) We use the continuous-time Black- Scholes model to price these options. Assume that the interest rate on the money market is r. (a) Using the fundamental option pricing formula, find the price of option A. (Hint: use the martingale properties developed in the lectures for the stock price process in order to calculate the expectations.) (b) Using the fundamental option pricing formula, find the price of option B. (c) Assuming the interest rate is very small (r ~0), use Taylor…arrow_forwardDiscuss and explain in the picturearrow_forwardBob and Teresa each collect their own samples to test the same hypothesis. Bob’s p-value turns out to be 0.05, and Teresa’s turns out to be 0.01. Why don’t Bob and Teresa get the same p-values? Who has stronger evidence against the null hypothesis: Bob or Teresa?arrow_forward
- Review a classmate's Main Post. 1. State if you agree or disagree with the choices made for additional analysis that can be done beyond the frequency table. 2. Choose a measure of central tendency (mean, median, mode) that you would like to compute with the data beyond the frequency table. Complete either a or b below. a. Explain how that analysis can help you understand the data better. b. If you are currently unable to do that analysis, what do you think you could do to make it possible? If you do not think you can do anything, explain why it is not possible.arrow_forward0|0|0|0 - Consider the time series X₁ and Y₁ = (I – B)² (I – B³)Xt. What transformations were performed on Xt to obtain Yt? seasonal difference of order 2 simple difference of order 5 seasonal difference of order 1 seasonal difference of order 5 simple difference of order 2arrow_forwardCalculate the 90% confidence interval for the population mean difference using the data in the attached image. I need to see where I went wrong.arrow_forward
- Microsoft Excel snapshot for random sampling: Also note the formula used for the last column 02 x✓ fx =INDEX(5852:58551, RANK(C2, $C$2:$C$51)) A B 1 No. States 2 1 ALABAMA Rand No. 0.925957526 3 2 ALASKA 0.372999976 4 3 ARIZONA 0.941323044 5 4 ARKANSAS 0.071266381 Random Sample CALIFORNIA NORTH CAROLINA ARKANSAS WASHINGTON G7 Microsoft Excel snapshot for systematic sampling: xfx INDEX(SD52:50551, F7) A B E F G 1 No. States Rand No. Random Sample population 50 2 1 ALABAMA 0.5296685 NEW HAMPSHIRE sample 10 3 2 ALASKA 0.4493186 OKLAHOMA k 5 4 3 ARIZONA 0.707914 KANSAS 5 4 ARKANSAS 0.4831379 NORTH DAKOTA 6 5 CALIFORNIA 0.7277162 INDIANA Random Sample Sample Name 7 6 COLORADO 0.5865002 MISSISSIPPI 8 7:ONNECTICU 0.7640596 ILLINOIS 9 8 DELAWARE 0.5783029 MISSOURI 525 10 15 INDIANA MARYLAND COLORADOarrow_forwardSuppose the Internal Revenue Service reported that the mean tax refund for the year 2022 was $3401. Assume the standard deviation is $82.5 and that the amounts refunded follow a normal probability distribution. Solve the following three parts? (For the answer to question 14, 15, and 16, start with making a bell curve. Identify on the bell curve where is mean, X, and area(s) to be determined. 1.What percent of the refunds are more than $3,500? 2. What percent of the refunds are more than $3500 but less than $3579? 3. What percent of the refunds are more than $3325 but less than $3579?arrow_forwardA normal distribution has a mean of 50 and a standard deviation of 4. Solve the following three parts? 1. Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the answer of the second part.) 2. Compute the probability of a value greater than 55.0. Use the same formula, x=55 and subtract the answer from 1. 3. Compute the probability of a value between 52.0 and 55.0. (The question requires finding probability value between 52 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 52, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…arrow_forward
- If a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by a step by step creating a chart. Clearly mark the range, identifying the…arrow_forwardClient 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127arrow_forwardClient 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127 a) Determine the mean change in patient weight from before to after the diet (after – before). What is the 95% confidence interval of this mean difference?arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





