
Concept explainers
A parallel-plate capacitor has square plates of side s = 2.50 cm and plate separation d = 2.50 mm. The capacitor is charged by a battery to a charge Q = 4.00 μC, after which the battery is disconnected. A porcelain dielectric (κ = 6.5) is then inserted a distance y = 1.00 cm into the capacitor (Fig. P27.88). Hint: Consider the system as two capacitors connected in parallel. a. What is the effective capacitance of this capacitor? b. How much energy is stored in the capacitor? c. What are the magnitude and direction of the force exerted on the dielectric by the plates of the capacitor?
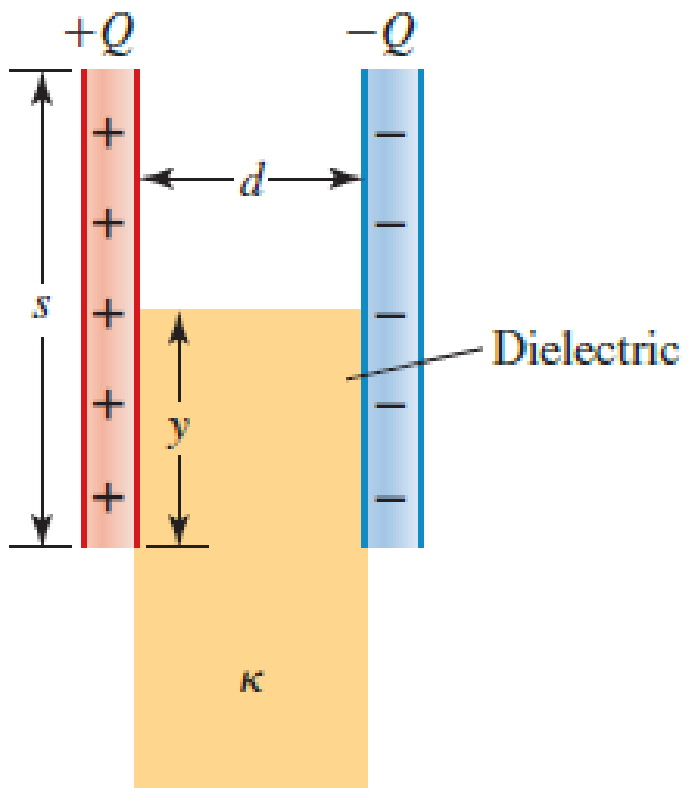
Figure P27.88
(a)
Effective capacitance of the capacitor.
Answer to Problem 88PQ
Effective capacitance of the capacitor is
Explanation of Solution
Write the expression to find the capacitance of the parallel plate capacitor with dielectric.
Here,
Substitute
Write the expression to find the capacitance of the parallel plate which is unfilled.
Here,
Substitute
The system can be considered as two capacitors are connected in parallel.
Write the expression to find the equivalent capacitance of the two capacitors connected in parallel.
Here,
Conclusion:
Substitute
Therefore, effective capacitance of the capacitor is
(b)
The energy stored in the capacitor.
Answer to Problem 88PQ
The energy stored in the capacitor is
Explanation of Solution
Write the expression to find the equivalent capacitance of the two capacitors connected in parallel.
Here,
Substitute equations (I) and (II) in above expression to find the equivalent capacitance
Write the equation for energy stored in the capacitor.
Here,
Substitute equation (III) in above expression to find the energy stored in the capacitor.
Conclusion:
Substitute
Therefore, the energy stored in the capacitor is
(c)
The magnitude and direction of the force exerted on dielectric by the plates of capacitor.
Answer to Problem 88PQ
The magnitude and direction of the force exerted on dielectric by the plates of capacitor is
Explanation of Solution
Write the equation for energy stored in the capacitor.
Here,
Substitute equation (III) in above expression to find the energy stored in the capacitor.
Write the expression to find the force exerted on dielectric by the plates of capacitor.
Substitute equation (IV) in above expression to find the force exerted on dielectric by the plates of capacitor.
Conclusion:
Substitute
Therefore, the magnitude and direction of the force exerted on dielectric by the plates of capacitor is
Want to see more full solutions like this?
Chapter 27 Solutions
EBK WEBASSIGN FOR KATZ'S PHYSICS FOR SC
- Gas is compressed in a cylinder creating 31 Joules of work on the gas during the isothermal process. How much heat flows from the gas into the cylinder in Joules?arrow_forwardThe heat engine gives 1100 Joules of energy of high temperature from the burning gasoline by exhausting 750 Joules to low-temperature . What is the efficiency of this heat engine in a percentage?arrow_forwardL₁ D₁ L₂ D2 Aluminum has a resistivity of p = 2.65 × 10 8 2. m. An aluminum wire is L = 2.00 m long and has a circular cross section that is not constant. The diameter of the wire is D₁ = 0.17 mm for a length of L₁ = 0.500 m and a diameter of D2 = 0.24 mm for the rest of the length. a) What is the resistance of this wire? R = Hint A potential difference of AV = 1.40 V is applied across the wire. b) What is the magnitude of the current density in the thin part of the wire? Hint J1 = c) What is the magnitude of the current density in the thick part of the wire? J₂ = d) What is the magnitude of the electric field in the thin part of the wire? E1 = Hint e) What is the magnitude of the electric field in the thick part of the wire? E2 =arrow_forward
- please helparrow_forwardA cheetah spots a gazelle in the distance and begins to sprint from rest, accelerating uniformly at a rate of 8.00 m/s^2 for 5 seconds. After 5 seconds, the cheetah sees that the gazelle has escaped to safety, so it begins to decelerate uniformly at 6.00 m/s^2 until it comes to a stop.arrow_forwardA projectile is fired with an initial speed of 40.2 m/s at an angle of 35.0 degree above the horizontal on a long flat firing range. Determine. please help and show work for them so i can understand.arrow_forward
- pls helparrow_forwardJ K L The graph in the figure shows the position of an object as a function of time. The letters H-L represent particular moments of time. At which moments shown (H, I, etc.) is the speed of the object the greatest? + Position H I K Timearrow_forward1. Two pendula of slightly different length oscillate next to each other. The short one oscillates with frequency 0.52 Hz and the longer one with frequency 0.50 Hz. If they start of in phase determine their phase difference after 75 s.arrow_forward
- A mass is connect to a vertical revolving axle by two strings of length L, each making an angle of 45 degrees with the axle, as shown. Both the axle and mass are revolving with angular velocity w, Gravity is directed downward. The tension in the upper string is T_upper and the tension in the lower string is T_lower.Draw a clear free body diagram for mass m. Please include real forces only.Find the tensions in the upper and lower strings, T_upper and T_lowerarrow_forward2. A stone is dropped into a pool of water causing ripple to spread out. After 10 s the circumference of the ripple is 20 m. Calculate the velocity of the wave.arrow_forward10. Imagine you have a system in which you have 54 grams of ice. You can melt this ice and then vaporize it all at 0 C. The melting and vaporization are done reversibly into a balloon held at a pressure of 0.250 bar. Here are some facts about water you may wish to know. The density of liquid water at 0 C is 1 g/cm³. The density of ice at 0 C is 0.917 g/cm³. The enthalpy of vaporization of liquid water is 2.496 kJ/gram and the enthalpy of fusion of solid water is 333.55 J/gram. A. How much energy does the ice absorb as heat when it melts? B. How much work is involved in melting the ice? C. What is the total change in energy for melting the ice? D. What is the enthalpy change for melting the ice? E. What is the entropy change for melting the ice? F. What is the change in Helmholtz energy for melting the ice? G. What is the change in Gibbs energy for melting the ice?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





