Calculus Volume 2
2nd Edition
ISBN: 9781630182021
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax College.
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2.6, Problem 2SP
The Grand Canyon Skywalk opened to the public on March 28, 2007. This engineering marvel is a horseshoe-shaped observation platform suspended 4000 ft above the Colorado River on the West Rim of the Grand Canyon. Its crystal-clear glass floor allows stunning views of the canyon below (see the following figure).
The Skywalk is a cantilever design, meaning that the observation platform extends over the rim of the canyon, with no visible means of support below it. Despite the lack of visible support posts or struts, cantilever structures are engineered to be very stable and the Skywalk is no exception. The observation platform is attached firmly to support posts that extend 46 ft down into bedrock. The structure was built to withstand 100-mph winds and an 8.0-magnitude earthquake within 50 mi, and is capable of supporting more than 70,000,000 lb.
One factor affecting the stability of the Skywalk is the center of gravity of the structure. We are going to calculate the center of gravity of the Skywalk, and examine how the center of gravity changes when tourists walk out onto the observation platform.
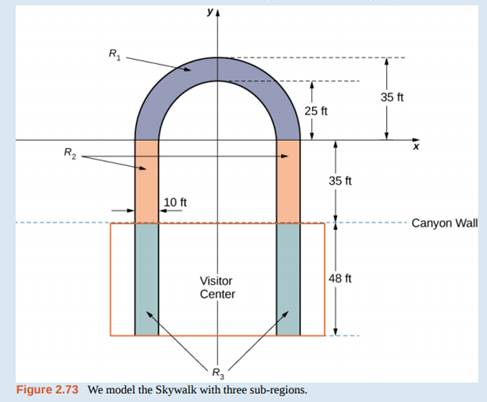
The observation platform is U-shaped. The legs of the U are 10 ft wide and begin on land, under the visitors' center, 48 ft from the edge of the canyon. The platform extends 70 ft over the edge of the canyon.
To calculate the center of mass of the structure, we treat it as a lamina and use a two-dimensional region in the xy-plane to represent the platform. We begin by dividing the region into three subregions so we can consider each subregion separately. The first region, denoted R1, consists of the curved part of the U. We model R1as a semicircular annulus, with inner radius 25 ft and outer radius 35 ft, centered at the origin (see the following figure).
The legs of the platform, extending 35 ft between R1and the canyon wall, comprise the second sub-region, R2, Last, the ends of the legs, which extend 48 ft under the visitor center, comprise the third sub-region, R3. Assume the density of the lamina is constant and assume the total weight of the platform is 1,200,000 lb (not including the weight of the visitor center; we will consider that later). Use g = 32 ft/sec2.
2.Determine the mass associated with each of the three sub-regions.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Find the limit. (If the limit is infinite, enter 'oo' or '-o', as appropriate. If the limit does not otherwise exist, enter DNE.)
lim
X→ ∞
(✓
81x2
-
81x + x
9x)
Please solve the following Statistics and Probability Problem (show all work) :
The probability that a patient recovers from a rare blood disease is 0.4 and 10 people are known to havecontracted this disease. Let X denote the random variable which denotes the number of patient who survivefrom the disease.1. Plot the probability mass function (pmf) of X.2. Plot the cumulative distribution function (cdf) of X.3. What is the probability that at least 8 survive, i.e., P {X ≥ 8}?4. What is the probability that 3 to 8 survive, i.e., P {3 ≤ X ≤ 8}?
think about what you know about measurements. fill in each box. use words, numbers, and pictures. Show as many ideas as you can.
Chapter 2 Solutions
Calculus Volume 2
Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, split the region...Ch. 2.1 - For the following exercises, split the region...Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...
Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - The largest triangle with a base on the x- axis...Ch. 2.1 - A factory selling cell phones has a marginal cost...Ch. 2.1 - An amusement park has a marginal cost function...Ch. 2.1 - The tortoise versus the hare: The speed of the...Ch. 2.1 - The tortoise versus the hare: The speed of the...Ch. 2.1 - For the following exercises, find the area between...Ch. 2.1 - For the following exercises, find the area between...Ch. 2.1 - For the following exercises, find the area between...Ch. 2.1 - For the following exercises, solve using calculus,...Ch. 2.1 - For the following exercises, solve using calculus,...Ch. 2.2 - Derive the formula for the volume of a sphere...Ch. 2.2 - Use the slicing method to derive the formula for...Ch. 2.2 - Use the slicing method to derive the formula for...Ch. 2.2 - Use the disk method to derive the formula for the...Ch. 2.2 - Explain when you would use the disk method versus...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - Yogurt containers can be shaped like frustums....Ch. 2.2 - Rotate the ellipse (x2/a2)+(y2/b2)=1 around the...Ch. 2.2 - Rotate the ellipse (x2/a2)+(y2/b2)=1 around the...Ch. 2.2 - A better approximation of the volume of a football...Ch. 2.2 - What is the volume of the Bundt cake that comes...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - Consider the region enclosed by the graphs of y =...Ch. 2.3 - Consider the function y=f(x), which decreases from...Ch. 2.4 - For the following exercises, find the Length of...Ch. 2.4 - For the following exercises, find the Length of...Ch. 2.4 - For the following exercises, find the Length of...Ch. 2.4 - Pick an arbitrary linear function x = g(y) over...Ch. 2.4 - Find the surface area of the volume generated when...Ch. 2.4 - Find the surface area of the volume generated when...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - The base of a lamp is constructed by revolving a...Ch. 2.4 - [T] A lampshade is constructed by rotating y =1/x...Ch. 2.4 - [T] An anchor drags behind a boat according to the...Ch. 2.4 - [T] You are building a bridge that will span 10...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - Find the generalized center of mass in the sliver...Ch. 2.6 - Find the generalized center of mass between y =...Ch. 2.6 - Find the generalized center of mass between y = b...Ch. 2.6 - Use the theorem of Pappus to find the volume of a...Ch. 2.6 - Find the center of mass (x,y) for a thin wire...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the indefinite...Ch. 2.7 - For the following exercises, find the indefinite...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - Find the area of the hyperbolic quarter-circle...Ch. 2.7 - If you are unable to find intersection points...Ch. 2.7 - If you are unable to find intersection points...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - For the following exercises, use y=y0ekt . 352.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 353.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 354.How...Ch. 2.8 - For the following exercises, use y=y0ekt . 355. If...Ch. 2.8 - For the following exercises, use y=y0ekt . 356....Ch. 2.8 - For the following exercises, use y=y0ekt . 357.The...Ch. 2.8 - For the following exercises, use y=y0ekt ....Ch. 2.8 - For the following exercises, use y=y0ekt . 359....Ch. 2.8 - For the following exercises, use y=y0ekt . 360.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 361.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 362. If...Ch. 2.8 - For the following exercises, use y=y0ekt ....Ch. 2.8 - For the following exercises, use y=y0ekt . 364.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 365.You...Ch. 2.8 - For the following exercises, use y=y0ekt . 366.You...Ch. 2.8 - For the following exercises, use y=y0ekt . 367.You...Ch. 2.8 - For the following exercises, use y=y0ekt . 368....Ch. 2.8 - For the following exercises, use y=y0ekt . 369....Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.9 - [T] Find expressions for cosh x + sinh x and cosh...Ch. 2.9 - From the definitions of cosh(x) and sinh(x), find...Ch. 2.9 - Show that cosh(x) and sinh(x) satisfy y" = y.Ch. 2.9 - Use the quotient rule to verify that tanh(x)' =...Ch. 2.9 - Derive cosh2(x) + sinh2(x) = cosh(2x) from the...Ch. 2.9 - Take the derivative of the previous expression to...Ch. 2.9 - Prove sinh(x + y) = sinh(x)cosh(y) +...Ch. 2.9 - Take the derivative of the previous expression to...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, use the fact that a...Ch. 2.9 - For the following exercises, use the fact that a...Ch. 2.9 - For the following exercises, use the fact that a...Ch. 2.9 - For the following exercises, use this scenario: A...Ch. 2.9 - For the following exercises, use this scenario: A...Ch. 2.9 - For the following exercises, use this scenario: A...Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find the requested...Ch. 2 - For the following exercises, find the requested...Ch. 2 - For the following exercises, find the surface area...Ch. 2 - For the following exercises, find the surface area...Ch. 2 - For the following exercises, consider the Karun-3...Ch. 2 - For the following exercises, consider the Karun-3...Ch. 2 - For the following exercise, consider the stock...Ch. 2 - For the following exercises, consider the...Ch. 2 - For the following exercises, consider the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
29-36. Total and Annual Returns. Compute the total and annual returns on the following investments.
29. Five ye...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
ASSESSMENT Each of the following sequences is either arithmetic or geometric. Identify the sequences 230,193+82...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Twenty five people, consisting of 15 women and 10 men are lined up in a random order. Find the probability that...
A First Course in Probability (10th Edition)
Version 2 of the Chain Rule Use Version 2 of the Chain Rule to calculate the derivatives of the following funct...
Calculus: Early Transcendentals (2nd Edition)
Evaluate the integrals in Exercises 17–66.
23.
University Calculus: Early Transcendentals (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Please solve the following Probability and Statistics problem (show all work and double check solution is correct): Suppose that a die is rolled twice. What are the possible values that the following random variables can take1. the maximum value to appear in the two rolls;2. the value of the first roll minus the value of the second roll?3. Calculate the probabilities associated with the above two random variables?arrow_forwardPlease solve the following statistics and probability problem (show all work) : This problem is to show that determining if two events are independent is not always obvious.1. Consider a family of 3 children. Consider the following two events. A is the event that the familyhas children of both sexes and B is the event that there is at most one girl. Are events A and Bindependent?2. What is the answer in a family with 4 children?arrow_forwardPlease solve the following Probability and Statistics problems: (show all work) Suppose that a die is rolled twice. What are the possible values that the following random variables can take1. the maximum value to appear in the two rolls;2. the value of the first roll minus the value of the second roll?3. Calculate the probabilities associated with the above two random variables?arrow_forward
- Please solve the following Statistics and Probability Problem (show all work) : The probability that a patient recovers from a rare blood disease is 0.4 and 10 people are known to havecontracted this disease. Let X denote the random variable which denotes the number of patient who survivefrom the disease.1. Plot the probability mass function (pmf) of X.2. Plot the cumulative distribution function (cdf) of X.3. What is the probability that at least 8 survive, i.e., P {X ≥ 8}?4. What is the probability that 3 to 8 survive, i.e., P {3 ≤ X ≤ 8}?arrow_forward2) Compute the following anti-derivative. √1x4 dxarrow_forwardPlease solve the following Probability and Statistics problem (please double check solution and provide explanation): A binary communication channel carries data as one of two types of signals denoted by 0 and 1. Owing tonoise, a transmitted 0 is sometimes received as a 1 and a transmitted 1 is sometimes received as a 0. For agiven channel, assume a probability of 0.94 that a transmitted 0 is correctly received as a 0 and a probability0.91 that a transmitted 1 is received as a 1. Further assume a probability of 0.45 of transmitting a 0. If asignal is sent, determine 1. Probability that a 1 is received2. Probability that a 0 is received3. Probability that a 1 was transmitted given that a 1 was received4. Probability that a 0 was transmitted given that a 0 was received5. Probability of an errorarrow_forward
- 1) Compute the inverse of the following matrix. 0 1 1 A = 5 1 -1 2-3 -3arrow_forwardQuestion 3 (5pt): A chemical reaction. In an elementary chemical reaction, single molecules of two reactants A and B form a molecule of the product C : ABC. The law of mass action states that the rate of reaction is proportional to the product of the concentrations of A and B: d[C] dt = k[A][B] (where k is a constant positive number). Thus, if the initial concentrations are [A] = = a moles/L and [B] = b moles/L we write x = [C], then we have (E): dx dt = k(ax)(b-x) 1 (a) Write the differential equation (E) with separate variables, i.e. of the form f(x)dx = g(t)dt. (b) Assume first that a b. Show that 1 1 1 1 = (a - x) (b - x) - a) a - x b - x b) (c) Find an antiderivative for the function f(x) = (a-x) (b-x) using the previous question. (d) Solve the differentiel equation (E), i.e. find x as a function of t. Use the fact that the initial concentration of C is 0. (e) Now assume that a = b. Find x(t) assuming that a = b. How does this expression for x(t) simplify if it is known that [C] =…arrow_forward2) Consider the matrix M = [1 2 3 4 5 0 2 3 4 5 00345 0 0 0 4 5 0 0 0 0 5 Determine whether the following statements are True or False. A) M is invertible. B) If R5 and Mx = x, then x = 0. C) The last row of M² is [0 0 0 0 25]. D) M can be transformed into the 5 × 5 identity matrix by a sequence of elementary row operations. E) det (M) 120 =arrow_forward
- 3) Find an equation of the plane containing (0,0,0) and perpendicular to the line of intersection of the planes x + y + z = 3 and x y + z = 5. -arrow_forward3) Find the volume of the solid that lies inside both the sphere x² + y² + z² cylinder x²+y² = 1. = 4 and thearrow_forward1) In the xy-plane, what type of conic section is given by the equation - √√√(x − 1)² + (y − 1)² + √√√(x + 1)² + (y + 1)² : - = 3?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Hypothesis Testing using Confidence Interval Approach; Author: BUM2413 Applied Statistics UMP;https://www.youtube.com/watch?v=Hq1l3e9pLyY;License: Standard YouTube License, CC-BY
Hypothesis Testing - Difference of Two Means - Student's -Distribution & Normal Distribution; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=UcZwyzwWU7o;License: Standard Youtube License