Chapter 25, Problem 83P

(a)

To determine

The diagram of the circuit.

Answer to Problem 83P

The diagram is shown in figure (1).

Explanation of Solution

Calculation:

The diagram of the electric circuit is shown below,

  

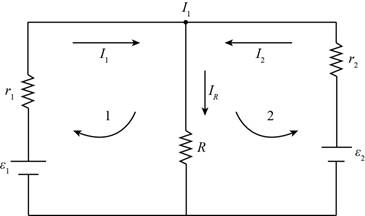
Figure (1)

Conclusion:

Therefore, the diagram is shown in figure (1).

(b)

To determine

The current in each branch of the circuit.

Answer to Problem 83P

The current $I_1$ , $I_2$ and $I_{\text{R}}$ are $-30.0\text{A}$ , $36.45\text{A}$ and $6.45\text{A}$ respectively.

Explanation of Solution

Formula used:

The expression for Kirchhoff’s law in first loop is given by,

  ${\epsilon }_1-I_1{r}_1-I_{\text{R}}R=0$

The expression for Kirchhoff’s law in second loop is given by,

  ${\epsilon }_2-I_2{r}_2-I_{\text{R}}R=0$

The expression for current in loop 1 is given by,

  $I_1+I_2=I_{\text{R}}$

Calculation:

The expression for Kirchhoff’s law in first loop is calculated as,

  $\begin{array}{c}{\epsilon }_1-I_1{r}_1-I_{\text{R}}R=0\\ \left(11.4\text{V}\right)-I_1\left(50\text{mΩ}\right)-I_{\text{R}}\left(2\Omega \right)=0\\ \left(11.4\text{V}\right)-I_1\left(\left(50\text{mΩ}\right)\left(\frac{1\Omega }{{10}^3\text{mΩ}}\right)\right)-\left(I_1+I_2\right)\left(2.0\text{Ω}\right)=0\\ I_1\left(2.05\text{Ω}\right)+I_2\left(2.0\text{Ω}\right)=11.4\text{V}\end{array}$ …… (1)

The expression for Kirchhoff’s law in second loop is calculated as,

  $\begin{array}{c}{\epsilon }_2-I_2{r}_2-I_{\text{R}}R=0\\ \left(12.6\text{V}\right)-I_1\left(10\text{mΩ}\right)-I_{\text{R}}\left(2\Omega \right)=0\\ \left(12.6\text{V}\right)-I_1\left(\left(10\text{mΩ}\right)\left(\frac{{10}^{-3}\Omega }{1\text{mΩ}}\right)\right)-\left(I_1+I_2\right)\left(2\Omega \right)=0\\ I_1\left(2.01\text{Ω}\right)+I_2\left(2.0\text{Ω}\right)=12.6\text{V}\end{array}$ …… (2)

From equation (1) and (2),

  $\begin{array}{c}{I}_1\left(0.04\text{Ω}\right)=-1.2\text{V}\\ I_1=-30\text{A}\end{array}$

Substitute $-30\text{A}$ for $I_1$ in equation (1).

  $\begin{array}{c}\left(-30.0\text{A}\right)\left(2.05\text{Ω}\right)+I_2\left(2.0\text{Ω}\right)=11.4\text{V}\\ I_2\left(2.0\text{Ω}\right)=72.9\text{V}\\ I_2=36.45\text{A}\end{array}$

The $I_{\text{R}}$ is calculated as,

  $\begin{array}{c}{I}_{\text{R}}=I_1+I_2\\ =-30.0\text{A}+36.45\text{A}\\ =6.45\text{A}\end{array}$

Conclusion:

Therefore, the current $I_1$ , $I_2$ and $I_{\text{R}}$ are $-30.0\text{A}$ , $36.45\text{A}$ and $6.45\text{A}$ respectively.

(c)

To determine

The power supplied by second battery.

Answer to Problem 83P

The power supplied by second battery is $445.98\text{W}$ .

Explanation of Solution

Formula used:

The expression for power received by first battery is given by,

  $P_1=\left({\epsilon }_1+I_1{r}_1\right)I_1$

The expression for power received by second battery is given by,

  $P_2=\left({\epsilon }_2-I_2{r}_2\right)I_2$

The expression for power dissipated in load resistance is given by,

  $P_{\text{R}}=I_{\text{R}}^{2}R$

Calculation:

The expression for power received by first battery is calculated as,

  $\begin{array}{c}{P}_1=\left({\epsilon }_1+I_1{r}_1\right)I_1\\ =\left(11.4\text{V}+\left(-30.0\text{A}\right)\left(\left(50\text{mΩ}\right)\left(\frac{{10}^{-3}\text{Ω}}{1\text{mΩ}}\right)\right)\right)\left(-30.0\text{A}\right)\\ =-297\text{W}\end{array}$

The expression for power received by second battery is calculated as,

  $\begin{array}{c}{P}_2=\left({\epsilon }_2-I_2{r}_2\right)I_2\\ =\left(12.6\text{V}-\left(36.45\text{A}\right)\left(\left(10\text{mΩ}\right)\left(\frac{{10}^{-3}\text{Ω}}{1\text{mΩ}}\right)\right)\right)\left(36.45\text{A}\right)\\ =445.98\text{W}\end{array}$

The power dissipated in load resistance is calculated as,

  $\begin{array}{c}{P}_{\text{R}}=I_{\text{R}}^{2}R\\ ={\left(6.45\text{A}\right)}^2\left(2.0\Omega \right)\\ =83.21\text{W}\end{array}$

Conclusion:

Therefore, the power supplied by second battery is $445.98\text{W}$ .