
Concept explainers
(a)
The proof for
(a)
Answer to Problem 71CP
The electric potential at the point
Explanation of Solution
The following figure shows the diagram of the dipoles and the point
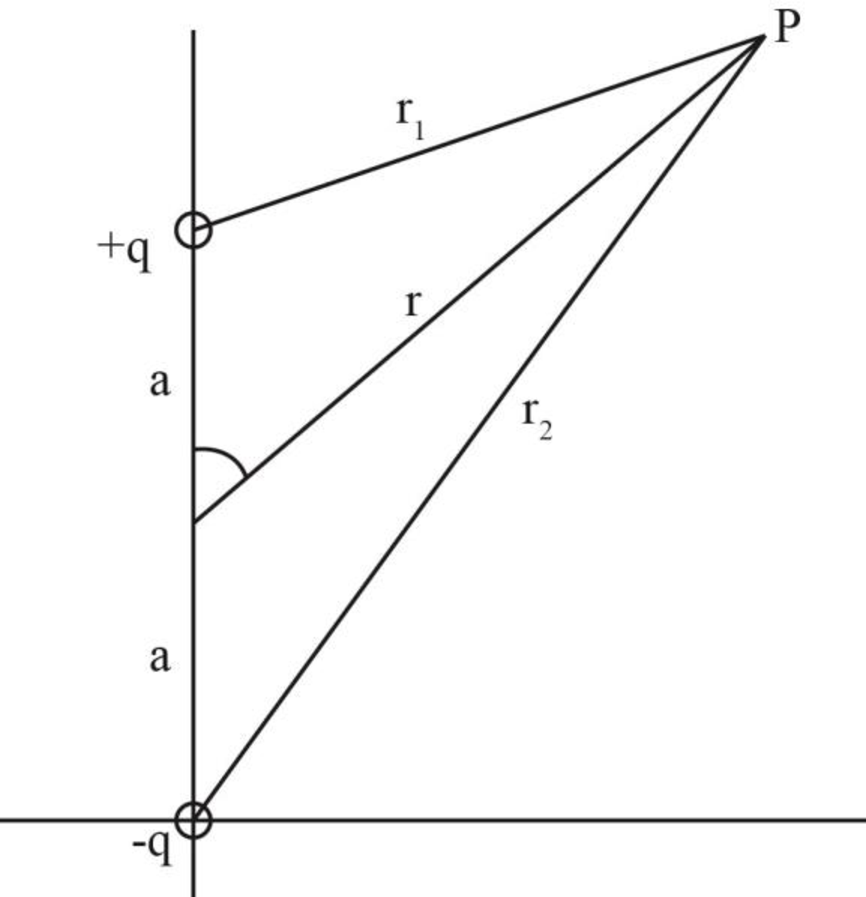
Figure-(1)
The dipole moment’s magnitude is given as.
Here,
Write the equation for the electric potential at the point
Here,
Write the equation for the distance between the positive charge and the point
Write the equation for the distance between the negative charge and the point
Rearrange the equation (II) and (III) to calculate
Expand the above equation binomially and neglect the higher terms to calculate
Substitute
Substitute
Therefore, the electric potential at the point
(b)
The electric field’s radial component
(b)
Answer to Problem 71CP
The electric field’s radial component is
Explanation of Solution
Write the equation for the radial component of the electric field.
Here,
Write the equation for the perpendicular component of the electric field.
Here,
Conclusion:
Substitute
Substitute
Therefore, the electric field’s radial component is
(c)
Whether the results for
(c)
Answer to Problem 71CP
Yes, the results for
Explanation of Solution
Write the equation for
Write the equation for
Conclusion:
Substitute
Substitute
Substitute
Substitute
Therefore, the results for
(d)
Whether the results for
(d)
Answer to Problem 71CP
No, the results for
Explanation of Solution
Write the equation for
Write the equation for
Conclusion:
Substitute
Substitute
Therefore, the results for
(e)
The expression for the electric potential in terms of the Cartesian coordinates.
(e)
Answer to Problem 71CP
The expression for the electric potential in terms of the Cartesian coordinates is
Explanation of Solution
Write the equation for the electric potential.
Conclusion:
Substitute
Therefore, the expression for the electric potential in terms of the Cartesian coordinates is
(f)
The
(f)
Answer to Problem 71CP
The
Explanation of Solution
Write the equation for the
Here,
Write the equation for the
Here,
Conclusion:
Substitute
Substitute
Therefore, the
Want to see more full solutions like this?
Chapter 25 Solutions
Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
- No chatgpt plsarrow_forwardCar A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B, will be 2 μF A 1 µF B 3 µFarrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed. NOT AI PLSarrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardPlease don't use Chatgpt will upvote and give handwritten solutionarrow_forward
- No chatgpt pls will upvote Already got wrong chatgpt answerarrow_forwardAn electron and a proton are each accelerated through a potential difference of 21.0 million volts. Find the momentum (in MeV/c) and the kinetic energy (in MeV) of each, and compare with the results of using the classical formulas. Momentum (MeV/c) relativistic classical electron proton Kinetic Energy (MeV)arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 20.0 µF.) (a) Find the equivalent capacitance between points a and b. µF (b) Calculate the charge on each capacitor, taking ΔVab = 14.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





