
Concept explainers
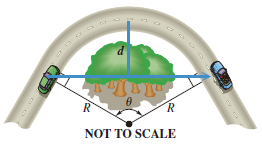
(Modeling) Stopping Distance on a Curve Refer to Exercise 43. When an automobile travels along a circular curve, objects like trees and buildings situated on the inside of the curve can obstruct the driver's vision. These obstructions prevent the driver from seeing sufficiently far down the highway to ensure a safe stopping distance. In the figure, the minimum distance d that should be cleared on the inside of the highway is modeled by the equation
(Source: Mannering. F. and W. Kilareski. Principles of Highway Engineering and
Traffic Analysis, Second Edition. John Wiley and Sons.)
(a) It can be shown that if θ is measured in degrees, then
(b) Compute d to the nearest foot for a 65 mph speed limit given S = 485 ft and R = 600 ft.
(c) How does the speed limit affect the amount of land that should be cleared on the inside of the curve?
Reference Exercise:
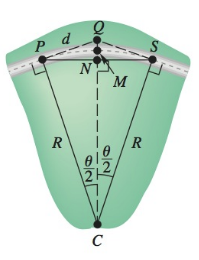
(Modeling) Highway Curves A basic highway curve connecting two straight sections of road may be circular. In the figure, the points P and S mark the beginning and end of the curve. Let be the point of intersection where the two straight sections of highway leading into the curve would meet if extended. The radius of the curve is R, and the central
Principles of Highway Engineering and Traffic Analysis, Second Edition, John Wiley and Sons.)
(a) If R = 965 ft and θ = 37°, find the distance d between P and Q.
(b) Find an expression in terms of R and θ for the distance between points M and N.
Want to see the full answer?
Check out a sample textbook solution
Chapter 2 Solutions
Trigonometry (11th Edition)
- Question 10 (5 points) (07.04 MC) Vectors u and v are shown in the graph. -12-11 -10 -9 -8 -7 -6 -5 What is proju? a -6.5i - 4.55j b -5.2i+2.6j с -4.7631 3.334j d -3.81i+1.905j < + 10 6 5 4 3 2 -3 -2 -10 1 -1 -2 -3 u -4 -5 -6 -7arrow_forwardFind the lengths of PR and OR in terms of the angles α and β. Find the angles ∠ONQ and ∠NPQ. Find the lengths of ON and PN in terms of the angle β. Find the length of PQ. Find the length of QR. Find the length of OM. Find the length of RM. What formula can you write down by noting that PR = QR + PQ? What formula can you write down by noting that OR = OM - RM?arrow_forward5) Solve the triangle. 2 95° 4 B с A) c=3.63, A=59.5°, B = 25.5° C) c = 4.63, A = 59.5°, B = 25.5° A B) c 4.63, A 25.5°, B = 59.5° = = D) c 5.63, A = 25.5°, B = 59.5°arrow_forward
- Find zw. Leave your answer in polar form. = လ 3π 2 z = 6 cos 6 cos 37 3π + i sin 2 57 W = 12 cos + i sin 6 6 ༠།ལྦ་arrow_forward10 Write the expression (1 – i) i)in the standard form a + bi.arrow_forward11) The letters r and 0 represent polar coordinates. Write the equation r sine = 10 using rectangular coordinates (x, y). A) x = 10y B) y = 10 C) x = 10 D) y = 10xarrow_forward
- 18) Find all the complex cube roots of - 8i. Leave your answers in polar form with the argument in degrees.arrow_forwardWrite the complex number √3 - i in polar form.arrow_forward2 10) The letters x and y represent rectangular coordinates. Write the equation x² + 4y = 4 using polar coordinates (r, e). A) 4 cos² 0 + sin² 0 = 4r C) r²(4 cos² 0 + sin² 0) = 4 B) cos² 0 + 4 sin² 0 = 4r D) r² (cos20 + 4 sin² 0) = 4arrow_forward
- 2) A radio transmission tower is 130 feet tall. How long should a guy wire be if it is to be attached 6 feet from the top and is to make an angle of 20° with the ground? Give your answer to the nearest tenth of a foot.arrow_forward4) Two sides and an angle are given. Determine whether the given information results in one triangle, two triangles, or no triangle at all. Solve any triangle(s) that results. b=6, c=7, B = 80° A) one triangle B=40°, A = 60°, a = 13 C) one triangle C 39°, A 61°, a = 15 = B) one triangle C=41°, A = 59°, a = 17 D) no trianglearrow_forward7) A painter needs to cover a triangular region 63 meters by 67 meters by 74 meters. A can of paint covers 70 square meters. How many cans will be needed?arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL  Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning




