Chapter 2.5, Problem 42E

(Modeling) Distance of a Shot Put A shot-putter trying to improve performance may wonder whether there is an optimal angle to aim for, or whether the velocity (speed) at which the ball is thrown is more important. The figure shows the path of a steel ball thrown by a shot-putter. The distance D depends on initial velocity v, height h. and angle θ when the ball is released.

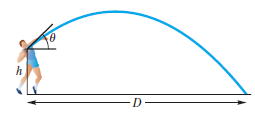
One model developed for this situation gives D as

$D=\frac{v^2\sin \theta \cos \theta +v\cos \theta \sqrt{{\left(v\sin \theta \right)}^2+64h}}{32}.$

Typical ranges for the variables are v: 33-46 ft per sec: h: 6-8 ft; and θ: 40°-45°.

(Source: Kreighbaum. E. and K. Barthels, Biomechanics, Allyn & Bacon.)

(a) To see how angle θ affects distance D. let v = 44 ft per sec and h = 7 ft. Calculate D. to the nearest hundredth, for θ = 40°. 42°, and 45°. How does distance D change as θ increases?

(b) To see how velocity v affects distance D, let h = 7 and θ = 42°. Calculate D, to the nearest hundredth, for v = 43, 44. and 45 ft per sec. How does distance D change as v increases?

(c) Which affects distance D more, v or θ? What should the shot-putter do to improve performance?