Chapter 25, Problem 2P

Solve the following problem over the interval from $x=0\text{ to 1}$ using a step size of 0.25 where $y\left(0\right)=1$. Display all your results on the same graph.

$\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$

(a) Analytically.

(b) Euler's method.

(c) Heun's method without iteration.

(d) Ralston's method.

(e) Fourth-order RK method.

To determine

To calculate: The solution of the initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$ with initial condition as $y\left(0\right)=1$, analytically.

Answer to Problem 2P

Solution: The solution to the initial value problem is $y\left(t\right)={\left(\frac{2t^2+t+2}{2}\right)}^2$.

Explanation of Solution

Given Information:

The initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$ with $y\left(0\right)=1$.

Formula used:

To solvean initial value problem of the form $\frac{dy}{dx}=g\left(x\right)h\left(y\right)$ integrate both sides of the following equation:

$\frac{dy}{h\left(y\right)}=g\left(x\right)dx$

Calculation:

Rewrite the provided differential equation as,

$\begin{array}{c}\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}\\ \frac{dy}{\sqrt{y}}=\left(1+4t\right)dt\end{array}$

Integrate both sides to get,

$\begin{array}{c}2y^{\frac{1}{2}}=t+2t^2+C\\ y\left(t\right)={\left(\frac{t+2t^2+C}{2}\right)}^2\end{array}$

Now use the initial condition $y\left(0\right)=1$ to get the value of the constant C.

$\begin{array}{c}y\left(0\right)={\left(\frac{0+2{\left(0\right)}^2+C}{2}\right)}^2\\ 1=\frac{C^2}{4}\\ C=2\end{array}$

Hence, the analytical solution of the initial value problem is $y\left(t\right)={\left(\frac{t+2t^2+2}{2}\right)}^2$.

To determine

To calculate: The solution of the initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$ with initial condition as $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ and the step-size of $0.25$ using the Euler’s method.

Answer to Problem 2P

Solution: For $h=0.25$ the values are,

t	y
0	1
0.25	1.25
0.5	1.809017
0.75	2.817765
1	4.496385

Explanation of Solution

Given Information:

The initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$, with $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ with step-size 0.25.

Formula used:

Solvean initial value problem of the form $\frac{dy}{dx}=f\left(x_i,y_i\right)$ using the iterative Euler method as,

$y_{i+1}=y_i+f\left(x_i,y_i\right)h$

Calculation:

From the initial condition $y\left(0\right)=1$, $y_0=1,t_0=0$.

Thus, evaluate the function $f\left(t_0,y_0\right)$ as,

$\begin{array}{c}f\left(1,0\right)=\left(1+4\left(0\right)\right)\sqrt{1}\\ =1\end{array}$

Further,

$\begin{array}{c}{y}_1=y_0+f\left(y_0,t_0\right)h\\ y\left(0.25\right)=y\left(0\right)+f\left(1,0\right)0.25\\ =1+1\left(0.25\right)\\ =1.25\end{array}$

Proceed further and use the following MATLAB code to implement Euler’s method and solve the differential equation.

% Q 2 (b) Euler's Method when h=0.25

clear;clc;

% Define the end-points of the interval [0,2]

a=0;b=1;

% Define the initial condition y(0)=1

y1(1)=1;

t1(1)=a;

dydt1(1)=1;

% Mention the step-size as 0.25

h1=0.25;

% Compute the value of the number of iterations corresponding to the step-size;

n1=(b-a)/h1;

% Start the loop for the Euler's method

fori=1:n1

% Compute the value of the function to the right of the

% differential equation

dydt1(i+1)=(1+4*t1(i))*sqrt(y1(i));

% Compute the value of the variable y

y1(i+1)=y1(i)+h1*dydt1(i+1);

% Compute the value of the variable t

t1(i+1)=t1(i)+h1;

end

A1=[t1;y1]'

Execute the above code to obtain the solutions stored in matrix $A1$ as,

A1 =

0 1.0000

0.2500 1.2500

0.5000 1.8090

0.7500 2.8178

1.0000 4.4964

The results thus obtained are tabulated as,

T	y
0	1
0.25	1.25
0.5	1.809017
0.75	2.817765
1	4.496385

To determine

To calculate: The solution of the initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$ with initial condition as $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ with step-size 0.25 using the Heun’s methodwithout iteration.

Answer to Problem 2P

Solution: The solutions are tabulated as,

$\begin{array}{cccc}t& y& k_1& k_2\\ 0& 1& 1& 1.25\\ 0.25& 1.404508& 2.370239& 4.23953\\ 0.5& 2.3703& 4.480688& 7.322187\\ 0.75& 3.706089& 7.70482& 11.86508\\ 1& 6.151785& 12.4014& 18.52039\end{array}$

Explanation of Solution

Given Information:

The initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$, with $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ with step-size of 0.25.

Formula used:

Solve an initial value problem of the form $\frac{dy}{dx}=f\left(x_i,y_i\right)$ using the Heun’s method without iteration as,

$y_{i+1}=y_i+\left(\frac{k_1+k_2}{2}\right)h$

In the above expression,

$\begin{array}{l}{k}_1=f\left(k_i,y_i\right)\\ k_2=f\left(x_i+h,y_i+k_{1}h\right)\end{array}$

Calculation:

From the initial condition $y\left(0\right)=1$, $y_0=1,t_0=0$.

Thus, evaluate the function $f\left(t_0,y_0\right)$ as,

$\begin{array}{c}{k}_1=f\left(1,0\right)\\ =\left(1+4\left(0\right)\right)\sqrt{1}\\ =1\end{array}$

And,

$\begin{array}{c}{k}_2=f\left(t_0+0.25,y_0+1\left(0.25\right)\right)\\ =f\left(0.25,1.25\right)\\ =2.236068\end{array}$

Thus,

$\begin{array}{c}{y}_1=y_0+\left(\frac{k_1+k_2}{2}\right)h\\ =1+\left(\frac{1+2.236068}{2}\right)0.25\\ =1.404508\end{array}$

Proceed further and use the following MATLAB code to implement Heun’s method and solve the differential equation.

% ———————————–

% Q 2 (c) Heun's Method when h=0.25

% Define the end-points of the interval [0,2]

a=0;b=1;

% Define the initial condition y(0)=1

y2(1)=1;

t2(1)=a;

dydt2(1)=1;

% Mention the step-size as 0.25

h2=0.25;

% Compute the value of the number of iterations corresponding to the step-size;

n2=(b-a)/h2;

% Start the loop for the Heun's method

fori = 1:n2+1

k21(i) = (1+4*t2(i))*sqrt(y2(i));

k22(i) = (1+4*(t2(i)+h2))*sqrt(y2(i)+k21(i)*h2);

y2(i+1) = y2(i) + 0.5*h2*(k21(i)+k22(i));

t2(i+1) = t2(i) + h2;

end

t2(:, end:end)=[];

y2(:, end:end)=[];

A2=[t2; y2; k21; k22]'

Execute the above code to obtain the solutions stored in matrix $A2$ as,

A2 =

0 1.0000 1.0000 2.2361

0.2500 1.4045 2.3702 4.2395

0.5000 2.2307 4.4807 7.3222

0.7500 3.7061 7.7005 11.8651

1.0000 6.1518 12.4014 18.2504

Theresults thus obtained aretabulated as,

$\begin{array}{cccc}t& y& k_1& k_2\\ 0& 1& 1& 1.25\\ 0.25& 1.404508& 2.370239& 4.23953\\ 0.5& 2.3703& 4.480688& 7.322187\\ 0.75& 3.706089& 7.70482& 11.86508\\ 1& 6.151785& 12.4014& 18.25039\end{array}$

To determine

To calculate: The solution of the initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$ with $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ with step-size 0.25 using the Ralston’s method without iteration.

Answer to Problem 2P

Solution: The solutions are tabulated as,

$\begin{array}{cccc}t& y& k_1& k_2\\ 0& 1& 1& 1.907018\\ 0.25& 1.40117& 2.36742& 3.735408\\ 0.5& 2.221023& 4.470929& 6.559094\\ 0.75& 3.686783& 7.680398& 10.75522\\ 1& 6.119352& 12.36866& 16.70321\end{array}$

Explanation of Solution

Given Information:

The initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$, with $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ and with the step-size of 0.25.

Formula used:

Solve an initial value problem of the form $\frac{dy}{dx}=f\left(x_i,y_i\right)$ using the Ralston’s method without iteration as,

$y_{i+1}=y_i+\left(\frac{k_1+2k_2}{3}\right)h$

In the above expression,

$\begin{array}{l}{k}_1=f\left(k_i,y_i\right)\\ k_2=f\left(x_i+\frac{3}{4}h,y_i+\frac{3}{4}{k}_{1}h\right)\end{array}$

Calculation:

From the initial condition $y\left(0\right)=1$, $y_0=1,t_0=0$.

Thus, evaluate the function $f\left(t_0,y_0\right)$ as,

$\begin{array}{c}{k}_1=f\left(1,0\right)\\ =\left(1+4\left(0\right)\right)\sqrt{1}\\ =1\end{array}$

And,

$\begin{array}{c}{k}_2=f\left(t_0+\frac{3}{4}\left(0.25\right),y_0+\frac{3}{4}\left(1\right)\left(0.25\right)\right)\\ =f\left(0.1875,1.1875\right)\\ =1.907078\end{array}$

Thus,

$\begin{array}{c}{y}_1=y_0+\left(\frac{k_1+2k_2}{3}\right)h\\ =1+\left(\frac{1+2\left(1.907018\right)}{3}\right)0.25\\ =1.40117\end{array}$

Proceed further and use the following MATLAB code to implement Ralston’s method and solve the differential equation.

% —————————————–

% Q 2 (d) Ralston's Method when h=0.25

% Define the end-points of the interval [0,2]

a=0;b=1;

% Define the initial condition y(0)=1

y3(1)=1;

t3(1)=a;

dydt3(1)=1;

% Mention the step-size as =0.25

h3=0.25;

% Compute the value of the number of iterations corresponding to the step-size;

n3=(b-a)/h3;

% Start the loop for the Heun's method

fori = 1:n3+1

k31(i) = (1+4*t3(i))*sqrt(y3(i));

k32(i) = (1+4*(t3(i)+0.75*h3))*sqrt(y3(i)+k31(i)*0.75*h3);

y3(i+1) = y3(i) + (1/3)*h3*(k31(i)+2*k32(i));

t3(i+1) = t3(i) + h3;

end

t3(:, end:end)=[];

y3(:, end:end)=[];

A3=[t3; y3; k31; k32]'

Execute the above code to obtain the solutions stored in matrix $A3$ as,

A3 =

0 1.0000 1.0000 1.9070

0.2500 1.4012 2.3674 3.7354

0.5000 2.2210 4.4709 6.5591

0.7500 3.6868 7.6804 10.7552

1.0000 6.1194 12.3687 16.7032

The results thus obtained are tabulated as,

$\begin{array}{cccc}t& y& k_1& k_2\\ 0& 1& 1& 1.907018\\ 0.25& 1.40117& 2.36742& 3.735408\\ 0.5& 2.221023& 4.470929& 6.559094\\ 0.75& 3.686783& 7.680398& 10.75522\\ 1& 6.119352& 12.36866& 16.70321\end{array}$

To determine

To calculate: The solution of the initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$ with $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ with step-size 0.25 using the RK method of order four.

Answer to Problem 2P

Solution: The solutions are tabulated as,

$\begin{array}{cccccc}t& y& k_1& k_2& k_3& k_4\\ 0& 1& 1& 1.59099& 1.642396& 2.375373\\ 0.25& 1.410089& 2.374944& 3.266264& 3.371176& 4.502883\\ 0.5& 2.249786& 4.499786& 5.869427& 6.045447& 7.757471\\ 0.75& 3.753411& 7.749489& 9.778674& 10.09787& 12.51287\\ 1& 6.249054& 12.49905& 15.37192& 15.72129& 19.14308\end{array}$

Explanation of Solution

Given Information:

The initial value problem $\frac{dy}{dt}=\left(1+4t\right)\sqrt{y}$, with $y\left(0\right)=1$ in the interval $t\in \left(0,1\right)$ and with the step-size of 0.25.

Formula used:

Solve an initial value problem of the form $\frac{dy}{dx}=f\left(x_i,y_i\right)$ using the iterative fourth order RK method as,

$y_{i+1}=y_i+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)h$

In the above expression,

$\begin{array}{c}{k}_1=f\left(x_i,y_i\right)\\ k_2=f\left(x_i+\frac{h}{2},y_i+\frac{h}{2}{k}_1\right)\\ k_3=f\left(x_i+\frac{h}{2},y_i+\frac{h}{2}{k}_2\right)\\ k_4=f\left(x_i+h,y_i+k_{3}h\right)\end{array}$

Calculation:

From the initial condition $y\left(0\right)=1$, $y_0=1,t_0=0$, thus,

$\begin{array}{c}{k}_1=f\left(1,0\right)\\ =\left(1+4\left(0\right)\right)\sqrt{1}\\ =1\end{array}$

Ans,

$\begin{array}{c}{k}_2=f\left(t_0+\frac{0.25}{2},y_0+\left(\frac{0.25}{2}\right)k_1\right)\\ =f\left(0.25,1.125\right)\\ =1.59099\end{array}$

And,

$\begin{array}{c}{k}_3=f\left(t_0+\frac{0.25}{2},y_0+\left(\frac{0.25}{2}\right)k_2\right)\\ =f\left(0.25,1.198874\right)\\ =1.642396\end{array}$

And,

$\begin{array}{c}{k}_4=f\left(t_0+0.25,y_0+0.25k_3\right)\\ =f\left(0.5,1.410599\right)\\ =2.375373\end{array}$

Therefore,

$\begin{array}{c}{y}_1=y_0+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)\left(0.25\right)\\ =1+\frac{1}{6}\left(1+2\left(1.59099\right)+2\left(1.642396\right)+\left(2.375373\right)\right)\left(0.25\right)\\ =1.410089\end{array}$

Proceed further and use the following MATLAB code to implement RK method of order four, solve the differential equation, and compare the results obtained from part (a) to part (e) on a single plot.

% % ————————————————–

% Q 2 (e) RK 4 Method when h=0.25

% Define the end-points of the interval [0,2]

a=0;b=1;

% Define the initial condition y(0)=1

y4(1)=1;

t4(1)=a;

% Mention the step-size as 0.25

h4=0.25;

% Compute the value of the number of iterations corresponding to the step-size;

n4=(b-a)/h4;

halfh = h4 / 2;

h6 = h4/6;

% Start the process

fori = 1: n4+1

t4(i+1) = t4(i) + h4;

% The values usually defined as k1, k2, k3 and k4

s41(i) = (1+4*t4(i))*sqrt(y4(i));

s42(i) = (1+4*(t4(i)+halfh))*sqrt(y4(i)+halfh*s41(i));

s43(i) = (1+4*(t4(i)+halfh))*sqrt(y4(i)+halfh*s42(i));

s44(i) = (1+4*(t4(i)+h4))*sqrt(y4(i)+h4*s43(i));

% The formula for the RK method of order 4

y4(i+1,:) = y4(i,:) + (s41(i) + s42(i)+s42(i) + s43(i)+s43(i) + s44(i)) * h6;

end;

t4(:, end:end)=[];

y4(end:end,:)=[];

% Display the values

A4=[t4' y4 s41' s42' s43' s44']

% Now plot the graphs for all the parts:

time=linspace(0,2);

exactsol=(time.^2+0.5*time+1).^2;

plot(time, exactsol)

xlabel('t')

axis([0 1.25 0 7])

hold on

plot(A1(:,1), A1(:,2));

hold on

plot(A2(:,1), A2(:,2));

hold on

plot(A3(:,1), A3(:,2));

hold on

plot(A4(:,1), A4(:,2));

hold on

legend('y(t)','Euler','Heun','Ralston','RK-4')

Execute the above code to obtain the solutions stored in matrix $A4$ as,

A4 =

0 1.0000 1.0000 1.5910 1.6424 2.3754

0.2500 1.4101 2.3749 3.2663 3.3712 4.5029

0.5000 2.2498 4.4998 5.8694 6.0454 7.7575

0.7500 3.7534 7.7495 9.7787 10.0379 12.5129

1.0000 6.2491 12.4991 15.3719 15.7213 19.1431

The results thus obtained are tabulated as,

$\begin{array}{cccccc}t& y& k_1& k_2& k_3& k_4\\ 0& 1& 1& 1.59099& 1.642396& 2.375373\\ 0.25& 1.410089& 2.374944& 3.266264& 3.371176& 4.502883\\ 0.5& 2.249786& 4.499786& 5.869427& 6.045447& 7.757471\\ 0.75& 3.753411& 7.749489& 9.778674& 10.09787& 12.51287\\ 1& 6.249054& 12.49905& 15.37192& 15.72129& 19.14308\end{array}$

Plot for all the methods along with the analytical solution $y\left(t\right)={\left(\frac{2t^2+t+2}{2}\right)}^2$ is,

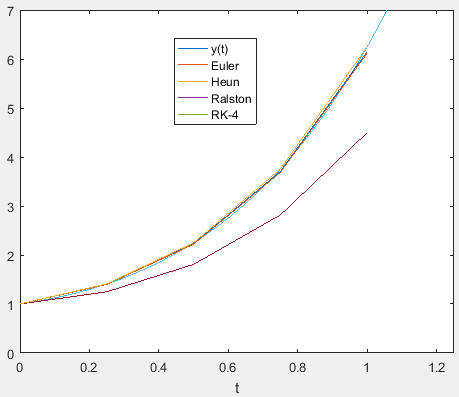
From the graph, it is inferred that the RK method of order 4 is the best approximation to the solution.