
Concept explainers
a.
To test and conclude: Whether there is a relationship between the highest degrees obtained and attended religious services.
a.
Answer to Problem 25.44E
There is sufficient evidence to support the claim that there is a relationship between the highest degrees obtained and attended religious services. That is, the attending religious service has effect on getting degrees.
Explanation of Solution
Given info:
The statement “Did any one attended religious services last week” was asked to randomly selected subjects.
Calculation:
The claim is to test whether there is any relationship between the highest degrees obtained and attended religious services.
Cell frequency for using Chi-square test:
When at most 20% of the cell frequencies are less than 5
If all the individual frequencies are 1 or more than 1.
All the expected frequencies must be 5 or greater than 5
The hypotheses used for testing are given below:
Software procedure:
Software procedure for calculating the chi-square test statistic is given below:
Click on Stat, select Tables and then click on Chi-square Test (Two-way table in a worksheet).
Under Columns containing the table: enter the columns of High School, Junior College, Bachelor, and Graduate.
Click ok.
Output obtained from MINITAB is given below:
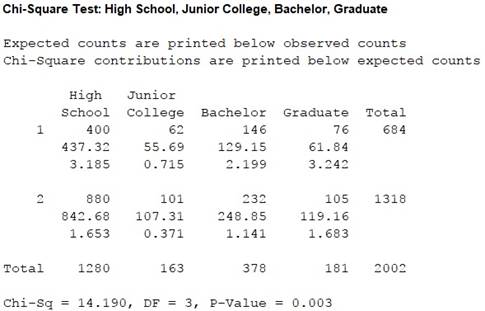
Thus, the test statistic is 14.190, the degree of freedom is 3 and the P-value is 0.003.
Since all the expected frequencies are greater than 5, the usage of chi-square test is appropriate.
Conclusion:
The P-value is 0.003 and level of significance is 0.05.
Thus, the P-value is lesser than the level of significance.
The null hypothesis is rejected.
Thus, there is sufficient evidence to support the claim that there is a relationship between the highest degrees obtained and attended religious services.
b.
To make: A
To test: Whether there is relationship between the types of highest degrees obtained and attended religious services and describes the result.
b.
Answer to Problem 25.44E
The
| Highest degree obtained | |||
| Attended Services | Junior College | Bachelor | Graduate |
| Yes | 62 | 146 | 76 |
| No | 101 | 232 | 105 |
There is no sufficient evidence to support the claim that there is relationship between the types of highest degrees obtained and attended religious services.
The relationship between the types of highest degrees obtained and attended religious services changes.
Explanation of Solution
Calculation:
The claim is to test whether there is any relationship between the types of highest degrees obtained and attended religious services.
The hypotheses used for testing are given below:
Software procedure:
Software procedure for calculating the chi-square test statistic is given below:
- Click on Stat, select Tables and then click on Chi-square Test (Two-way table in a worksheet).
- Under Columns containing the table: enter the columns of Junior College, Bachelor, and Graduate.
- Click ok.
Output obtained from MINITAB is given below:
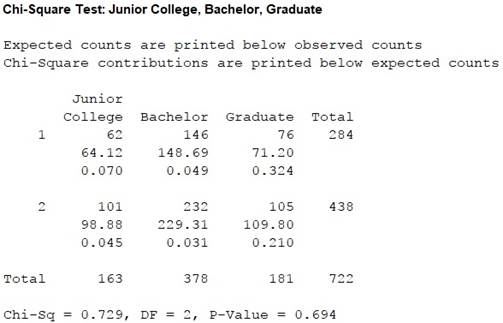
Thus, the test statistic is 0.729, the degree of freedom is 2 and the P-value is 0.694.
Since all the expected frequencies are greater than 5, the usage of chi-square test is appropriate.
Conclusion:
The P-value is 0.694 and level of significance is 0.05
Thus, the P-value is greater than the level of significance.
The null hypothesis is not rejected.
Thus, there is no sufficient evidence to support the claim that there is relationship between the types of highest degrees obtained and attended religious services.
When the High school degree column is omitted, the relationship between the types of highest degrees obtained and attended religious services do not exist.
c.
To make: A
To test: Whether there is relationship between getting a degree beyond high school and attended religious services.
c.
Answer to Problem 25.44E
The
| Highest Degree obtained | ||
| Attended Services | High School | Degrees beyond High School |
| Yes | 62 | 284 |
| No | 101 | 438 |
There is not sufficient evidence to support the claim that there is relationship between getting a degree beyond high school and attended religious services
There is no influence of attending religious services on getting highest degree hold.
Explanation of Solution
Calculation:
A two way table by adding the columns of “Junior School”, “Bachelor” and “Graduate” is given below:
| Highest Degree obtained | ||||
| Attended Services | Junior College | Bachelor | Graduate | Total |
| Yes | 62 | 146 | 76 | 284 |
| No | 101 | 232 | 105 | 438 |
Thus, combining the total obtained from the above table and the column of “High school”. The
| Highest Degree obtained | ||
| Attended Services | High School | Degrees beyond High School |
| Yes | 62 | 284 |
| No | 101 | 438 |
The claim is to test whether there is any relationship between getting a degree beyond high school and attended religious services.
The hypotheses used for testing are given below:
Software procedure:
Step by step procedure for calculating the chi-square test statistic using MINITAB software.
- Click on Stat, select Tables and then click on Chi-square Test (Two-way table in a worksheet).
- Under Columns containing the table: enter the columns of High School and Degree beyond high school.
- Click ok.
Output obtained from MINITAB is given below:
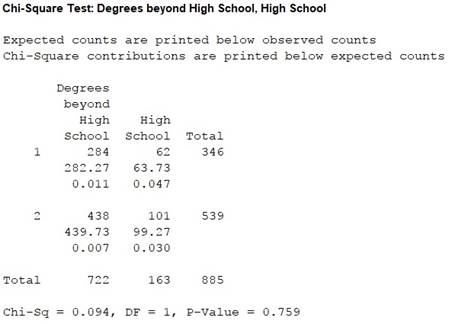
Thus, the test statistic is 0.094, the degree of freedom is 1 and the P-value is 0.759.
Since all the expected frequencies are greater than 5, the usage of chi-square test is appropriate.
Conclusion:
The P-value is 0.759 and level of significance is 0.05
Thus, the P-value is greater than the level of significance.
The null hypothesis is not rejected.
Thus, there is no sufficient evidence to support the claim that there is a relationship between getting a degree beyond high school and attended religious services.
d.
To explain: The relationship between the highest degree obtained and attending religious services in part (a), (b) and (c).
To find: The percentage who attended religious services across each category of highest degree obtained.
d.
Answer to Problem 25.44E
The relationship between the highest degree obtained and attending religious services depends on the individuals or the samples because High school people have higher percentage in attending religious service.
After omitting the “High School” column, the analysis shows no relationship between the highest degree obtained and attending religious services.
The percentage who attended religious services across each category of highest degree is given below:
| Highest Degree Hold | Percentage of Attended services |
| High School | 58.5% |
| Junior College | 9.1% |
| Bachelor | 21.3% |
| Graduate | 11.1% |
Explanation of Solution
From the analysis obtained in part (a), there is a relationship between the attended religious services and highest degree.
From the analysis obtained in part (b), there is no relationship between the attended religious services and highest degree because the column “High school” is left out from the analysis.
From the analysis obtained in part (c), there is no relationship between the attended religious services and highest degree because the columns of “Junior School”, “Bachelor” and “Graduate” and the analysis was carried out.
The above result shows that the highest degree is affected by attending religious services.
Calculation:
The percentage who attended religious services across each category of highest degree is calculated below:
| Highest Degree Hold | Percentage of Attended services |
| High School | |
| Junior College | |
| Bachelor | |
| Graduate |
Want to see more full solutions like this?
Chapter 25 Solutions
Basic Practice of Statistics (Instructor's)
- For a binary asymmetric channel with Py|X(0|1) = 0.1 and Py|X(1|0) = 0.2; PX(0) = 0.4 isthe probability of a bit of “0” being transmitted. X is the transmitted digit, and Y is the received digit.a. Find the values of Py(0) and Py(1).b. What is the probability that only 0s will be received for a sequence of 10 digits transmitted?c. What is the probability that 8 1s and 2 0s will be received for the same sequence of 10 digits?d. What is the probability that at least 5 0s will be received for the same sequence of 10 digits?arrow_forwardV2 360 Step down + I₁ = I2 10KVA 120V 10KVA 1₂ = 360-120 or 2nd Ratio's V₂ m 120 Ratio= 360 √2 H I2 I, + I2 120arrow_forwardQ2. [20 points] An amplitude X of a Gaussian signal x(t) has a mean value of 2 and an RMS value of √(10), i.e. square root of 10. Determine the PDF of x(t).arrow_forward
- In a network with 12 links, one of the links has failed. The failed link is randomlylocated. An electrical engineer tests the links one by one until the failed link is found.a. What is the probability that the engineer will find the failed link in the first test?b. What is the probability that the engineer will find the failed link in five tests?Note: You should assume that for Part b, the five tests are done consecutively.arrow_forwardProblem 3. Pricing a multi-stock option the Margrabe formula The purpose of this problem is to price a swap option in a 2-stock model, similarly as what we did in the example in the lectures. We consider a two-dimensional Brownian motion given by W₁ = (W(¹), W(2)) on a probability space (Q, F,P). Two stock prices are modeled by the following equations: dX = dY₁ = X₁ (rdt+ rdt+0₁dW!) (²)), Y₁ (rdt+dW+0zdW!"), with Xo xo and Yo =yo. This corresponds to the multi-stock model studied in class, but with notation (X+, Y₁) instead of (S(1), S(2)). Given the model above, the measure P is already the risk-neutral measure (Both stocks have rate of return r). We write σ = 0₁+0%. We consider a swap option, which gives you the right, at time T, to exchange one share of X for one share of Y. That is, the option has payoff F=(Yr-XT). (a) We first assume that r = 0 (for questions (a)-(f)). Write an explicit expression for the process Xt. Reminder before proceeding to question (b): Girsanov's theorem…arrow_forwardProblem 1. Multi-stock model We consider a 2-stock model similar to the one studied in class. Namely, we consider = S(1) S(2) = S(¹) exp (σ1B(1) + (M1 - 0/1 ) S(²) exp (02B(2) + (H₂- M2 where (B(¹) ) +20 and (B(2) ) +≥o are two Brownian motions, with t≥0 Cov (B(¹), B(2)) = p min{t, s}. " The purpose of this problem is to prove that there indeed exists a 2-dimensional Brownian motion (W+)+20 (W(1), W(2))+20 such that = S(1) S(2) = = S(¹) exp (011W(¹) + (μ₁ - 01/1) t) 롱) S(²) exp (021W (1) + 022W(2) + (112 - 03/01/12) t). where σ11, 21, 22 are constants to be determined (as functions of σ1, σ2, p). Hint: The constants will follow the formulas developed in the lectures. (a) To show existence of (Ŵ+), first write the expression for both W. (¹) and W (2) functions of (B(1), B(²)). as (b) Using the formulas obtained in (a), show that the process (WA) is actually a 2- dimensional standard Brownian motion (i.e. show that each component is normal, with mean 0, variance t, and that their…arrow_forward
- The scores of 8 students on the midterm exam and final exam were as follows. Student Midterm Final Anderson 98 89 Bailey 88 74 Cruz 87 97 DeSana 85 79 Erickson 85 94 Francis 83 71 Gray 74 98 Harris 70 91 Find the value of the (Spearman's) rank correlation coefficient test statistic that would be used to test the claim of no correlation between midterm score and final exam score. Round your answer to 3 places after the decimal point, if necessary. Test statistic: rs =arrow_forwardBusiness discussarrow_forwardBusiness discussarrow_forward
- I just need to know why this is wrong below: What is the test statistic W? W=5 (incorrect) and What is the p-value of this test? (p-value < 0.001-- incorrect) Use the Wilcoxon signed rank test to test the hypothesis that the median number of pages in the statistics books in the library from which the sample was taken is 400. A sample of 12 statistics books have the following numbers of pages pages 127 217 486 132 397 297 396 327 292 256 358 272 What is the sum of the negative ranks (W-)? 75 What is the sum of the positive ranks (W+)? 5What type of test is this? two tailedWhat is the test statistic W? 5 These are the critical values for a 1-tailed Wilcoxon Signed Rank test for n=12 Alpha Level 0.001 0.005 0.01 0.025 0.05 0.1 0.2 Critical Value 75 70 68 64 60 56 50 What is the p-value for this test? p-value < 0.001arrow_forwardons 12. A sociologist hypothesizes that the crime rate is higher in areas with higher poverty rate and lower median income. She col- lects data on the crime rate (crimes per 100,000 residents), the poverty rate (in %), and the median income (in $1,000s) from 41 New England cities. A portion of the regression results is shown in the following table. Standard Coefficients error t stat p-value Intercept -301.62 549.71 -0.55 0.5864 Poverty 53.16 14.22 3.74 0.0006 Income 4.95 8.26 0.60 0.5526 a. b. Are the signs as expected on the slope coefficients? Predict the crime rate in an area with a poverty rate of 20% and a median income of $50,000. 3. Using data from 50 workarrow_forward2. The owner of several used-car dealerships believes that the selling price of a used car can best be predicted using the car's age. He uses data on the recent selling price (in $) and age of 20 used sedans to estimate Price = Po + B₁Age + ε. A portion of the regression results is shown in the accompanying table. Standard Coefficients Intercept 21187.94 Error 733.42 t Stat p-value 28.89 1.56E-16 Age -1208.25 128.95 -9.37 2.41E-08 a. What is the estimate for B₁? Interpret this value. b. What is the sample regression equation? C. Predict the selling price of a 5-year-old sedan.arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





