
The upward velocity of a rocket can be computed by the following formula:
Where
To calculate: The height of the rocket at
Answer to Problem 46P
Solution:
All the results are summarized in the table below,
Acceleration graph is shown below.
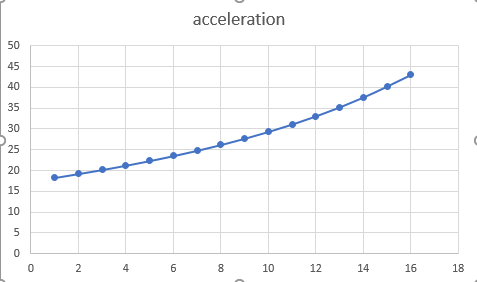
Explanation of Solution
Given Information:
The formula for the upward velocity of rocket is given as,
Here,
Formula Used:
6-segment Trapezoidal rule.
6-segmentSimpson’s 1/3 rule.
Change of variable formula.
Here,
Error Calculation.
Calculation:
Calculate the upward velocity of the rocket.
Substitute thegiven values in equation(1),
Apply 6-segment Trapezoidal rule for
Here,
Substitute
Expand the above terms.
Calculate
Substitute
Calculate
Substitute
Calculate
Substitute
Similarly, calculate all the function values.
Substitute above values in equation(3),
The formula for 6-segment Simpson’s 1/3 rule,
Substitute the function values from above,
The given velocity Integral is,
Change of variable before integrating the function,
And
Here,
Substitute the values of
Substitute the values of
Thus, the transformed function is,
Apply Six-Point Gauss Quadrature formula.
Calculate
Substitute
Calculate
Substitute
Similarly, calculate all function values.
Substitute the values in Six-Point Gauss Quadrature formula.
Apply Romberg Integration.
Choose
Substitute value from above and calculate
Choose
Substitute values from above and calculate
Choose
Substitute values from above and calculate
Choose
Substitute values from above and calculate
Substitute values from above and calculate
Calculate the approximate error,
Substitute values from above.
Substitute values from above and calculate
Substitute values from above and calculate
Substitute values from above and calculate
Calculate the approximate error,
Substitute values from above,
Substitute values from above and calculate
Substitute values from above and calculate
Calculate the approximate error as,
Substitute values from above.
All above calculated results are summarized in the table below,
UseNumerical differentiation to calculate acceleration as a function of time.
Apply finite-divided differences for
Apply centred differences to calculate the intermediate values,
Similarly, calculate all intermediate values of acceleration.
Apply backward difference for the last value at t = 30 s,
All of the results are displayed in the following table and graph,
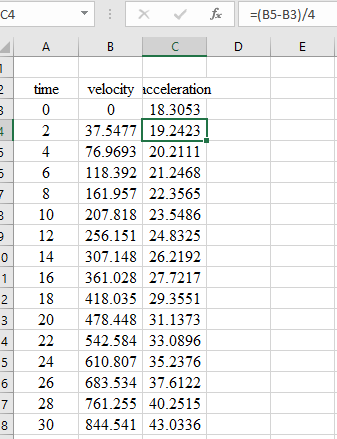
Select the time and acceleration column and go to insert chart and scattered chart. The graph of acceleration verses time is plotted as follows:

Want to see more full solutions like this?
Chapter 24 Solutions
Numerical Methods For Engineers, 7 Ed
- Find all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forward
- Let A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective. why?(b) Determine if f is surjective. why?(c) Based upon (a) and (b), is f bijective? why?arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective.(b) Determine if f is surjective. (c) Based upon (a) and (b), is f bijective?arrow_forward
- 1 S 0 sin(lnx) x² - 1 Inx dxarrow_forward2 6. Modelling. Suppose that we have two tanks (A and B) between which a mixture of brine flows. Tank A contains 200 liters of water in which 50 kilograms of salt has been dissolved and Tank B contains 100 liters of pure water. Water containing 1kg of salt per liter is pumped into Tank A at the rate of 5 liters per minute. Brine mixture is pumped into Tank A from Tank B at the rate of 3 liters per minute and brine mixture is pumped from Tank A into Tank B at the rate of 8 liters per minute. Brine is drained from Tank B at a rate of 5 liters per minute. (a) Draw and carefully label a picture of the situation, including both tanks and the flow of brine between them. JankA 1ks of Salt Slits Pump EL Brine mit tark A from tank 13 Tank 13 k 3L zooliters of Ico liters of water with pure water. Saky salt → 777 disslore inside Brine mix is pumped from tank A to B of 82 Brine drainen min by Gf salt (b) Assume all brine mixtures are well-stirred. If we let t be the time in minutes, let x(t) 1ks…arrow_forwardNo chatgpt plsarrow_forward
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal LittellAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal LittellAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



