
Each type of cost for all three jobs.
Answer to Problem 41A
Job 1:
Labor cost percentage is
Material cost percentage is
Overhead cost percentage is
Job 2:
Labor cost percentage is
Material cost percentage is
Overhead cost percentage is
Job 3:
Labor cost percentage is
Material cost percentage is
Overhead cost percentage is
Explanation of Solution
Given information:
Manufacturing cost consists of labor costs, material cost and overhead cost. Total manufacturing cost for job
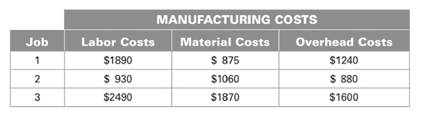
Calculation:
Components of manufacturing cost is given as below.
| Job | Labor Cost | Material cost | Overhead cost | Total cost |
Now we need to find the individual cost percentage for each job. Total cost will be base and individual costs will be percentage.
As we know the proportion to find percentage is given as
Job 1:
Labor cost
Putting these value in standard proportion,
Hence, the labor cost percentage is
Similarly,
Material cost
Putting these value in standard proportion,
Hence, the material cost percentage is
Again,
Overhead cost
Putting these value in standard proportion,
Hence, the Overhead cost percentage is
Job 2:
Labor cost
Putting these value in standard proportion,
Hence, the labor cost percentage is
Similarly,
Material cost
Putting these value in standard proportion,
Hence, the material cost percentage is
Again,
Overhead cost
Putting these value in standard proportion,
Hence, the Overhead cost percentage is
Job 3:
Labor cost
Putting these value in standard proportion,
Hence, the labor cost percentage is
Similarly,
Material cost
Putting these value in standard proportion,
Hence, the material cost percentage is
Again, Overhead cost
Putting these value in standard proportion,
Hence, the overhead cost percentage is
Thus,
Job 1:
Labor cost percentage is
Material cost percentage is
Overhead cost percentage is
Job 2:
Labor cost percentage is
Material cost percentage is
Overhead cost percentage is
Job 3:
Labor cost percentage is
Material cost percentage is
Overhead cost percentage is
Want to see more full solutions like this?
Chapter 24 Solutions
Mathematics For Machine Technology
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Complete solution requiredarrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Do on pen and paper onlyarrow_forwardProblem 9: The 30-kg pipe is supported at A by a system of five cords. Determine the force in each cord for equilibrium. B 60º A E Harrow_forwardd((x, y), (z, w)) = |xz|+|yw|, show that whether d is a metric on R² or not?. Q3/Let R be a set of real number and d: R² x R² → R such that -> d((x, y), (z, w)) = max{\x - zl, ly - w} show that whether d is a metric on R² or not?. Q4/Let X be a nonempty set and d₁, d₂: XXR are metrics on X let d3,d4, d5: XX → R such that d3(x, y) = 4d2(x, y) d4(x, y) = 3d₁(x, y) +2d2(x, y) d5(x,y) = 2d₁ (x,y))/ 1+ 2d₂(x, y). Show that whether d3, d4 and d5 are metric on X or not?arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning





