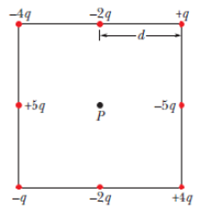
Chapter 24, Problem 1Q

Figure 24-24 shows eight particles that form a square, with distance d between adjacent particles. What is the net electric potential at point P at the center of the square if we take the electric potential to be zero at infinity?

Figure 24-24 Question 1.

To determine

To find:

the net electric potential at P, the center of a square array of charged  particles.

Answer to Problem 1Q

Solution:

The net electric potential at P is $k \frac{(-4q)}{d}$

Explanation of Solution

1) Concept

Electric potential obeys superposition principle. It means, the net potential at a point is the sum of potential contribution by each charge. Potential is written with the same sign as the charge contributing to it.

2) Formulae

i. Electric potential at a point due to a point charge q

$V= k \frac{q}{r}$

Where k- $\frac{1}{4\pi {\epsilon }_o} called$ Coulomb’s constant which is equal to 8.99 x 10^{9 $\frac{N.m^2}{C^2}$}

r- is the distance of the point from the charge

ii. Superposition of potential

Net electric potential= k Σ$( \frac{q_1}{r_1}+ \frac{q_2}{r_2}+\dots \frac{q_n}{r_n})$

3) Given

i. Fig. 24.24 showing 8 particles that form a square.

ii. Distance between two adjacent charges= d

iii. Charges at the top face from left to right: -4q, -2q, +q

iv. Charges at the bottom face from left to right: -q_, -2q_, +4q

v. Charge at the middle of left side=+5q

vi. Charge at the middle of right side=-5q

vii. Potential (V) is zero at infinity

4) Calculations

Corner particles are equidistant from the center.

Total charge of corner particles= -4q+q-q+4q=0

Therefore, the net potential at the center due to the corner particles is zero. Hence, the net potential is contributed only by the particles located in the middle of faces.

Using the formula and superposition of electric potential, the net potential

V= $k \frac{(-2q)}{d}$+ $k \frac{(-5q)}{d}$+ $k \frac{(-2q)}{d}$+ $k \frac{(+5q)}{d}$+

= $k \frac{(-4q)}{d}$

The net electric potential at the center is $k \frac{(-4q)}{d}$

Conclusion:

Using the superposition of electric potential, net electric potential at the given point is determined.