Linear Algebra: A Modern Introduction
4th Edition
ISBN: 9781285463247
Author: David Poole
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2.4, Problem 19EQ
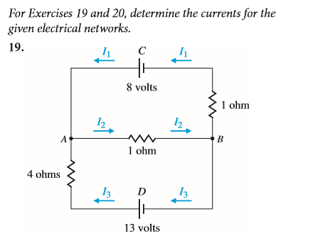
For Exercises 19 and 20, determine the currents for the given electrical networks.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
10-2
Let A =
02-4
and b =
4
Denote the columns of A by a₁, a2, a3, and let W = Span {a1, a2, a̸3}.
-4 6
5
- 35
a. Is b in {a1, a2, a3}? How many vectors are in {a₁, a₂, a3}?
b. Is b in W? How many vectors are in W?
c. Show that a2 is in W. [Hint: Row operations are unnecessary.]
a. Is b in {a₁, a2, a3}? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your
choice.
○ A. No, b is not in {a₁, a2, 3} since it cannot be generated by a linear combination of a₁, a2, and a3.
B. No, b is not in (a1, a2, a3}
since b is not equal to a₁, a2, or a3.
C. Yes, b is in (a1, a2, a3} since b = a
(Type a whole number.)
D. Yes, b is in (a1, a2, 3} since, although b is not equal to a₁, a2, or a3, it can be expressed as a linear
combination of them. In particular, b =
+
+
☐ az.
(Simplify your answers.)
14
14
4. The graph shows the printing rate of Printer A. Printer B can
print at a rate of 25 pages per minute. How does the printing
rate for Printer B compare to the printing rate for Printer A?
The printing rate for Printer B is
than the rate
for Printer A because the rate of 25 pages per minute
is
than the rate of
for Printer A.
pages per minute
RIJOUT
40
fy
Printer Rat
Number of Pages
8N WA
10
30
20
Printer A
0
0
246
Time (min)
X
OR
16 f(x) =
Ef 16
χ
по
x²-2 410 | y = (x+2) + 4
Y-INT: y = 0
X-INT: X=0
VA: x=2
OA: y=x+2
0
X-INT: X=-2
X-INT: y = 2
VA
0
2
whole.
2-2
4
y - (x+2) = 27-270
+
xxx> 2
क्
above OA
(x+2) OA
x-2/x²+0x+0
2
x-2x
2x+O
2x-4
4
X<-1000 4/4/2<0 below Of
y
VA
X=2
X-2
OA
y=x+2
-2
2
(0,0)
2
χ
Chapter 2 Solutions
Linear Algebra: A Modern Introduction
Ch. 2.1 - In Exercises 1-6, determine which equations are...Ch. 2.1 - In Exercises 1-6, determine which equations are...Ch. 2.1 - In Exercises 1-6, determine which equations are...Ch. 2.1 - In Exercises 1-6, determine which equations are...Ch. 2.1 - In Exercises 1-6, determine which equations are...Ch. 2.1 - In Exercises 1-6, determine which equations are...Ch. 2.1 - In Exercises 7-10, find a linear equation that has...Ch. 2.1 - In Exercises 7-10, find a linear equation that has...Ch. 2.1 - In Exercises 7-10, find a linear equation that has...Ch. 2.1 - In Exercises 7-10, find a linear equation that has...
Ch. 2.1 - Prob. 11EQCh. 2.1 - In Exercises 11-14, find the solution set of each...Ch. 2.1 - In Exercises 11-14, find the solution set of each...Ch. 2.1 - In Exercises 11-14, find the solution set of each...Ch. 2.1 - In Exercises 19-24, solve the given system by back...Ch. 2.1 - In Exercises 19-24, solve the given system by back...Ch. 2.1 - In Exercises 19-24, solve the given system by back...Ch. 2.1 - In Exercises 19-24, solve the given system by back...Ch. 2.1 - In Exercises 19-24, solve the given system by back...Ch. 2.1 - In Exercises 19-24, solve the given system by back...Ch. 2.1 - The systems in Exercises 25 and 26 exhibit a lower...Ch. 2.1 - The systems in Exercises 25 and 26 exhibit a lower...Ch. 2.1 - Find the augmented matrices of the linear systems...Ch. 2.1 - Find the augmented matrices of the linear systems...Ch. 2.1 - Find the augmented matrices of the linear systems...Ch. 2.1 - Prob. 30EQCh. 2.1 - In Exercises 31 and 32, find a system of linear...Ch. 2.1 - Prob. 32EQCh. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 1-8, determine whether the given...Ch. 2.2 - In Exercises 9-14, use elementary row operations...Ch. 2.2 - In Exercises 9-14, use elementary row operations...Ch. 2.2 - In Exercises 9-14, use elementary row operations...Ch. 2.2 - In Exercises 9-14, use elementary row operations...Ch. 2.2 - In Exercises 9-14, use elementary row operations...Ch. 2.2 - In Exercises 9-14, use elementary row operations...Ch. 2.2 - 15. Reverse the elementary row operations used in...Ch. 2.2 - 16. In general, what is the elementary row...Ch. 2.2 - Prob. 17EQCh. 2.2 - In Exercises 17 and 18, show that the given...Ch. 2.2 - 19. What is wrong with the following “proof” that...Ch. 2.2 - What is the net effect of performing the following...Ch. 2.2 - Students frequently perform the following type of...Ch. 2.2 - Consider the matrix A=[2314]. Show that any of the...Ch. 2.2 - What is the rank of each of the matrices in...Ch. 2.2 - Prob. 24EQCh. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.2 - In Exercises 25-34, solve the given system of...Ch. 2.3 - In Exercises 1-6, determine if the vector is a...Ch. 2.3 - In Exercises 1-6, determine if the vector is a...Ch. 2.3 - In Exercises 1-6, determine if the vector is a...Ch. 2.3 - In Exercises 1-6, determine if the vector vis a...Ch. 2.3 - In Exercises 1-6, determine if the vector is a...Ch. 2.3 - In Exercises 7 and 8, determine if the vector b is...Ch. 2.3 - Show that 3=span([101],[110],[011])Ch. 2.3 - Use the method of Example 2.23 and Theorem 2.6 to...Ch. 2.3 - Use the method of Example 2.23 and Theorem 2.6 to...Ch. 2.3 - Use the method of Example 2.23 and Theorem 2.6 to...Ch. 2.4 - 1. Suppose that, in Example 2.27, 400 units of...Ch. 2.4 - 2. Suppose that in Example 2.27, 400 units of food...Ch. 2.4 - A florist offers three sizes of flower...Ch. 2.4 - 4. (a) In your pocket you have some nickels,...Ch. 2.4 - 5. A coffee merchant sells three blends of coffee....Ch. 2.4 - Redo Exercise 5, assuming that the house blend...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - In Exercises 7-14, balance the chemical equation...Ch. 2.4 - For Exercises 19 and 20, determine the currents...Ch. 2.4 - For Exercises 19 and 20, determine the currents...Ch. 2.4 - 21. (a) Find the currents in the bridge circuit...Ch. 2.4 -
22. The networks in parts (a) and (b) of Figure...Ch. 2.4 -
23. Consider a simple economy with just two...Ch. 2.4 - Suppose the coal and steel industries form a...Ch. 2.4 -
25. A painter, a plumber, and an electrician...Ch. 2.4 -
31. In Example 2.35, describe all possible...Ch. 2 - What is the maximum rank of a 53 matrix? What is...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- I need help solving the equation 3x+5=8arrow_forwardWhat is the domain, range, increasing intervals (theres 3), decreasing intervals, roots, y-intercepts, end behavior (approaches four times), leading coffiencent status (is it negative, positivie?) the degress status (zero, undifined etc ), the absolute max, is there a absolute minimum, relative minimum, relative maximum, the root is that has a multiplicity of 2, the multiplicity of 3.arrow_forwardWhat is the vertex, axis of symmerty, all of the solutions, all of the end behaviors, the increasing interval, the decreasing interval, describe all of the transformations that have occurred EXAMPLE Vertical shrink/compression (wider). or Vertical translation down, the domain and range of this graph EXAMPLE Domain: x ≤ -1 Range: y ≥ -4.arrow_forward
- 4. Select all of the solutions for x²+x - 12 = 0? A. -12 B. -4 C. -3 D. 3 E 4 F 12 4 of 10arrow_forward2. Select all of the polynomials with the degree of 7. A. h(x) = (4x + 2)³(x − 7)(3x + 1)4 B h(x) = (x + 7)³(2x + 1)^(6x − 5)² ☐ Ch(x)=(3x² + 9)(x + 4)(8x + 2)ª h(x) = (x + 6)²(9x + 2) (x − 3) h(x)=(-x-7)² (x + 8)²(7x + 4)³ Scroll down to see more 2 of 10arrow_forward1. If all of the zeros for a polynomial are included in the graph, which polynomial could the graph represent? 100 -6 -2 0 2 100 200arrow_forward
- 3. Select the polynomial that matches the description given: Zero at 4 with multiplicity 3 Zero at −1 with multiplicity 2 Zero at -10 with multiplicity 1 Zero at 5 with multiplicity 5 ○ A. P(x) = (x − 4)³(x + 1)²(x + 10)(x — 5)³ B - P(x) = (x + 4)³(x − 1)²(x − 10)(x + 5)³ ○ ° P(x) = (1 − 3)'(x + 2)(x + 1)"'" (x — 5)³ 51 P(r) = (x-4)³(x − 1)(x + 10)(x − 5 3 of 10arrow_forwardMatch the equation, graph, and description of transformation. Horizontal translation 1 unit right; vertical translation 1 unit up; vertical shrink of 1/2; reflection across the x axis Horizontal translation 1 unit left; vertical translation 1 unit down; vertical stretch of 2 Horizontal translation 2 units right; reflection across the x-axis Vertical translation 1 unit up; vertical stretch of 2; reflection across the x-axis Reflection across the x - axis; vertical translation 2 units down Horizontal translation 2 units left Horizontal translation 2 units right Vertical translation 1 unit down; vertical shrink of 1/2; reflection across the x-axis Vertical translation 2 units down Horizontal translation 1 unit left; vertical translation 2 units up; vertical stretch of 2; reflection across the x - axis f(x) = - =-½ ½ (x − 1)²+1 f(x) = x²-2 f(x) = -2(x+1)²+2 f(x)=2(x+1)²-1 f(x)=-(x-2)² f(x)=(x-2)² f(x) = f(x) = -2x²+1 f(x) = -x²-2 f(x) = (x+2)²arrow_forwardWhat is the vertex, increasing interval, decreasing interval, domain, range, root/solution/zero, and the end behavior?arrow_forward
- The augmented matrix of a linear system has been reduced by row operations to the form shown. Continue the appropriate row operations and describe the solution set of the original system. 1 -1 0 1 -2 00-4 0-6 0 0 1 - 3 3 0 001 4arrow_forwardSolve the system. X1 - 3x3 = 10 4x1 + 2x2 + 3x3 = 22 ×2 + 4x3 = -2arrow_forwardUse the quadratic formula to find the zeros of the quadratic equation. Y=3x^2+48x+180arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY