Chapter 2.3, Problem 75E

C Problems 75 and 76 refer to the greatest integer function, which is denoted by 〚x〛 and is defined as

$〚x〛=greatestinteger\le x$

For example,

$\begin{array}{lll}〚-3.6〛\hfill & =\hfill & greatestinteger\le -3.6=-4\hfill \\ 〚2〛\hfill & =\hfill & greatestinteger\le 2=2\hfill \\ 〚2.5〛\hfill & =\hfill & greatestinteger\le 2.5=2\hfill \end{array}$

The graph of f(x) = 〚x〛 is shown. There, we can see that

$\begin{array}{lll}〚x〛=-2\hfill & for\hfill & -2\le x<-1\hfill \\ 〚x〛=-1\hfill & for\hfill & -1\le x<0\hfill \\ 〚x〛=0\hfill & for\hfill & 0\le x<1\hfill \\ 〚x〛=1\hfill & for\hfill & 1\le x<2\hfill \\ 〚x〛=2\hfill & for\hfill & 2\le x<3\hfill \end{array}$

and so on.

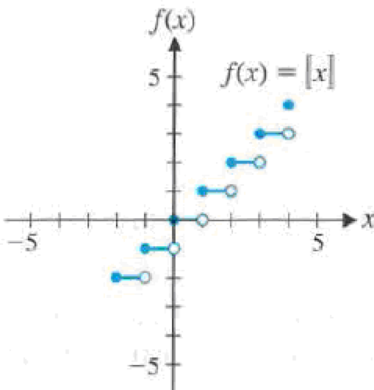
Figure for 75 and 76

75.

1. (A)   Is f continuous from the right at x = 0?
2. (B)   Is f continuous from the left at x = 0?
3. (C)   Is f continuous on the open interval (0, 1)?
4. (D)   Is f continuous on the closed interval [0, 1]?
5. (E)    Is f continuous on the half-closed interval [0, 1)?