
Concept explainers
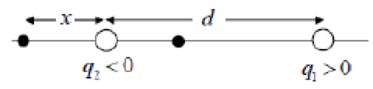
(a) Because of the inverse square nature of the electric field, any location where the field is zero must be closer to the weaker charge (q2). Also, in between the two charges, the fields due to the two charges are parallel to each other (both to the left) and cannot cancel. Thus the only places where the field can be zero are closer to the weaker charge, but not between them. In the diagram, this is the point to the left of q2. Take rightward as the positive direction.
(b) The potential due to the positive charge is positive everywhere, and the potential due to the negative charge is negative everywhere. Since the negative charge is smaller in magnitude than the positive charge, any point where the potential is zero must be closer to the negative charge. So consider locations between the charges (position x1) and to the left of the negative charge (position x2) as shown in the diagram.
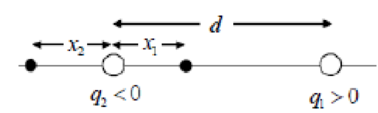
(II) Two point charges, 3.4 μC and −2.0μC, are placed 5.0 cm apart on the x axis. At what points along the x axis is (a) the electric field zero and (b) the potential zero? Let V = 0 at r = ∞.
Want to see the full answer?
Check out a sample textbook solution
Chapter 23 Solutions
Physics for Scientists and Engineers with Modern Physics
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
Campbell Essential Biology with Physiology (5th Edition)
Anatomy & Physiology (6th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Campbell Biology in Focus (2nd Edition)
- Part 2 - Geometry and Trigonometry 1. Line B touches the circle at a single point. Line A extends radially through the center of the circle. A B (a) Which line is tangential to the circumference of the circle? (b) What is the angle between lines A and B. 2. In the figure below what is the angle C? 30 45 3. In the figure below what is the value of the angle 0? 30° 4. In the figure below what is the value of the angle 0? A 30°arrow_forwardDetails solution No chatgpt plsarrow_forwardPlease solve and answer the problem correctly please.Thank you!!arrow_forward
- Will you please walk me through the calculations in more detail for solving this problem? I am a bit rusty on calculus and confused about the specific steps of the derivation: https://www.bartleby.com/solution-answer/chapter-3-problem-15e-modern-physics-2nd-edition/9780805303087/7cf8c31d-9476-46d5-a5a9-b897b16fe6fcarrow_forwardplease help with the abstract. Abstract - This document outlines the format of the lab report and describes the Excel assignment. The abstract should be a short paragraph that very briefly includes the experiment objective, method, result and conclusion. After skimming the abstract, the reader should be able to decide whether they want to keep reading your work. Both the format of the report and the error analysis are to be followed. Note that abstract is not just the introduction and conclusion combined, but rather the whole experiment in short including the results. I have attacted the theory.arrow_forwardUsing the Experimental Acceleration due to Gravity values from each data table, Data Tables 1, 2, and 3; determine the Standard Deviation, σ, mean, μ, variance, σ2 and the 95% Margin of Error (Confidence Level) Data: Ex. Acc. 1: 12.29 m/s^2. Ex. Acc. 2: 10.86 m/s^2, Ex. Acc. 3: 9.05 m/s^2arrow_forward
- In the Super Smash Bros. games the character Yoshi’s has a “ground pound” down special move where he launches himself downward to attack an enemy beneath him. A) If Yoshi flings himself downwards at 9.76 miles per hour to hit an enemy 10.5 m below him, how fast is Yoshi traveling when he hits the enemy? 1 mile = 1609 m B) How much time does it take Yoshi to hit the enemy beneath him?arrow_forwardNo chatgpt pls will upvotearrow_forwardSolve No chatgpt pls will upvotearrow_forward
- Can someone help me solve this thank you.arrow_forwardNo chatgpt pls will upvotearrow_forward1.62 On a training flight, a Figure P1.62 student pilot flies from Lincoln, Nebraska, to Clarinda, Iowa, next to St. Joseph, Missouri, and then to Manhattan, Kansas (Fig. P1.62). The directions are shown relative to north: 0° is north, 90° is east, 180° is south, and 270° is west. Use the method of components to find (a) the distance she has to fly from Manhattan to get back to Lincoln, and (b) the direction (relative to north) she must fly to get there. Illustrate your solutions with a vector diagram. IOWA 147 km Lincoln 85° Clarinda 106 km 167° St. Joseph NEBRASKA Manhattan 166 km 235° S KANSAS MISSOURIarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





