Chapter 2.3, Problem 24E

Solution

To Sketch: The given function with local and minimum extrema and $x-$ intercepts. And explain its end behaviour with upper and lower limits.

Given: $f\left(x\right)=-3x^4-5x^3+15x^2-5x+19$

Graph:

Sketch the graph of $f\left(x\right)=-3x^4-5x^3+15x^2-5x+19$with all its extrema and zeros.

  

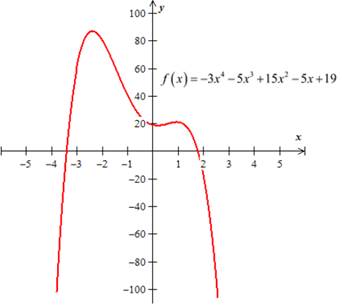
Find the extrema:

Find the first derivative of the function:

  $f\left(x\right)=-12x^3-15x^2+30x-5$

Find the second derivative of the function:

  $f^{\prime \prime }\left(x\right)=-36x^2-30x+30$

To find the local maximum and minimum values of the function, set the derivative equal to  $0$  and solve.

  $-12x^3-15x^2+30x-5=0$

Graph each side of the equation. The solution is the $x-$ value of the point of intersection.

  $x\approx -2.37599685,0.18669769,0.93929915$

Evaluate the second derivative at $x=-2.37599685$ . If the second derivative is positive, then this is a local minimum. If it is negative, then this is a local maximum.

  $\begin{array}{l}x=-36{(}^{-}-30\cdot -2.37599685+30\\ x=-101.95309251\end{array}$

  $x=-2.37599685$ is a local maximum because the value of the second derivative is positive.

Evaluate the second derivative at $x=0.18669769$ . If the second derivative is positive, then this is a local minimum. If it is negative, then this is a local maximum.

  $\begin{array}{c}x=-36{(}^{0.18669769}-30\cdot 0.18669769+30\\ =23.14425195\end{array}$

  $x=0.18669769$ is a local minimum because the value of the second derivative is negative.

Evaluate the second derivative at $x=0.93929915$ . If the second derivative is positive, then this is a local minimum. If it is negative, then this is a local maximum.

  $\begin{array}{l}x=-36{\left(0.93929915\right)}^2-30\cdot 0.93929915+30\\ x=-29.94115944\end{array}$

  $x=0.93929915$ is a local minimum because the value of the second derivative is positive.

Find the values of $y:$

Substitute $x=-2.37599685$ in $f\left(x\right)=-3x^4-5x^3+15x^2-5x+19$ : $\begin{array}{l}y=f\left(-2.37599685\right)=-3{\left(-2.37599685\right)}^4-5{\left(-2.37599685\right)}^3+15{\left(-2.37599685\right)}^2-5\times -2.37599685+19\\ y=87.01689633\end{array}$

Substitute $x=0.18669769$ in $f\left(x\right)=-3x^4-5x^3+15x^2-5x+19$:

  $\begin{array}{l}y=-3{\left(0.18669769\right)}^4-5{\left(0.18669769\right)}^3+15{\left(0.18669769\right)}^2-5\cdot 0.18669769+19\\ y=18.55316943\end{array}$

Substitute $x=0.93929915$ in $f\left(x\right)=-3x^4-5x^3+15x^2-5x+19$:

  $\begin{array}{l}y=-3{\left(0.93929915\right)}^4-5{\left(0.93929915\right)}^3+15{\left(0.93929915\right)}^2-5\cdot 0.93929915+19\\ y=21.05884047\end{array}$

The function $f$ has 3 extrema of about $21.058$ at $x\approx 0.939$ and of about $87.016$ at $x\approx -2.375$ and of about $18.553$ at $x\approx 0.186$ . The function has zeros at

Find the zeroes of the function $f\left(x\right)=2x^4-5x^3-17x^2+14x+41$:

  $2x^4-5x^3-17x^2+14x+41=0$

Graph each side of the equation. The solution is the x-value of the point of intersection. The function has zeros at $x\approx -3.4257487\left(\text{twice}\right),1.76957417\left(\text{twice}\right)$

Thus, the function $f$ has $3$ extrema and $4$ zeros, the maximum number possible for a quadratic.

End behaviour:

Use the limits to describe its end behaviour.

  $\underset{x\to \infty }{\lim }f\left(x\right)=\infty \text{ and }\underset{x\to -\infty }{\lim }f\left(x\right)=-\infty$

The graph falls to the left and falls to the right.