Chapter 2, Problem 92RE

Solution

(a)

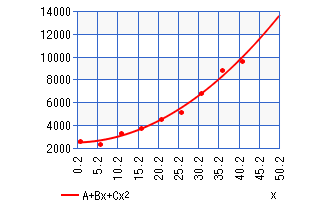
To find: The linear regression model and scatter graph.

The model of the given data $y=2479.1835+6.963x+4.277x^2$

Given information

The table for the given data is below.

period	1	6	11	16	21	26	31	36	41
temperature	2600	2390	3310	3720	4560	5110	6860	8820	9650

The equation is $y=ax+b{x}^2$ and the normal equations are

  ${\displaystyle \sum y=an+b{\displaystyle \sum x+c{\displaystyle \sum x^2}}}$

  ${\displaystyle \sum xy=a{\displaystyle \sum x}+b{\displaystyle \sum x^2+c{\displaystyle \sum x^3}}}$

  ${\displaystyle \sum x^{2}y=a{\displaystyle \sum x^2}+b{\displaystyle \sum x^3+c{\displaystyle \sum x^4}}}$

The values are calculated using the following table

x	y	x2	x3	x4	x·y	x2·y
1	2600	1	1	1	2600	2600
6	2390	36	216	1296	14340	86040
11	3310	121	1331	14641	36410	400510
16	3720	256	4096	65536	59520	952320
21	4560	441	9261	194481	95760	2010960
26	5110	676	17576	456976	132860	3454360
31	6860	961	29791	923521	212660	6592460
36	8820	1296	46656	1679616	317520	11430720
41	9650	1681	68921	2825761	395650	16221650
---	---	---	---	---	---	---
∑x=189	∑y=47020	${\displaystyle \sum x^2}$ =5469	${\displaystyle \sum x^3}$ =177849	${\displaystyle \sum x^4}$ =6161829	∑x·y=1267320	${\displaystyle \sum x^2}y$ =41151620

Substituting these values in the normal equations

9a+189b+5469c=47020

189a+5469b+177849c=1267320

5469a+177849b+6161829c=41151620

Solving these 3 equations,

Total Equations are 3

9a+189b+5469c=47020→(1)

189a+5469b+177849c=1267320→(2)

5469a+177849b+6161829c=41151620→(3)

Select the equations (1) and (2), and eliminate the variable a.

  

Select the equations (1) and (3), and eliminate the variable a.

  

Select the equations (4) and (5), and eliminate the variable b.

  

Now use back substitution method

From (6)

577500c=2470000

⇒c=2470000577500=4.2771

From (4)

-1500b-63000c=-279900

⇒-1500b-63000(4.2771)=-279900

⇒-1500b-269454.5455=-279900

⇒-1500b=-279900+269454.5455=-10445.4545

⇒b=-10445.4545-1500=6.9636

From (1)

9a+189b+5469c=47020

⇒9a+189(6.9636)+5469(4.2771)=47020

⇒9a+24707.3481=47020

⇒9a=47020-24707.3481=22312.6519

⇒a=22312.65199=2479.1835

Solution using Elimination method.

a=2479.1835,b=6.9636,c=4.2771

Now substituting this values in the equation is $y=ax+b{x}^2$ we get

  $y=2479.1835+6.963x+4.277x^2$

Scatter graph of the following data given below

  

(b)

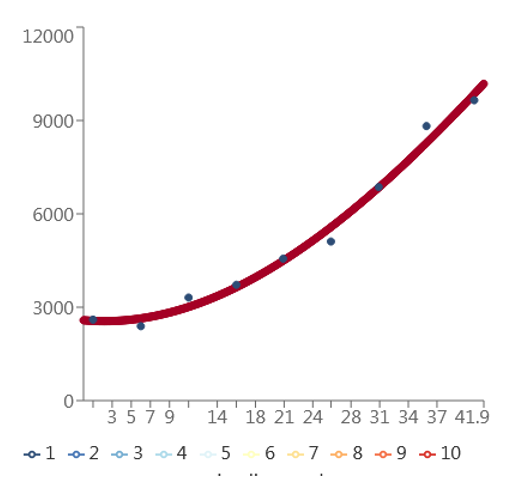
To find: The quadratic regression model and scatter graph.

The model of the given data $y=2581.7965-27.4415x+6.3855x^2-0.0335x^3$

Given information

The table for the given data is below.

period	1	6	11	16	21	26	31	36	41
temperature	2600	2390	3310	3720	4560	5110	6860	8820	9650

The equation is $y=a+bx+c{x}^2+d{x}^3$

  $\begin{array}{l}{\displaystyle \sum y=an+b{\displaystyle \sum x+c{\displaystyle \sum x^2+d{\displaystyle \sum x^3}}}}\\ {\displaystyle \sum xy=a{\displaystyle \sum x}+b{\displaystyle \sum x^2+c{\displaystyle \sum x^3+d{\displaystyle \sum x^4}}}}\\ {\displaystyle \sum x^2}y=a{\displaystyle \sum x^2}+b{\displaystyle \sum x^3}+c{\displaystyle \sum x^4}+d{\displaystyle \sum x^5}\\ {\displaystyle \sum x^{3}y=a{\displaystyle \sum x^3+b{\displaystyle \sum x^4+c{\displaystyle \sum x^5}}}}+d{\displaystyle \sum x^6}\end{array}$

The values are calculated using the following table

x	y	x2	x3	x4	x5	x6	x·y	x2·y	x3·y
1	2600	1	1	1	1	1	2600	2600	2600
6	2390	36	216	1296	7776	46656	14340	86040	516240
11	3310	121	1331	14641	161051	1771561	36410	400510	4405610
16	3720	256	4096	65536	1048576	16777216	59520	952320	15237120
21	4560	441	9261	194481	4084101	85766121	95760	2010960	42230160
26	5110	676	17576	456976	11881376	308915776	132860	3454360	89813360
31	6860	961	29791	923521	28629151	887503681	212660	6592460	204366260
36	8820	1296	46656	1679616	60466176	2176782336	317520	11430720	411505920
41	9650	1681	68921	2825761	115856201	4750104241	395650	16221650	665087650
---	---	---	---	---	---	---	---	---	---
∑x=189	∑y=47020	∑x2=5469	∑x3=177849	∑x4=6161829	∑x5=222134409	∑x6=8227667589	∑x·y=1267320	∑x2·y=41151620	∑x3·y=1433164920

Substituting these values in the normal equations

9a+189b+5469c+177849d=47020

189a+5469b+177849c+6161829d=1267320

5469a+177849b+6161829c+222134409d=41151620

177849a+6161829b+222134409c+8227667589d=1433164920

Solving these 4 equations,

Total Equations are 4

9a+189b+5469c+177849d=47020→(1)

189a+5469b+177849c+6161829d=1267320→(2)

5469a+177849b+6161829c+222134409d=41151620→(3)

177849a+6161829b+222134409c+8227667589d=1433164920→(4)

Select the equations (1) and (2), and eliminate the variable a.

  

Select the equations (1) and (3), and eliminate the variable a.

  

Select the equations (1) and (4), and eliminate the variable a.

  

Select the equations (5) and (6), and eliminate the variable b.

  

Select the equations (5) and (7), and eliminate the variable b.

  

Select the equations (8) and (9), and eliminate the variable c.

  

Now use back substitution method

From (10)

-22275000d=745500

⇒d=745500-22275000=-0.0335

From (8)

577500c+36382500d=2470000

⇒577500c+36382500(-0.0335)=2470000

⇒577500c-1217650=2470000

⇒577500c=2470000+1217650=3687650

⇒c=3687650577500=6.3855

From (5)

-1500b-63000c-2427000d=-279900

⇒-1500b-63000(6.3855)-2427000(-0.0335)=-279900

⇒-1500b-321062.2222=-279900

⇒-1500b=-279900+321062.2222=41162.2222

⇒b=41162.2222-1500=-27.4415

From (1)

9a+189b+5469c+177849d=47020

⇒9a+189(-27.4415)+5469(6.3855)+177849(-0.0335)=47020

⇒9a+23783.8317=47020

⇒9a=47020-23783.8317=23236.1683

⇒a=23236.16839=2581.7965

Solution using Elimination method.

a=2581.7965,b=-27.4415,c=6.3855,d=-0.0335

Now substituting this values in the equation is $y=a+bx+c{x}^2+d{x}^3$ , we get

  $y=2581.7965-27.4415x+6.3855x^2-0.0335x^3$

Scatter graph of the model is given below.

  

(c)

To find: The cost of tuition fee in 2021.

According to quadratic regression the cost of tuition fee in 2021 is 11849 .

According to cubic regression the cost of tuition fee in 2021 is 14082

Given informationquadratic regression is $y=2479.1835+6.963x+4.277x^2$

Substitute x=46 in the above equation

  $\begin{array}{l}y=2479.1835+6.963\left(46\right)+4.277{\left(46\right)}^2\\ y=11849\end{array}$

Cubic equation model is $y=2581.7965-27.4415x+6.3855x^2-0.0335x^3$

Now Substitute x=46 in the above equation

  $\begin{array}{l}y=2581.7965-27.4415\left(46\right)+6.3855{\left(46\right)}^2-0.0335{\left(46\right)}^3\\ y=14082\end{array}$

(d)

To find: The end behaviour of the model.

The model of the given data $y=2479.1835+6.963x+4.277x^2$

Given information

According to quadratic model the future expense will not go too high. But the cubic model says otherwise. It predicts that future expanse will be very high.