Chapter 23, Problem 23.18P

Particle A of charge 3.00 × 10⁻⁴ C is at the origin, particle B of charge −6.00 × 10⁻⁴ C is at (4.00 m, 0), and particle C of charge 1.00 × 10⁻⁴ C is at (0, 3.00 m). We wish to find the net electric force on C. (a) What is the x component of the electric force exerted by A on C? (b) What is the y component of the force exerted by A on C? (c) Find the magnitude of the force exerted by B on C. (d) Calculate the x component of the force exerted by B on C. (e) Calculate the y component of the force exerted by B on C. (f) Sum the two x components from parts (a) and (d) to obtain the resultant x component of the electric force acting on C. (g) Similarly, find the y component of the resultant force vector acting on C. (h) Find the magnitude and direction of the resultant electric force acting on C.

To determine

The $x-$ component of the electric force exerted by $A$ on $C$.

Answer to Problem 23.18P

The $x-$ component of the electric force exerted by $A$ on $C$ is $0$.

Explanation of Solution

The charge of particle $A$ is $3.00\times {10}^{-4}\text{C}$, charge of particle $B$ is $-6.00\times {10}^{-4}\text{C}$, and charge of particle $C$ is $1.00\times {10}^{-4}\text{C}$, location of particle $A$ is origin, location of particle $B$ is $\left(4.00\text{m,}\text{0}\right)$ and  location of particle $C$ is $\left(0,3.00\text{m}\right)$.

The diagram for the given condition is shown below.

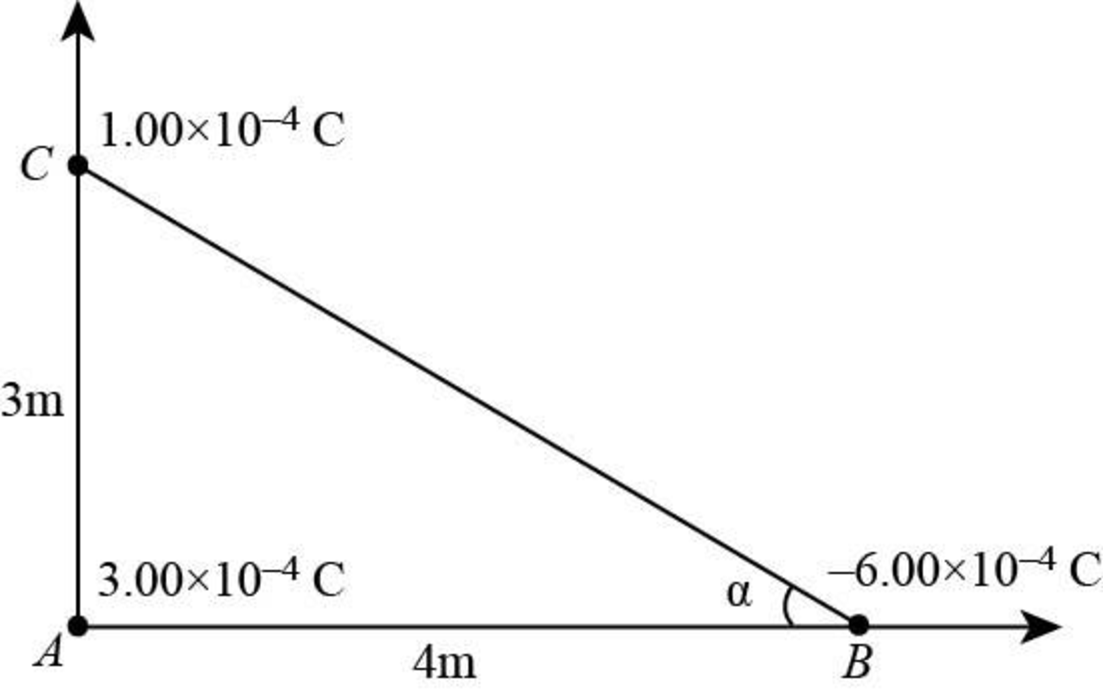
Figure 1

Write the formula to calculate the electrical force

    $F_{{\text{AC}}_{\text{x}}}=\frac{k_e{q}_1{q}_2}{r^2}$

Here, $k_e$ is the constant, $q_1$ is the charge on particle $A$, $q_2$ is the charge on particle $C$ and $r$ is the distance between the particles $A$ and $C$ on $x-$ axis.

The particle $A$ is at origin that is the abscissa and the ordinate both are $0$ and the particle $C$ is at the distance of $3.00\text{m}$ from the $y-$ axis and the abscissa is $0$.

The distance from the $x-$ axis is $0$ for both the particles $A$ and $C$. So, no net force will act on the particle $A$ by $C$ in the x-direction

Thus, the $x$ component of the electric force exerted by $A$ on $C$

    $F_{{\text{AC}}_{\text{x}}}=0$

Conclusion:

Therefore, the $x$ component of the electric force exerted by $A$ on $C$ is $0$.

To determine

The $y-$ component of the force exerted by $A$ on $C$.

Answer to Problem 23.18P

The $y-$ component of the force exerted by $A$ on $C$ is $30\text{N}$.

Explanation of Solution

Write the formula to calculate the electrical force

    $F_{{\text{AC}}_{\text{y}}}=\frac{k_e{q}_1{q}_2}{r^2}$

Substitute $3.00\times {10}^{-4}\text{C}$ for $q_1$, $1.00\times {10}^{-4}\text{C}$ for $q_2$, $3.00\text{m}$ to calculate $F_{{\text{AC}}_{\text{y}}}$ as,

    $\begin{array}{c}{F}_{{\text{AC}}_{\text{y}}}=\frac{\left(9\times {10}^9\text{N}\cdot {\text{m}}^2/{\text{C}}^2\right)\left(3.00\times {10}^{-4}\text{C}\right)\left(1.00\times {10}^{-4}\text{C}\right)}{{\left(3.00\text{m}\right)}^2}\\ =30.0\text{N}\end{array}$

Conclusion:

Therefore, the $y-$ component of the force exerted by $A$ on $C$ is $30\text{N}$.

To determine

The magnitude of the force exerted by $B$ on $C$.

Answer to Problem 23.18P

The magnitude of the force exerted by $B$ on $C$ is $21.6\text{N}$.

Explanation of Solution

By Pythagoras theorem, write the expression distance between $B$ and $C$

    $\begin{array}{c}{\left(BC\right)}^2={\left(AC\right)}^2+{\left(AB\right)}^2\\ ={\left(3\text{m}\right)}^2+{\left(4\text{m}\right)}^2\\ BC=\sqrt{\left(16+9\right){\text{m}}^{\text{2}}}\\ =5\text{m}\end{array}$

Write the formula to calculate the electrical force

    $F_{BC}=\frac{k_e{q}_1{q}_2}{r^2}$

Here, $k_e$ is the constant, $q_1$ is the charge on particle $B$, $q_2$ is the charge on particle $C$ and $r$ is the distance between the particles $B$ and $C$.

Substitute $-6.00\times {10}^{-4}\text{C}$ for $q_1$, $1.00\times {10}^{-4}\text{C}$ for $q_2$, $5.00\text{m}$ to find $F_{BC}$ as,

    $\begin{array}{c}{F}_{BC}=\frac{k_e{q}_1{q}_2}{r^2}\\ =\frac{\left(9\times {10}^9\text{N}\cdot {\text{m}}^2/{\text{C}}^2\right)\left(-6.00\times {10}^{-4}\text{C}\right)\left(1.00\times {10}^{-4}\text{C}\right)}{{\left(5.00\text{m}\right)}^2}\\ =-21.6\text{N}\\ \left|F_{\text{BC}}\right|=21.6\text{N}\end{array}$

Conclusion:

Therefore, the magnitude of the force exerted by $B$ on $C$ $21.6\text{N}$.

To determine

The $x-$ component of the force exerted by $B$ on $C$.

Answer to Problem 23.18P

The $x-$ component of the force exerted by $B$ on $C$ is $17.3\text{N}$.

Explanation of Solution

From part (c), the magnitude of the force exerted by $B$ on $C$ is $21.6\text{N}$.

Resolve the side $BC$ into horizontal and vertical components as- horizontal component is $\left|F_{BC}\right|\cos \alpha$ and vertical component is $\left|F_{\text{BC}}\right|\sin \text{}\alpha$

From Figure I

    $\cos \alpha =\frac{4}{5}$

Here, $\alpha$ is the angle between the x-axis and the line joining the charges $B$ and $C$.

Write the formula to calculate the $x-$ component of force by $B$ on $C$

    $F_{\text{xBC}}=\left|F_{\text{BC}}\right|\cos \alpha$

Here, $\left|F_{\text{BC}}\right|$ is the force exerted by $B$ on $C$ and $\cos \alpha$ is the horizontal component of $BC$.

Substitute $21.6\text{N}$ for $\left|F_{\text{BC}}\right|$ and $\frac{4}{5}$ for $\cos \alpha$ to calculate $F_{\text{xBC}}$ as,

    $\begin{array}{c}{F}_{\text{xBC}}=\left|F_{\text{BC}}\right|\cos \alpha \\ =\left(21.6\text{}\text{N}\right)\left(\frac{4}{5}\right)\\ =17.28\text{N}\\ \approx 17.3\text{N}\end{array}$

Conclusion:

Therefore, the $x-$ component of the force exerted by $B$ on $C$ is $17.3\text{N}$.

To determine

The $y-$ component of the force exerted by $B$ on $C$.

Answer to Problem 23.18P

The $y-$ component of the force exerted by $B$ on $C$ is $-13.0\text{N}$.

Explanation of Solution

From part (c), the magnitude of the force exerted by $B$ on $C$ is $21.6\text{N}$.

Resolve the side $BC$ into horizontal and vertical components as-the horizontal component is $\left|F_{\text{BC}}\right|\cos \alpha$ and vertical component is $\left|F_{\text{BC}}\right|\sin \text{}\alpha$

From Figure I,

    $\sin \alpha =\frac{3}{5}$

Write the formula to calculate the $y-$ component of force by $B$ $C$

    $F_{\text{yBC}}=-\left|F_{\text{BC}}\right|\sin \alpha$

Here, $\left|F_{BC}\right|$ is the force exerted by $B$ on $C$ and $\sin \alpha$ is the vertical component of $BC$.

Substitute $21.6\text{N}$ for $\left|F_{\text{BC}}\right|$ and $\frac{3}{5}$ for $\sin \alpha$ in the above formula as,

    $\begin{array}{c}{F}_{\text{yBC}}=-\left|F_{\text{BC}}\right|\sin \alpha \\ =-\left(21.6\text{}\text{N}\right)\left(\frac{3}{5}\right)\\ =-12.96\text{N}\\ \approx -13.0\text{}\text{N}\end{array}$

Conclusion:

Therefore, the $y-$ component of the force exerted by $B$ on $C$ is $-13.0\text{N}$.

To determine

The resultant $x-$ component of the electric force acting on $C$.

Answer to Problem 23.18P

The resultant $x-$ component of the electric force acting on $C$ is $17.3\text{N}$

Explanation of Solution

From part (a), the $x-$ component of the force exerted by $A$ on $C$

    $\left|F_{\text{xAC}}\right|=0$

From part (d), the $x-$ component of the force exerted by $B$ on $C$

    $\left|F_{\text{xBC}}\right|=17.28\text{N}$

Write the formula to calculate the resultant force acting on the particle $C$

    $F_{\text{xC}}=F_{\text{xAC}}+F_{\text{xBC}}$

Here, $F_{\text{xC}}$ is the sum of $x-$ component of the force acting on $C$, $F_{\text{xAC}}$ is the $x-$ component of the force exerted by $A$ on $C$ and $F_{\text{xBC}}$ is the $x-$ component of the force exerted by $B$ on $C$.

Substitute $0$ for $\left|F_{\text{xAC}}\right|$ and $17.3\text{N}$ for $\left|F_{\text{xBC}}\right|$ to calculate $F_{\text{xC}}$ as,

    $\begin{array}{c}{F}_{\text{xC}}=F_{\text{xAC}}+F_{\text{xBC}}\\ =0+17.3\text{N}\\ \text{=17}\text{.3}\text{N}\end{array}$

Conclusion:

Therefore, the resultant $x-$ component of the electric force acting on $C$ is $17.3\text{N}$.

To determine

The resultant $y-$ component of the electric force acting on $C$.

Answer to Problem 23.18P

The resultant $y-$ component of the electric force acting on $C$ is $17.0\text{N}$

Explanation of Solution

From part (b), the $y-$ component of the force exerted by $A$ on $C$

    $\left|F_{\text{yAC}}\right|=30\text{N}$

From part (e), the $y-$ component of the force exerted by $B$ on $C$

    $\left|F_{\text{yBC}}\right|=17.28\text{N}$

Write the formula to calculate the resultant force acting on the particle $C$

    $F_{\text{yC}}=F_{\text{yAC}}+F_{\text{yBC}}$

Here, $F_{\text{yC}}$ is the sum of $y-$ component of the force acting on $C$, $F_{\text{yAC}}$ is the $y-$ component of the force exerted by $A$ on $C$ and $F_{\text{yBC}}$ is the $y-$ component of the force exerted by $B$ on $C$.

Substitute $30\text{N}$ for $\left|F_{\text{yAC}}\right|$ and $-13.0\text{N}$ for $\left|F_{\text{yBC}}\right|$ to calculate $F_{\text{yC}}$ as,

    $\begin{array}{c}{F}_{\text{yC}}=F_{\text{yAC}}+F_{\text{yBC}}\\ =30\text{N}-13.0\text{N}\\ =\text{17}\text{.0}\text{N}\end{array}$

Conclusion:

Therefore, the resultant $y-$ component of the electric force acting on $C$ is $17.0\text{N}$.

To determine

The magnitude and direction of the resultant electric force acting on $C$

Answer to Problem 23.18P

The magnitude and direction of the resultant electric force acting on $C$ is $24.3\text{N}$ and at an angle $44.5°$ with the x-axis.

Explanation of Solution

From part (g), the resultant $y-$ component of the electric force acting on $C$ is $42.96\text{N}$.

    $\left|F_{\text{yC}}\right|=42.96\text{N}$

From part (f), the resultant $x-$ component of the electric force acting on $C$

    $\left|F_{\text{xC}}\right|=17.28\text{N}$

Write the formula to calculate the resultant force acting on the particle $C$

    $F_{\text{C}}=\sqrt{F^2{}_{\text{yC}}+F^2{}_{\text{xC}}}$

Here, $F_{\text{C}}$ is the resultant force acting on $C$, $F_{\text{yC}}$ is the resultant $y-$ component of the force exerted by $A$ on $C$ and $F_{\text{xC}}$ is the $x-$ component of the force exerted by $B$ on $C$.

Substitute $17.0\text{N}$ for $\left|F_{\text{yC}}\right|$ and $17.3\text{N}$ for $\left|F_{\text{xC}}\right|$ to calculate $F_{\text{C}}$  as,

    $\begin{array}{c}{F}_{\text{C}}=\sqrt{F^2{}_{\text{yC}}+F^2{}_{\text{xC}}}\\ =\sqrt{{\left(17.0\text{N}\right)}^2+{\left(17.3\text{N}\right)}^2}\\ =24.3\text{N}\end{array}$

Write the formula to calculate the direction of the resultant force acting on $C$

    $\theta ={\tan }^{-1}\left(\frac{F_{\text{yC}}}{F_{\text{xC}}}\right)$

Here, $F_{\text{y}}$ is the resultant $y-$ component force acting on the particle $C$ and $F_{\text{x}}$ is the resultant $x-$ component force acting on the particle $C$.

Substitute $17.0\text{N}$ for $F_{\text{yC}}$ and $17.3\text{N}$ for $F_{\text{xC}}$ to calculate $\theta$

    $\begin{array}{c}\theta ={\tan }^{-1}\left(\frac{F_{yC}}{F_{xC}}\right)\\ ={\tan }^{-1}\left(\frac{17.0\text{N}}{17.3\text{N}}\right)\\ =44.5°\end{array}$

The direction of the resultant force is counterclockwise from $+x$ axis.

Conclusion:

Therefore, the magnitude and direction of the resultant electric force acting on $C$ is $24.3\text{N}$ and at an angle $44.5°$ with the x-axis.