ALEKS 360 ACCESS CARD PRECALCULUS 18 WK
1st Edition
ISBN: 9781265748456
Author: Miller
Publisher: MCGRAW-HILL HIGHER EDUCATION
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2.2, Problem 99PE
A solar oven is to be made from an open box with reflective sides. Each box is made from a 30-in. by 24-in. rectangular sheet of aluminium with square of length x (in inches) removed from each corner. Then the flaps are folder up to form an open box.
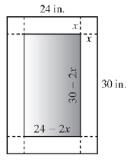
a. Show that the volume of the box is given by
b. Graph the function from part (a) and a “maximum� feature on a graphing utility to approximate the length of the sides of the squares that should be removed to maximize the volume. Round to the nearest tenth of an inch.
c. Approximate the maximum volume. Round to the nearest cubic inch.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
5. For the function y-x³-3x²-1, use
derivatives to:
(a) determine the intervals of increase and
decrease.
(b) determine the local (relative) maxima and
minima.
(e) determine the intervals of concavity.
(d) determine the points of inflection.
(e) sketch the graph with the above information
indicated on the graph.
Can you solve this 2 question numerical method
1. Estimate the area under the graph of
f(x)-25-x from x=0 to x=5 using 5
approximating rectangles Using:
(A) right endpoints.
(B) left endpoints.
Chapter 2 Solutions
ALEKS 360 ACCESS CARD PRECALCULUS 18 WK
Ch. 2.1 - Repeat Example 1 with gx=x+221.Ch. 2.1 - Prob. 2SPCh. 2.1 - Repeat Example 3 with fx=x24x7.Ch. 2.1 - A quarterback throws a football with an initial...Ch. 2.1 - Prob. 5SPCh. 2.1 - The funding ftin$millions for a drug...Ch. 2.1 - A function defined by fx=ax2+bx+ca0 is called a ...Ch. 2.1 - The vertical line drawn through the vertex of a...Ch. 2.1 - Given fx=axh2+ka0, the vertex of the parabola is...Ch. 2.1 - Given fx=axh2+k,ifa0, the parabola opens...
Ch. 2.1 - Given fx=axh2+k,ifa0, the parabola opens...Ch. 2.1 - The graph of fx=axh2+k,a0, is a parabola and the...Ch. 2.1 - For Exercises 7-14, a. Determine whether the graph...Ch. 2.1 - For Exercises 7-14, a. Determine whether the graph...Ch. 2.1 - For Exercises 7-14, a. Determine whether the graph...Ch. 2.1 - Prob. 10PECh. 2.1 - For Exercises 7-14, a. Determine whether the graph...Ch. 2.1 - For Exercises 7-14, a. Determine whether the graph...Ch. 2.1 - For Exercises 7-14, a. Determine whether the graph...Ch. 2.1 - Prob. 14PECh. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 15-24, a. Write the function in...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 25-32, find the vertex of the...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - For Exercises 33-42, a. State whether the graph of...Ch. 2.1 - The monthly profit for a small company that makes...Ch. 2.1 - The monthly profit fora company that makes...Ch. 2.1 - A long jumper leaves the ground at an angle of 20o...Ch. 2.1 - A firefighter holds a hose 3 m off the ground and...Ch. 2.1 - The population pt of a culture of the bacterium...Ch. 2.1 - The gas mileage mx (in mpg) for a certain vehicle...Ch. 2.1 - The sum of two positive numbers is 24. What two...Ch. 2.1 - The sum of two positive numbers is 1. What two...Ch. 2.1 - The difference of two numbers is 10. What two...Ch. 2.1 - Prob. 52PECh. 2.1 - Suppose that a family wants to fence in an area of...Ch. 2.1 - Two chicken coops are to be built adjacent to one...Ch. 2.1 - A trough at the end of a gutter spout is meant to...Ch. 2.1 - Prob. 56PECh. 2.1 - Tetanus bacillus bacteria are cultured to produce...Ch. 2.1 - Gas mileage is tested for a car under different...Ch. 2.1 - Fluid runs through a drainage pipe with a 10-cm...Ch. 2.1 - The braking distance required for a car to stop...Ch. 2.1 - For Exercises 61-64, given a quadratic function...Ch. 2.1 - For Exercises 61-64, given a quadratic function...Ch. 2.1 - Prob. 63PECh. 2.1 - For Exercises 61-64, given a quadratic function...Ch. 2.1 - For Exercises 65-70, determine the number of...Ch. 2.1 - Prob. 66PECh. 2.1 - For Exercises 65-70, determine the number of...Ch. 2.1 - For Exercises 65-70, determine the number of...Ch. 2.1 - For Exercises 65-70, determine the number of...Ch. 2.1 - For Exercises 65-70, determine the number of...Ch. 2.1 - For Exercises 71-78, given a quadratic function...Ch. 2.1 - Prob. 72PECh. 2.1 - Prob. 73PECh. 2.1 - For Exercises 71-78, given a quadratic function...Ch. 2.1 - For Exercises 71-78, given a quadratic function...Ch. 2.1 - For Exercises 71-78, given a quadratic function...Ch. 2.1 - For Exercises 71-78, given a quadratic function...Ch. 2.1 - Prob. 78PECh. 2.1 - Prob. 79PECh. 2.1 - Prob. 80PECh. 2.1 - Prob. 81PECh. 2.1 - Explain how to use the discriminant to determine...Ch. 2.1 - Prob. 83PECh. 2.1 - Prob. 84PECh. 2.1 - For Exercises 85-88, define a quadratic function...Ch. 2.1 - For Exercises 85-88, define a quadratic function...Ch. 2.1 - For Exercises 85-88, define a quadratic function...Ch. 2.1 - For Exercises 85-88, define a quadratic function...Ch. 2.1 - For Exercises 89-92, find the value of b or c that...Ch. 2.1 - For Exercises 89-92, find the value of b or c that...Ch. 2.1 - Prob. 91PECh. 2.1 - For Exercises 89-92, find the value of b or c that...Ch. 2.2 - Use the leading term to determine the end...Ch. 2.2 - Find the zeros of the function defined by...Ch. 2.2 - Find the zeros of the function defined by...Ch. 2.2 - Determine the zeros and their multiplicities for...Ch. 2.2 - Show that fx=x4+6x326x+15 has a zero on the...Ch. 2.2 - Graph gx=x3+4x.Ch. 2.2 - Graph hx=0.5xx1x+32.Ch. 2.2 - A function defined by...Ch. 2.2 - The function given by fx=3x5+2x+12x (is/is not) a...Ch. 2.2 - The function given by fx=3x5+2x+2x (is/is not) a...Ch. 2.2 - A quadratic function is a polynomial function of...Ch. 2.2 - A linear function is a polynomial function of...Ch. 2.2 - The values of x in the domain of a polynomial...Ch. 2.2 - What is the maximum number of turning points of...Ch. 2.2 - If the graph of a polynomial function has 3...Ch. 2.2 - If c is a real zero of a polynomial function and...Ch. 2.2 - If c is a real zero of a polynomial function and...Ch. 2.2 - Prob. 11PECh. 2.2 - What is the leading term of fx=13x343x+52?Ch. 2.2 - Prob. 13PECh. 2.2 - For Exercises 13-20, determine the end behavior of...Ch. 2.2 - For Exercises 13-20, determine the end behavior of...Ch. 2.2 - For Exercises 13-20, determine the end behavior of...Ch. 2.2 - Prob. 17PECh. 2.2 - For Exercises 13-20, determine the end behavior of...Ch. 2.2 - For Exercises 13-20, determine the end behavior of...Ch. 2.2 - For Exercises 13-20, determine the end behavior of...Ch. 2.2 - Given the function defined by gx=3x13x+54, the...Ch. 2.2 - Given the function defined by hx=12x5x+0.63, the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - Prob. 28PECh. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - Prob. 32PECh. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - Prob. 36PECh. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - For Exercises 23-38, find the zeros of the...Ch. 2.2 - Prob. 39PECh. 2.2 - For Exercises 39-40, determine whether the...Ch. 2.2 - For Exercises 41-42, a table of values is given...Ch. 2.2 - For Exercises 41-42, a table of values is given...Ch. 2.2 - Given fx=4x38x225x+50, a. Determine if f has a...Ch. 2.2 - Prob. 44PECh. 2.2 - For Exercises 45-52, determine if the graph can...Ch. 2.2 - Prob. 46PECh. 2.2 - For Exercises 45-52, determine if the graph can...Ch. 2.2 - Prob. 48PECh. 2.2 - For Exercises 45-52, determine if the graph can...Ch. 2.2 - Prob. 50PECh. 2.2 - For Exercises 45-52, determine if the graph can...Ch. 2.2 - For Exercises 45-52, determine if the graph can...Ch. 2.2 - Prob. 53PECh. 2.2 - For Exercises 53-58, a. Identify the power...Ch. 2.2 - For Exercises 53-58, a. Identify the power...Ch. 2.2 - Prob. 56PECh. 2.2 - For Exercises 53-58, a. Identify the power...Ch. 2.2 - Prob. 58PECh. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - Prob. 61PECh. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - Prob. 67PECh. 2.2 - Prob. 68PECh. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - Prob. 70PECh. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - Prob. 74PECh. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 59-76, sketch the function. (See...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - For Exercises 77-88, determine if the statement is...Ch. 2.2 - A rocket will carry a communications satellite...Ch. 2.2 - Data from a 20-yr study show the number of new...Ch. 2.2 - Given a polynomial function defined by y=fx,...Ch. 2.2 - Given a polynomial function, explain how to...Ch. 2.2 - Prob. 93PECh. 2.2 - Prob. 94PECh. 2.2 - Use this broader statement of the intermediate...Ch. 2.2 - Use this broader statement of the intermediate...Ch. 2.2 - For a certain individual the volume (in liters) of...Ch. 2.2 - The torque (in ft-lb) produced a certain...Ch. 2.2 - A solar oven is to be made from an open box with...Ch. 2.2 - For Exercises 100-101, two viewing windows are...Ch. 2.2 - For Exercises 100-101, two viewing windows are...Ch. 2.2 - For Exercises 102-103, graph the function defined...Ch. 2.2 - For Exercises 102-103, graph the function defined...Ch. 2.3 - Use long division to divide 4x323x+32x5.Ch. 2.3 - Use long division to divide. 17x+5x23x3+2x4x2+3Ch. 2.3 - Use long division to divide. 3x214x+15x3Ch. 2.3 - Use synthetic division to divide. 4x328x7x3Ch. 2.3 - Use synthetic division to divide. 3x+7x3+5+2x4x+1Ch. 2.3 - Given fx=x4+x36x25x15, use the remainder theorem...Ch. 2.3 - Use the remainder theorem to determine if the...Ch. 2.3 - Use the factor theorem to determine if the given...Ch. 2.3 - a. Factor fx=2x3+7x214x40, given that 4 is a zero...Ch. 2.3 - Write a polynomial fx of degree 3 that has the...Ch. 2.3 - Given the division algorithm, identify the...Ch. 2.3 - Given 2x35x26x+1x3=2x2+x3+8x3, use the division...Ch. 2.3 - The remainder theorem indicates that if a...Ch. 2.3 - Given a polynomial fx, the factor theorem...Ch. 2.3 - Answer true or false. If 5 is a zero of a...Ch. 2.3 - Answer true or false. If x+3 is a factor of a...Ch. 2.3 - For Exercises 7-8, (See Example 1) a. Use long...Ch. 2.3 - Prob. 8PECh. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - Prob. 18PECh. 2.3 - Prob. 19PECh. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 9-22, use long division to divide....Ch. 2.3 - For Exercises 23-26, consider the division of two...Ch. 2.3 - Prob. 24PECh. 2.3 - For Exercises 23-26, consider the division of two...Ch. 2.3 - Prob. 26PECh. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - Prob. 28PECh. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - Prob. 34PECh. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - For Exercises 27-38, use synthetic division to...Ch. 2.3 - The value f6=39 for a polynomial fx . What can be...Ch. 2.3 - Given a polynomial fx, the quotient fxx2 has a...Ch. 2.3 - Given fx=2x45x3+x27, a. Evaluate f4 . b. Determine...Ch. 2.3 - Given gx=3x5+2x4+6x2x+4, a. Evaluate g2 b....Ch. 2.3 - For Exercises 43-46, use the remainder theorem to...Ch. 2.3 - For Exercises 43-46, use the remainder theorem to...Ch. 2.3 - For Exercises 43-46, use the remainder theorem to...Ch. 2.3 - For Exercises 43-46, use the remainder theorem to...Ch. 2.3 - For Exercises 47-54, use the reminder theorem to...Ch. 2.3 - For Exercises 47-54, use the reminder theorem to...Ch. 2.3 - For Exercises 47-54, use the reminder theorem to...Ch. 2.3 - For Exercises 47-54, use the reminder theorem to...Ch. 2.3 - For Exercises 47-54, use the reminder theorem to...Ch. 2.3 - Prob. 52PECh. 2.3 - Prob. 53PECh. 2.3 - For Exercises 47-54, use the reminder theorem to...Ch. 2.3 - For Exercises 55-60, use the factor theorem to...Ch. 2.3 - For Exercises 55-60, use the factor theorem to...Ch. 2.3 - For Exercises 55-60, use the factor theorem to...Ch. 2.3 - For Exercises 55-60, use the factor theorem to...Ch. 2.3 - For Exercises 55-60, use the factor theorem to...Ch. 2.3 - Prob. 60PECh. 2.3 - Given gx=x414x2+45, a. Evaluate g5. b. Evaluate...Ch. 2.3 - Given hx=x415x2+44, a. Evaluate h11. b. Evaluate...Ch. 2.3 - Prob. 63PECh. 2.3 - Prob. 64PECh. 2.3 - a. Factor fx=2x3+x237x36, given that 1 is a zero....Ch. 2.3 - a. Factor fx=3x3+16x25x50, given that 2 is a zero....Ch. 2.3 - a. Factor fx=20x3+39x23x2, given that 14 is a...Ch. 2.3 - a. Factor fx=8x318x211x+15, given that 34 is a...Ch. 2.3 - a. Factor fx=9x333x2+19x3, given that 3 is a zero....Ch. 2.3 - Prob. 70PECh. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - Prob. 72PECh. 2.3 - Prob. 73PECh. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - Prob. 75PECh. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - Prob. 79PECh. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - Prob. 81PECh. 2.3 - For Exercises 71-82, write a polynomial fx that...Ch. 2.3 - Prob. 83PECh. 2.3 - Prob. 84PECh. 2.3 - ...Ch. 2.3 - If a fifth-degree polynomial is divided by a...Ch. 2.3 - Determine if the statement is true or false: Zero...Ch. 2.3 - Determine if the statement is true or false: Zero...Ch. 2.3 - Find m so that x+4 is a factor of 4x3+13x25x+m.Ch. 2.3 - Find m so that x+5 is a factor of...Ch. 2.3 - Find m so that x+2 is a factor of 4x3+5x2+mx+2.Ch. 2.3 - Prob. 92PECh. 2.3 - Prob. 93PECh. 2.3 - For what value of r is the statement an identify?...Ch. 2.3 - A metal block is formed from a rectangular solid...Ch. 2.3 - A wedge is cut from a rectangular solid. a. Write...Ch. 2.3 - Under what circumstances can synthetic division be...Ch. 2.3 - How can the division algorithm be used to check...Ch. 2.3 - Given a polynomial fx and a constant c, state two...Ch. 2.3 - Write an informal explanation of the factor...Ch. 2.3 - a. Factor fx=x35x2+x5 into factors of the form xc,...Ch. 2.3 - a. Factor fx=x33x2+100x300 into factors of the...Ch. 2.3 - a. Factor fx=x4+2x32x26x3 into factors of the form...Ch. 2.3 - a. Factor fx=x4+4x3x220x20 into factors of the...Ch. 2.3 - For Exercises 105-106, a. Use the graph to...Ch. 2.3 - For Exercises 105-106, a. Use the graph to...Ch. 2.4 - List all possible rational Zeros. fx=4x4+5x37x2+8Ch. 2.4 - Find the zeros. fx=x3x24x2Ch. 2.4 - Prob. 3SPCh. 2.4 - Prob. 4SPCh. 2.4 - Given fx=x42x3+28x24x+52, and that 1+5i is a zero...Ch. 2.4 - a. Find a third-degree polynomial fx with integer...Ch. 2.4 - Determine the number of possible positive and...Ch. 2.4 - Determine the number of possible positive and...Ch. 2.4 - Prob. 9SPCh. 2.4 - Find the zeros and their multiplicities....Ch. 2.4 - The of a polynomial fx are the solutions (or...Ch. 2.4 - If fx is a polynomial of degree n1 with complex...Ch. 2.4 - The conjugate zeros theorem states that if fx is a...Ch. 2.4 - A real number b is called an bound of the real...Ch. 2.4 - A real number a is called a lower bound of the...Ch. 2.4 - Explain why the number 7 cannot be a rational zero...Ch. 2.4 - For Exercises 7-12, list the possible rational...Ch. 2.4 - Prob. 8PECh. 2.4 - For Exercises 7-12, list the possible rational...Ch. 2.4 - For Exercises 7-12, list the possible rational...Ch. 2.4 - For Exercises 7-12, list the possible rational...Ch. 2.4 - For Exercises 7-12, list the possible rational...Ch. 2.4 - Prob. 13PECh. 2.4 - Which of the following is not a possible zero of...Ch. 2.4 - Prob. 15PECh. 2.4 - For Exercises 15-16, find all the rational zeros....Ch. 2.4 - Prob. 17PECh. 2.4 - Prob. 18PECh. 2.4 - For Exercises 17-28, find all the zeros. (See...Ch. 2.4 - For Exercises 17-28, find all the zeros. (See...Ch. 2.4 - Prob. 21PECh. 2.4 - Prob. 22PECh. 2.4 - Prob. 23PECh. 2.4 - For Exercises 17-28, find all the zeros. (See...Ch. 2.4 - For Exercises 17-28, find all the zeros. (See...Ch. 2.4 - Prob. 26PECh. 2.4 - For Exercises 17-28, find all the zeros. (See...Ch. 2.4 - For Exercises 17-28, find all the zeros. (See...Ch. 2.4 - Given a polynomial fx of degree n1, the...Ch. 2.4 - Prob. 30PECh. 2.4 - If fx is a polynomial with real coefficients and...Ch. 2.4 - If gx is a polynomial with real coefficients and...Ch. 2.4 - For Exercises 33-38, a polynomial fx and one or...Ch. 2.4 - For Exercises 33-38, a polynomial fx and one or...Ch. 2.4 - For Exercises 33-38, a polynomial fx and one or...Ch. 2.4 - Prob. 36PECh. 2.4 - Prob. 37PECh. 2.4 - For Exercises 33-38, a polynomial fx and one or...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - Prob. 45PECh. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 39-48, write a polynomial fx that...Ch. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - Prob. 51PECh. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - For Exercises 49-56, determine the number of...Ch. 2.4 - For Exercises 57-58, use Descartes’ rule of...Ch. 2.4 - For Exercises 57-58, use Descartes’ rule of...Ch. 2.4 - For Exercises 59-64, (See Example 9) a. Determine...Ch. 2.4 - For Exercises 59-64, (See Example 9) a. Determine...Ch. 2.4 - For Exercises 59-64, (See Example 9) a. Determine...Ch. 2.4 - For Exercises 59-64, (See Example 9) a. Determine...Ch. 2.4 - For Exercises 59-64, (See Example 9) a. Determine...Ch. 2.4 - Prob. 64PECh. 2.4 - For Exercises 65-68, determine if the statement is...Ch. 2.4 - For Exercises 65-68, determine if the statement is...Ch. 2.4 - For Exercises 65-68, determine if the statement is...Ch. 2.4 - For Exercises 65-68, determine if the statement is...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - Prob. 76PECh. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - Prob. 78PECh. 2.4 - Prob. 79PECh. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 69-84, find the zeros and their...Ch. 2.4 - For Exercises 85-90, determine if the statement is...Ch. 2.4 - For Exercises 85-90, determine if the statement is...Ch. 2.4 - For Exercises 85-90, determine if the statement is...Ch. 2.4 - Prob. 88PECh. 2.4 - For Exercises 85-90, determine if the statement is...Ch. 2.4 - For Exercises 85-90, determine if the statement is...Ch. 2.4 - Given that xc divides evenly into a polynomial fx...Ch. 2.4 - a. Use the quadratic formula to solve x27x+5=0. b....Ch. 2.4 - a. Use the intermediate value theorem to show that...Ch. 2.4 - Show that xa is a factor of xnan for any positive...Ch. 2.4 - Explain why a polynomial with real coefficients of...Ch. 2.4 - Why is it not necessary to apply the rational zero...Ch. 2.4 - Prob. 97PECh. 2.4 - Explain why the fundamental theorem of algebra...Ch. 2.4 - Let n be a positive even integer. Determine the...Ch. 2.4 - Let n be a positive odd integer. Determine the...Ch. 2.4 - The front face of a tent is triangular and the...Ch. 2.4 - An underground storage tank for gasoline is in the...Ch. 2.4 - A food company originally sells cereal in boxes...Ch. 2.4 - Prob. 104PECh. 2.4 - A rectangle is bounded by the x-axis and a...Ch. 2.4 - A rectangle is bounded by the parabola defined by...Ch. 2.4 - For Exercises 107-110, a. Factor the polynomial...Ch. 2.4 - For Exercises 107-110, a. Factor the polynomial...Ch. 2.4 - Prob. 109PECh. 2.4 - For Exercises 107-110, a. Factor the polynomial...Ch. 2.4 - Find all fourth roots of 1, by solving the...Ch. 2.4 - Find all sixth roots of 1, by solving the equation...Ch. 2.4 - Prob. 113PECh. 2.4 - Prob. 114PECh. 2.4 - For Exercises 115-116, use the formula...Ch. 2.4 - For Exercises 115-116, use the formula...Ch. 2.5 - The graph of is given. fx=1x2 Complete the...Ch. 2.5 - Identify the vertical asymptotes....Ch. 2.5 - Prob. 3SPCh. 2.5 - Given gx=3x2+4x3x2+3 , determine the horizontal...Ch. 2.5 - Prob. 5SPCh. 2.5 - Use transformations to graph gx=1x32.Ch. 2.5 - Graph fx=x1x+4.Ch. 2.5 - Graph gx=5xx29.Ch. 2.5 - Prob. 9SPCh. 2.5 - Prob. 10SPCh. 2.5 - Repeat Example 11 under the assumption that the...Ch. 2.5 - The domain of a rational function defined by...Ch. 2.5 - The notation x is read as .Ch. 2.5 - The notation x5 is read as .Ch. 2.5 - Prob. 4PECh. 2.5 - Prob. 5PECh. 2.5 - Prob. 6PECh. 2.5 - Prob. 7PECh. 2.5 - Prob. 8PECh. 2.5 - Prob. 9PECh. 2.5 - Prob. 10PECh. 2.5 - Prob. 11PECh. 2.5 - Prob. 12PECh. 2.5 - For Exercises 13-16, refer to the graph of the...Ch. 2.5 - For Exercises 13-16, refer to the graph of the...Ch. 2.5 - Prob. 15PECh. 2.5 - Prob. 16PECh. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - For Exercises 17-24, determine the vertical...Ch. 2.5 - The graph of fx=x2+82x23 will behave like which...Ch. 2.5 - The graph of fx=2x3+75x3 will behave like which...Ch. 2.5 - The graph of fx=3x42x+5x5+x22 will behave like...Ch. 2.5 - Prob. 28PECh. 2.5 - Prob. 29PECh. 2.5 - For Exercises 29-36, a. Identify the horizontal...Ch. 2.5 - For Exercises 29-36, a. Identify the horizontal...Ch. 2.5 - For Exercises 29-36, a. Identify the horizontal...Ch. 2.5 - Prob. 33PECh. 2.5 - For Exercises 29-36, a. Identify the horizontal...Ch. 2.5 - Prob. 35PECh. 2.5 - Prob. 36PECh. 2.5 - Prob. 37PECh. 2.5 - Prob. 38PECh. 2.5 - Prob. 39PECh. 2.5 - Prob. 40PECh. 2.5 - Prob. 41PECh. 2.5 - For Exercises 39-48, identify the asymptotes. (See...Ch. 2.5 - Prob. 43PECh. 2.5 - Prob. 44PECh. 2.5 - Prob. 45PECh. 2.5 - Prob. 46PECh. 2.5 - Prob. 47PECh. 2.5 - Prob. 48PECh. 2.5 - Prob. 49PECh. 2.5 - Prob. 50PECh. 2.5 - For Exercises 49-56, graph the functions by using...Ch. 2.5 - For Exercises 49-56, graph the functions by using...Ch. 2.5 - For Exercises 49-56, graph the functions by using...Ch. 2.5 - For Exercises 49-56, graph the functions by using...Ch. 2.5 - Prob. 55PECh. 2.5 - Prob. 56PECh. 2.5 - For Exercises 57-62, for the graph of y=fx. a....Ch. 2.5 - Prob. 58PECh. 2.5 - For Exercises 57-62, for the graph of y=fx. a....Ch. 2.5 - Prob. 60PECh. 2.5 - For Exercises 57-62, for the graph of y=fx. a....Ch. 2.5 - Prob. 62PECh. 2.5 - For Exercises 63-66, sketch a rational function...Ch. 2.5 - Prob. 64PECh. 2.5 - For Exercises 63-66, sketch a rational function...Ch. 2.5 - Prob. 66PECh. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - Prob. 77PECh. 2.5 - Prob. 78PECh. 2.5 - Prob. 79PECh. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - Prob. 81PECh. 2.5 - Prob. 82PECh. 2.5 - Prob. 83PECh. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - Prob. 85PECh. 2.5 - Prob. 86PECh. 2.5 - Prob. 87PECh. 2.5 - For Exercises 67-90, graph the function. (See...Ch. 2.5 - Prob. 89PECh. 2.5 - Prob. 90PECh. 2.5 - Prob. 91PECh. 2.5 - An on-demand printing company has monthly overhead...Ch. 2.5 - Prob. 93PECh. 2.5 - Prob. 94PECh. 2.5 - Prob. 95PECh. 2.5 - A certain diet pill is designed to delay the...Ch. 2.5 - A power company burns coal to generate...Ch. 2.5 - The cost Cxin$1000 for a city to remove x of the...Ch. 2.5 - Prob. 99PECh. 2.5 - The Doppler effect is a change in the observed...Ch. 2.5 - Prob. 101PECh. 2.5 - Prob. 102PECh. 2.5 - Prob. 103PECh. 2.5 - Prob. 104PECh. 2.5 - Prob. 105PECh. 2.5 - Prob. 106PECh. 2.5 - Prob. 107PECh. 2.5 - Prob. 108PECh. 2.5 - Prob. 109PECh. 2.5 - Prob. 110PECh. 2.5 - Prob. 111PECh. 2.5 - Prob. 112PECh. 2.5 - Prob. 113PECh. 2.5 - The rational functions studied in this section all...Ch. 2.5 - For Exercises 1-8, refer to...Ch. 2.5 - For Exercises 1-8, refer to...Ch. 2.5 - For Exercises 1-8, refer to...Ch. 2.5 - Prob. 4PRECh. 2.5 - For Exercises 1-8, refer to...Ch. 2.5 - Prob. 6PRECh. 2.5 - For Exercises 1-8, refer to...Ch. 2.5 - Prob. 8PRECh. 2.5 - For Exercises 9-16, refer to...Ch. 2.5 - Prob. 10PRECh. 2.5 - Prob. 11PRECh. 2.5 - Prob. 12PRECh. 2.5 - For Exercises 9-16, refer to...Ch. 2.5 - For Exercises 9-16, refer to...Ch. 2.5 - Prob. 15PRECh. 2.5 - For Exercises 9-16, refer to...Ch. 2.5 - For Exercises 17-18, use the results from...Ch. 2.5 - For Exercises 17-18, use the results from...Ch. 2.5 - Divide 2x34x210x+12x211 by using an appropriate...Ch. 2.5 - Identify the slant asymptote of fx=2x34x210+12x211...Ch. 2.5 - Identify the point where the graph of...Ch. 2.5 - Refer to Exercise 19. Solve the equation rx=0. How...Ch. 2.6 - Solve the inequality. 2xx121xCh. 2.6 - Solve the inequality. x418x3x24x3Ch. 2.6 - Prob. 3SPCh. 2.6 - Solve the inequality. 5xx12Ch. 2.6 - Prob. 5SPCh. 2.6 - Solve the inequalities....Ch. 2.6 - Repeat Example 7 under the assumption that the...Ch. 2.6 - Let fx be a polynomial. An inequality of the form...Ch. 2.6 - Let fx be a rational expression. An inequality of...Ch. 2.6 - The solution set for the inequality x+1024 is ,...Ch. 2.6 - The solutions to an inequality fx0 are the values...Ch. 2.6 - Prob. 5PECh. 2.6 - For Exercises 5-14, the graph of y=fx is given....Ch. 2.6 - Prob. 7PECh. 2.6 - Prob. 8PECh. 2.6 - For Exercises 5-14, the graph of y=fx is given....Ch. 2.6 - Prob. 10PECh. 2.6 - For Exercises 5-14, the graph of y=fx is given....Ch. 2.6 - For Exercises 5-14, the graph of y=fx is given....Ch. 2.6 - For Exercises 5-14, the graph of y=fx is given....Ch. 2.6 - Prob. 14PECh. 2.6 - Prob. 15PECh. 2.6 - For Exercises 15-20, solve the equations and...Ch. 2.6 - For Exercises 15-20, solve the equations and...Ch. 2.6 - For Exercises 15-20, solve the equations and...Ch. 2.6 - For Exercises 15-20, solve the equations and...Ch. 2.6 - For Exercises 15-20, solve the equations and...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - Prob. 49PECh. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 21-54, solve the inequalities. (See...Ch. 2.6 - For Exercises 55-58, the graph of y=fx is given....Ch. 2.6 - For Exercises 55-58, the graph of y=fx is given....Ch. 2.6 - Prob. 57PECh. 2.6 - For Exercises 55-58, the graph of y=fx is given....Ch. 2.6 - Prob. 59PECh. 2.6 - For Exercises 59-62, solve the inequalities. (See...Ch. 2.6 - For Exercises 59-62, solve the inequalities. (See...Ch. 2.6 - For Exercises 59-62, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - Prob. 75PECh. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - For Exercises 63-84, solve the inequalities. (See...Ch. 2.6 - A professional fireworks team shoots an 8-in....Ch. 2.6 - Suppose that a basketball player jumps straight up...Ch. 2.6 - For a certain stretch of road, the distance d (in...Ch. 2.6 - The population Pt of a bacteria culture is given...Ch. 2.6 - Prob. 89PECh. 2.6 - The average round trip speed 5inmph of a vehicle...Ch. 2.6 - A rectangular quit is to be made so that the...Ch. 2.6 - A landscaping team plans to build a rectangular...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - For Exercises 93-102, write the domain of the...Ch. 2.6 - Let a,b,andc represent positive real numbers,...Ch. 2.6 - Let a,b,andc represent positive real numbers,...Ch. 2.6 - Explain how the solution set to the inequality fx0...Ch. 2.6 - Prob. 106PECh. 2.6 - Explain why x2+2x2+10 has no solution.Ch. 2.6 - Prob. 108PECh. 2.6 - Prob. 109PECh. 2.6 - Prob. 110PECh. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - Prob. 115PECh. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - Prob. 118PECh. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - The procedure to solve a polynomial or rational...Ch. 2.6 - Prob. 121PECh. 2.6 - Given the inequality,...Ch. 2.6 - An engineer for a food manufacturer designs an...Ch. 2.6 - The concentration Ct (in ng/mL) of a drug in the...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - Prob. 4PRECh. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - Prob. 23PRECh. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.6 - For Exercises 1-30, solve the equations and...Ch. 2.7 - Write a variation model using k as the constant of...Ch. 2.7 - Write a variable model using k as the constant of...Ch. 2.7 - The amount of the medicine ampicillin that a...Ch. 2.7 - The yield on a bond varies inversely as the price....Ch. 2.7 - The amount of simple interest earned in an account...Ch. 2.7 - If k is a nonzero constant real number, then the...Ch. 2.7 - If k is a nonzero constant real number, then the...Ch. 2.7 - The value of k in the variation models y=kxandy=kx...Ch. 2.7 - If y varies directly as two or more other...Ch. 2.7 - a. Given y=2x, evaluate y for the given values of...Ch. 2.7 - Prob. 6PECh. 2.7 - The time required to drive from Atlanta, Georgia,...Ch. 2.7 - The amount of a person’s paycheck varies as the...Ch. 2.7 - The volume of a right circular cone varies as the...Ch. 2.7 - A student’s grade on a test varies as the...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 11-20, write a variation model using...Ch. 2.7 - For Exercises 21-26, find the constant of...Ch. 2.7 - For Exercises 21-26, find the constant of...Ch. 2.7 - For Exercises 21-26, find the constant of...Ch. 2.7 - For Exercises 21-26, find the constant of...Ch. 2.7 - For Exercises 21-26, find the constant of...Ch. 2.7 - For Exercises 21-26, find the constant of...Ch. 2.7 - The value of y equal 4 when x=10. Find y when x=5...Ch. 2.7 - The value of y equal 24 when x is 12. Find y when...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 29-48, use a variation model to...Ch. 2.7 - For Exercises 49-52, use the given data to find a...Ch. 2.7 - For Exercises 49-52, use the given data to find a...Ch. 2.7 - For Exercises 49-52, use the given data to find a...Ch. 2.7 - For Exercises 49-52, use the given data to find a...Ch. 2.7 - Which formula(s) can represent a variation model?...Ch. 2.7 - Which formula(s) can represent a variation model?...Ch. 2.7 - For Exercises 55-56, write a statement in words...Ch. 2.7 - For Exercises 55-56, write a statement in words...Ch. 2.7 - The light from a lightbulb radiates outward in all...Ch. 2.7 - Kepler's third law states that the square of the...Ch. 2.7 - The intensity of radiation varies inversely as the...Ch. 2.7 - Suppose that y varies inversely as the cube of x....Ch. 2.7 - Suppose that y varies directly as x2 and inversely...Ch. 2.7 - Suppose that y varies directly as x5 and inversely...Ch. 2.7 - Suppose that y varies jointly as x and w3. . If x...Ch. 2.7 - Suppose that y varies jointly as x4 and w. If x is...Ch. 2 - Given fx=x+52+2, identity the vertex of the graph...Ch. 2 - For Exercises 2-3, a. Write the equation in vertex...Ch. 2 - For Exercises 2-3, a. Write the equation in vertex...Ch. 2 - a. Use the vertex formula to determine the vertex...Ch. 2 - Suppose that a farmer encloses a corral for cattle...Ch. 2 - Suppose that p is the probability that a randomly...Ch. 2 - The annual expenditure for cell phones and...Ch. 2 - For Exercises 8-11, a. Determine the end behaviour...Ch. 2 - For Exercises 8-11, a. Determine the end behaviour...Ch. 2 - For Exercises 8-11, a. Determine the end behaviour...Ch. 2 - Prob. 11RECh. 2 - Determine whether the intermediate value theorem...Ch. 2 - For Exercises 13-16, determine if the statement is...Ch. 2 - For Exercises 13-16, determine if the statement is...Ch. 2 - For Exercises 13-16, determine if the statement is...Ch. 2 - For Exercises 13-16, determine if the statement is...Ch. 2 - For Exercises 17-18, a. Divide the polynomials. b....Ch. 2 - For Exercises 17-18, a. Divide the polynomials. b....Ch. 2 - For Exercises 19-20, use synthetic division to...Ch. 2 - For Exercises 19-20, use synthetic division to...Ch. 2 - Prob. 21RECh. 2 - For Exercises 21-22, use the remainder theorem to...Ch. 2 - For Exercises 23-24, use the remainder theorem to...Ch. 2 - For Exercises 23-24, use the remainder theorem to...Ch. 2 - For Exercises 25-26, use the factor theorem to...Ch. 2 - For Exercises 25-26, use the factor theorem to...Ch. 2 - Factor fx=15x367x2+26x+8, given that 23 is a zero...Ch. 2 - Write a third-degree polynomial fx with zeros...Ch. 2 - Write a third-degree polynomial fx with integer...Ch. 2 - Given fx=2x57x4+9x318x2+4x+40, a. How many zeros...Ch. 2 - Given fx=x4+4x3+2x28x8, a. How many zeros does fx...Ch. 2 - Prob. 32RECh. 2 - Given fx=x422x3+119x2+66x366 and that 11i is a...Ch. 2 - Write a polynomial fx of lowest degree with real...Ch. 2 - Write a third-degree polynomial fx with integer...Ch. 2 - For Exercises 36-37, determine the number of...Ch. 2 - For Exercises 36-37, determine the number of...Ch. 2 - For Exercises 38-39. a. Determine if the upper...Ch. 2 - For Exercises 38-39. a. Determine if the upper...Ch. 2 - Refer to the graph of y=fx and complete the...Ch. 2 - For Exercises 41-42, determine the vertical...Ch. 2 - For Exercises 41-42, determine the vertical...Ch. 2 - Prob. 43RECh. 2 - For Exercises 43-45, a. Determine the horizontal...Ch. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - For Exercises 48-51, graph the function....Ch. 2 - For Exercises 48-51, graph the function....Ch. 2 - For Exercises 48-51, graph the function. qx=12x2+6Ch. 2 - After taking a certain class, the percentage of...Ch. 2 - Prob. 53RECh. 2 - The graph of y=fx is given. Solve the...Ch. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - For Exercises 57-66, solve the inequalities. tt318Ch. 2 - For Exercises 57-66, solve the inequalities....Ch. 2 - Prob. 59RECh. 2 - For Exercises 57-66, solve the inequalities....Ch. 2 - For Exercises 57-66, solve the inequalities....Ch. 2 - Prob. 62RECh. 2 - For Exercises 57-66, solve the inequalities....Ch. 2 - Prob. 64RECh. 2 - For Exercises 57-66, solve the inequalities. 3x22xCh. 2 - Prob. 66RECh. 2 - A sports trainer has monthly costs of $80 for...Ch. 2 - A Child throws a ball straight upwards to his...Ch. 2 - For Exercises 69-71, write a variation model using...Ch. 2 - For Exercises 69-71, write a variation model using...Ch. 2 - For Exercises 69-71, write a variation model using...Ch. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - The weight of a ball varies directly as the cube...Ch. 2 - Prob. 75RECh. 2 - The power in an electric circuit varies jointly as...Ch. 2 - Coulomb's law states that the force F of...Ch. 2 - Given fx=2x212x+16, a. Write the equation in...Ch. 2 - Prob. 2TCh. 2 - Prob. 3TCh. 2 - Prob. 4TCh. 2 - Determine whether the intermediate value theorem...Ch. 2 - a. Divide the polynomials. 2x44x3+x5x23x+1 b....Ch. 2 - Given fx=5x4+47x3+80x251x9,...Ch. 2 - Prob. 8TCh. 2 - Given fx=3x4+7x312x214x+12, a. How many zeros does...Ch. 2 - Write a third-degree polynomial fx with integer...Ch. 2 - Determine the number of possible positive and...Ch. 2 - For Exercises 12-14, determine the asymptotes...Ch. 2 - For Exercises 12-14, determine the asymptotes...Ch. 2 - For Exercises 12-14, determine the asymptotes...Ch. 2 - For Exercise 15-17, graph the function. mx=1x2+3Ch. 2 - For Exercise 15-17, graph the function. hx=4x24Ch. 2 - For Exercise 15-17, graph the function. kx=x22x+1xCh. 2 - For Exercises 18-24, solve the inequality. c2c+20Ch. 2 - For Exercises 18-24, solve the inequality. y313y12Ch. 2 - For Exercises 18-24, solve the inequality....Ch. 2 - Prob. 21TCh. 2 - Prob. 22TCh. 2 - For Exercises 18-24, solve the inequality. 4x290Ch. 2 - Prob. 24TCh. 2 - write a variation model using k as the constant of...Ch. 2 - Prob. 26TCh. 2 - The surface area of a cube varies directly as the...Ch. 2 - Prob. 28TCh. 2 - The pressure of wind on a wall varies jointly as...Ch. 2 - The population Pt of rabbits in a wildlife area t...Ch. 2 - Prob. 31TCh. 2 - Suppose that a rocket is shot straight upward from...Ch. 2 - The number of yearly visits to physicians’...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
The dimensions of the rectangle.
Pre-Algebra Student Edition
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
Snow Depth (Example 3) Eric wants to go skiing tomorrow, but only if there are 3 inches or more of new snow. Ac...
Introductory Statistics
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Other techniques Evaluate the following limits, where a and b are fixed real numbers. 41. limx4x2164x
Calculus: Early Transcendentals (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 9. Use fundamental theorem of calculus to find the derivative d a) *dt sin(x) b)(x)√1-2 dtarrow_forward3. Evaluate the definite integral: a) √66x²+8dx b) x dx c) f*(2e* - 2)dx d) √√9-x² e) (2-5x)dx f) cos(x)dx 8)²₁₂√4-x2 h) f7dx i) f² 6xdx j) ²₂(4x+3)dxarrow_forward2. Consider the integral √(2x+1)dx (a) Find the Riemann sum for this integral using right endpoints and n-4. (b) Find the Riemann sum for this same integral, using left endpoints and n=4arrow_forward
- Problem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forwardX Solve numerically: = 0,95 In xarrow_forwardX Solve numerically: = 0,95 In xarrow_forward
- Please as many detarrow_forward8–23. Sketching vector fields Sketch the following vector fieldsarrow_forward25-30. Normal and tangential components For the vector field F and curve C, complete the following: a. Determine the points (if any) along the curve C at which the vector field F is tangent to C. b. Determine the points (if any) along the curve C at which the vector field F is normal to C. c. Sketch C and a few representative vectors of F on C. 25. F = (2½³, 0); c = {(x, y); y − x² = 1} 26. F = x (23 - 212) ; C = {(x, y); y = x² = 1}) , 2 27. F(x, y); C = {(x, y): x² + y² = 4} 28. F = (y, x); C = {(x, y): x² + y² = 1} 29. F = (x, y); C = 30. F = (y, x); C = {(x, y): x = 1} {(x, y): x² + y² = 1}arrow_forward
- ٣/١ B msl kd 180 Ka, Sin (1) I sin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 G 5005 1000 s = 1000-950 Copper bosses 5kW Rotor input 5 0.05 : loo kw 6) 1 /0001 ined sove in peaper I need a detailed solution on paper please وه اذا ميريد شرح الكتب فقط ١٥٠ DC 7) rotor a ' (y+xlny + xe*)dx + (xsiny + xlnx + dy = 0. Q1// Find the solution of: ( 357arrow_forward۳/۱ R₂ = X2 2) slots per pole per phase 3/31 B. 180 msl Kas Sin (I) 1sin() sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30): 0.866 4) Rotating 5) Synchronous speeds 120×50 looo G 1000-950 1000 Copper losses 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 Find the general solution of the following equations: QI//y(4)-16y= 0. Find the general solution of the following equations: Q2ll yll-4y/ +13y=esinx.arrow_forwardR₂ = X2 2) slots per pole per phase = 3/31 B-180 60 msl kd Kas Sin () 2 I sin (6) sin(30) Sin (30) اذا مريد شرح الكتب بس 0 بالفراغ 3 Cos (30) 0.866 4) Rotating ined sove in peaper 5) Synchronous speed s 120×50 6 s = 1000-950 1000 Copper losses 5kw Rotor input 5 0.05 6) 1 loo kw اذا ميريد شرح الكتب فقط Look 7) rotov DC I need a detailed solution on paper please 0 64 Solve the following equations: 0 Q1// Find the solution of: ( y • with y(0) = 1. dx x²+y²arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Interpreting Graphs of Quadratic Equations (GMAT/GRE/CAT/Bank PO/SSC CGL) | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=BHgewRcuoRM;License: Standard YouTube License, CC-BY
Solve a Trig Equation in Quadratic Form Using the Quadratic Formula (Cosine, 4 Solutions); Author: Mathispower4u;https://www.youtube.com/watch?v=N6jw_i74AVQ;License: Standard YouTube License, CC-BY