
Concept explainers
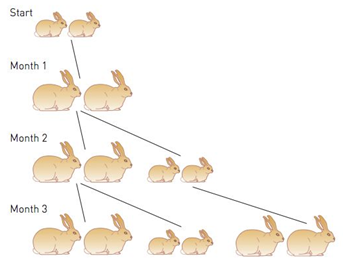
Baby bunnies. This question gave the Fibonacci sequence its name. It was posed and answered by Leonardo of Pisa, better known as Fibonacci.
Suppose we have a pair of baby rabbits: one male and one female. Let us assume that rabbits cannot reproduce until they are one month old and that they have a one-month gestation period. Once they start reproducing, they produce a pair of bunnies each month (one of each sex). Assuming that no pair ever dies, how many pairs of rabbits will exist in a particular month?
During the first month, the bunnies grow into rabbits. After two months, they are the proud parents of a pair of bunnies. There will now be two pairs of rabbits: the original, mature pair and a new pair of bunnies. The next month, the original pair produces another pair of bunnies, but the new pair of bunnies is unable to reproduce until the following month. Thus we have:

Continue to fill in this chart and search for a pattern. Here is a suggestion: Draw a family tree to keep track of the offspring.
We’ll use the symbol F1 to stand for the first Fibonacci number, F2 for the second Fibonacci number, F3, for the third Fibonacci number, and so forth. So
So, the rule for generating the next Fibonacci number by adding up the previous two can now be stated symbolically, in general, as:
Want to see the full answer?
Check out a sample textbook solution
Chapter 2 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking 4e + WileyPLUS Registration Card
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics (13th Edition)
Thinking Mathematically (6th Edition)
Precalculus
College Algebra (7th Edition)
Pre-Algebra Student Edition
- Matlab. Add the awnsers for the * questions in the code comments.arrow_forward4. Suppose f A → B is a bijection. Prove that f-1: BA is a bijection.arrow_forwardProve by mathematical induction that for any positive integer n, the sum of the cubes of the first n natural numbers is given by: n Σκ k=1 (n(n + 1))²arrow_forward
- 1 L'Ina (ln x) 2020 dx 0arrow_forwardCalibri BIUAAAA ויו Text in Italian is not being checked. Do you want to add it as a proofing language? Task 12 Fig 1 75 75 75 Fig 2 Fig 3j Add Figures 1 to 3 each shows a top view and a front view of models. Make use of the lineated paper for isometric projection and take each block on the paper as being 10mm x 10mm. Use the indicated sizes and draw an isometric view of each of the three models Samsung Galaxy A04earrow_forwarda) show that the empty set and sigletonset are convex set. 6) show that every sub space of linear space X is convex but the convers heed not be true. c) let Mand N be two convex set of a linear Space X and KEF Show that MUN is conevex and (ii) M-N is convex or hot A and is MSN or NSM show that MUN convex or not, 385arrow_forward
- xp x+xarrow_forwardFor the given graph, determine the following. -3 12 УА 4 3 - -1 ° 1 2 3 x -1. -2- a. Determine for which values of a the lim f (x) exists but f is not continuous at x = a. a b. Determine for which values of a the function is continuous but not differentiable at x = a. aarrow_forwardI write with prove one-to-one linear Sanction but not onto Lexample.) b) write with Prove on to linear function but not oh-to-on (example). c) write with prove example x=y St Xandy two linear space over Sielad F.arrow_forward
- Use the following graph of ƒ (x) to evaluate ƒ' (−1) and ƒ' (2). y +10+ 9 8 7 6 5 4 3 2 1- -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 x 3 4 0 8 9 10 -2 3 -4 5 -6 -7 -8 -9 -10- f'(-1)= f' (2)arrow_forwardFor the following function f and real number a, a. find the slope of the tangent line mtan = = f' (a), and b. find the equation of the tangent line to f at x = a. f(x) = 2 = ;a=2 a. Slope: b. Equation of tangent line: yarrow_forwardFor the following function f and real number a, a. find the slope of the tangent line mtan = f' (a), and b. find the equation of the tangent line to f at x = a. f(x) = 2x² + 3x; a = 2 a. Slope: b. Equation of tangent line: yarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell  College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



