
CALCULUS,VOLUME 1 (OER)
17th Edition
ISBN: 2810022307715
Author: OpenStax
Publisher: XANEDU C
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 2.2, Problem 64E
In the following exercises, use the graph of function
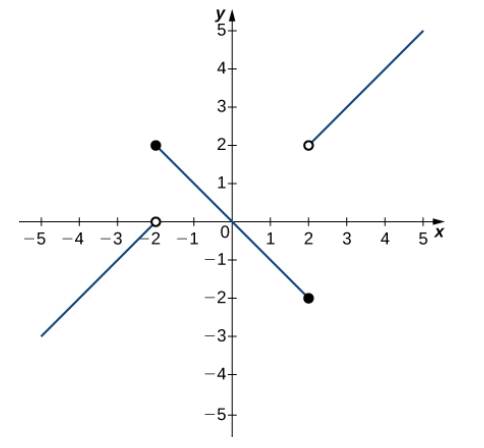
64.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find three horizontal tangents between [0,10]
Not use ai please
No chatgpt pls will upvote
Chapter 2 Solutions
CALCULUS,VOLUME 1 (OER)
Ch. 2.1 - For the following exercises, points P(l, 2) and...Ch. 2.1 - For the following exercises, points P(l, 2) and...Ch. 2.1 - For the following exercises, points P(l, 2) and...Ch. 2.1 - For the following exercises, points P(l, 1) and...Ch. 2.1 - For the following exercises, points P(l, 1) and...Ch. 2.1 - For the following exercises, points P(l, 1) and...Ch. 2.1 - For the following exercises, points P(4, 2) and...Ch. 2.1 - For the following exercises, points P(4, 2) and...Ch. 2.1 - For the following exercises, points P(4, 2) and...Ch. 2.1 - For the following exercises, points P(l.5, 0) and...
Ch. 2.1 - For the following exercises, points P( 1.5, 0) and...Ch. 2.1 - For the following exercises, points P( 1.5, 0) and...Ch. 2.1 - For the following exercises, points P(-1, -1) and...Ch. 2.1 - For the following exercises, points P(-1,-1) and...Ch. 2.1 - For the following exercises, points P(-1, - 1) and...Ch. 2.1 - For the following exercises, the position function...Ch. 2.1 - For the following exercises, the position function...Ch. 2.1 - For the following exercises, consider a stone...Ch. 2.1 - For the following exercises, consider a stone...Ch. 2.1 - For the following exercises, consider a rocket...Ch. 2.1 - For the following exercises, consider a rocket...Ch. 2.1 - For the following exercises, consider an athlete...Ch. 2.1 - For the following exercises, consider an athlete...Ch. 2.1 - For the following exercises, consider the...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.1 - For the following exercises, consider the...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.1 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - For the following exercises, consider the function...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - [T] In the following exercises, set up a table of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, consider the graph of...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the following...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, use the graph of the...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - In the following exercises, sketch the graph of a...Ch. 2.2 - Shock waves arise in many physical applications,...Ch. 2.2 - A track coach uses a camera with a fast shutter to...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - Some of the geometric formulas we take for granted...Ch. 2.3 - In the following exercises, use the limit Laws to...Ch. 2.3 - In the following exercises, use the limit laws to...Ch. 2.3 - In the following exercises, use the limit laws to...Ch. 2.3 - In the following exercises, use the limit laws to...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - ]In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, use direct...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - In the following exercises, assume that...Ch. 2.3 - [T] In the following exercises, use a calculator...Ch. 2.3 - [T] In the following exercises, use a calculator...Ch. 2.3 - [T] In the following exercises, use a calculator...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - yIn the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - In the following exercises, use the following...Ch. 2.3 - For the following problems, evaluate the limit...Ch. 2.3 - For the following problems, evaluate the limit...Ch. 2.3 - For the following problems, evaluate the limit...Ch. 2.3 - [T] In physics, the magnitude of an electric field...Ch. 2.3 - [T] The density of an object is given by its mass...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, determine the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - For the following exercises, decide if the...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, find the value(s) of k...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - In the following exercises, use the Intermediate...Ch. 2.4 - Consider the graph of the function y=f(x) shown in...Ch. 2.4 - Let f(x)={3x,x1x3,x1 . Sketch the graph of f. Is...Ch. 2.4 - Let f(x)=x41x21forx1,1 . a. Sketch the graph of f....Ch. 2.4 - Sketch the graph of the function y=f(x) with...Ch. 2.4 - Sketch the graph of the function y=f(x) with...Ch. 2.4 - In the following exercises, suppose y=f(x) is...Ch. 2.4 - In the following exercises, suppose y=f(x) is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - Determine whether each of the given statements is...Ch. 2.4 - [T] The following problems consider the scalar...Ch. 2.4 - [T] The following problems consider the scalar...Ch. 2.4 - [T] The following problems consider the scalar...Ch. 2.4 - [T] After a certain distance D has passed, the...Ch. 2.4 - As the rocket travels away from Earth’s surface,...Ch. 2.4 - wqProve the following functions are continuous...Ch. 2.4 - Prove the following functions are continuous...Ch. 2.4 - Prove the following functions are continuous...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - In the following exercises, write the appropriate ...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - The following graph of the function f satisfies...Ch. 2.5 - [T] In the following exercises, use a graphing...Ch. 2.5 - [T] In the following exercises, use a graphing...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - In the following exercises, use the precise...Ch. 2.5 - An engineer is using a machine to cut a flat...Ch. 2.5 - Use the precise definition of limit to prove that...Ch. 2.5 - Using precise definitions of limits, prove that...Ch. 2.5 - Using precise definitions of limits, prove that...Ch. 2.5 - Using precise definitions of limits, prove that...Ch. 2.5 - Using the function from the previous exercise, use...Ch. 2.5 - limxa(f(x)g(x))=LMCh. 2.5 - limxa[cf(x)]=cL for any real constant c (Hint....Ch. 2.5 - ...Ch. 2 - wTrue or False. In the following exercises,...Ch. 2 - True or False. In the following exercises, justify...Ch. 2 - True or False. In the following exercises, justify...Ch. 2 - True or False. In the following exercises, justify...Ch. 2 - Using the graph, find each limit or explain why...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - wIn the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, evaluate the limit...Ch. 2 - In the following exercises, use the squeeze...Ch. 2 - In the following exercises, use the squeeze...Ch. 2 - In the following exercises, use the squeeze...Ch. 2 - In the following exercises, determine the value of...Ch. 2 - In the following exercises, determine the value of...Ch. 2 - In the following exercises, use the precise...Ch. 2 - In the following exercises, use the precise...Ch. 2 - A ball is thrown into the air and the vertical...Ch. 2 - A particle moving along a line has a displacement...Ch. 2 - From the previous exercises, estimate the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
29-36. Total and Annual Returns. Compute the total and annual returns on the following investments.
29. Five ye...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
In Exercises 9-22, change the Cartesian integral into an equivalent polar integral. Then evaluate the polar int...
University Calculus: Early Transcendentals (4th Edition)
Calculating derivatives Find dy/dx for the following functions. 27. y = cos2 x
Calculus: Early Transcendentals (2nd Edition)
Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forwardnot use ai pleasearrow_forward4 In the integral dxf1dy (7)², make the change of variables x = ½(r− s), y = ½(r + s), and evaluate the integral. Hint: Find the limits on r and s by sketching the area of integration in the (x, y) plane along with the r and s axes, and then show that the same area can be covered by s from 0 to r and r from 0 to 1.arrow_forward
- 7. What are all values of 0, for 0≤0<2л, where 2 sin² 0=-sin? - 5π 6 π (A) 0, л, and 6 7π (B) 0,л, 11π , and 6 6 π 3π π (C) 5π 2 2 3 , and π 3π 2π (D) 2' 2'3 , and 3 4元 3 1 די } I -2m 3 1 -3 บ 1 # 1 I 3# 3m 8. The graph of g is shown above. Which of the following is an expression for g(x)? (A) 1+ tan(x) (B) 1-tan (x) (C) 1-tan (2x) (D) 1-tan + X - 9. The function j is given by j(x)=2(sin x)(cos x)-cos x. Solve j(x) = 0 for values of x in the interval Quiz A: Topic 3.10 Trigonometric Equations and Inequalities Created by Bryan Passwaterarrow_forwardnot use ai pleasearrow_forward-xx0. B2 If Xfx(x) find the MGF in the case that fx(x) = - 1 28 exp{-|x − a\/ẞ}, Use the MGF to compute E(X) and Var(X).arrow_forward
- Name Assume there is the following simplified grade book: Homework Labs | Final Exam | Project Avery 95 98 90 100 Blake 90 96 Carlos 83 79 Dax 55 30 228 92 95 79 90 65 60 Assume that the weights used to compute the final grades are homework 0.3, labs 0.2, the final 0.35, and the project 0.15. | Write an explicit formula to compute Avery's final grade using a single inner product. Write an explicit formula to compute everyone's final grade simultane- ously using a single matrix-vector product.arrow_forward1. Explicitly compute by hand (with work shown) the following Frobenius inner products 00 4.56 3.12 (a) ((º º º). (156 (b) 10.9 -1 0 2)), Fro 5')) Froarrow_forward3. Let 4 0 0 00 0 0 1.2 0 00 0 0 0 -10.1 0 0 0 D = 0 0 0 00 0 0 0 0 05 0 0 0 0 0 0 2.8 Either explicitly compute D-¹ or explain why it doesn't exist.arrow_forward
- 4. [9 points] Assume that B, C, E are all 3 x 3 matrices such that BC == -64 -1 0 3 4 4 4 -2 2 CB=-1-2 4 BE -2 1 3 EC = 1 3 2 -7, 1 6 -6 2-5 -7 -2 Explicitly compute the following by hand. (I.e., write out the entries of the 3 × 3 matrix.) (a) [3 points] B(E+C) (b) [3 points] (E+B)C (c) [3 points] ETBTarrow_forward6. Consider the matrices G = 0 (3) -3\ -3 2 and H = -1 2 0 5 0 5 5 noting that H(:, 3) = 2H(:,1) + H(:, 2). Is G invertible? Explain your answer. Is H invertible? Explain your answer. Use co-factor expansion to find the determinant of H. (Hint: expand the 2nd or 3rd row)arrow_forwardB3 Consider X ~ Bern(p) (a) Find Mx(t), the moment generating function of X. iid (b) If X1,..., Xn Bern(p), find the MGF, say My (t) of n Y = ΣΧ (c) Using the fact that i=1 n lim (1 (1+2)"= N→X = e² find limn→∞ My (t) in the case that p satisfies limn→∞ np = λ, say. (d) State the distribution of Y in the case that n is not large, and the distribution of Y in the limiting case described in the question.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you

Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY