Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
4th Edition
ISBN: 9780134686974
Author: Michael Sullivan, Michael Sullivan III
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.2, Problem 19AYU
Video Games and Grade-Point Average Professor Grant Alexander wanted to find a linear model that relates the number of hours a student plays video games each week. , to the cumulative grade-point average. , of the student. He obtained a random sample of 10 full-time students at his college and asked each student to disclose the number of hours spent playing video games and the student’s cumulative grade-point average.
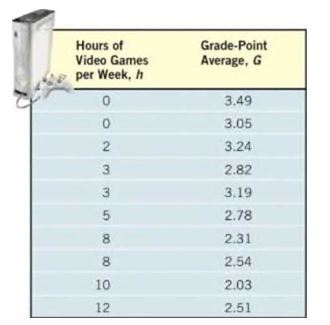
(a) Explain why the number of hours spent playing video games is the independent variable and cumulative grade-point average is the dependent variable.
(b) Use a graphing utility to draw a
(c) Use a graphing utility to find the line of best fit that models the relation between number of hours of video game playing each week and grade-point average. Express the model using function notation.
(d) Interpret the slope.
(e) Predict the grade-point average of a student who plays video games for 8 hours each week.
(f) How many hours of video game playing do you think a student plays whose grade-point average is ?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Rylee's car is stuck in the mud. Roman and Shanice come along in a truck to help pull her out. They attach
one end of a tow strap to the front of the car and the other end to the truck's trailer hitch, and the truck
starts to pull. Meanwhile, Roman and Shanice get behind the car and push. The truck generates a
horizontal force of 377 lb on the car. Roman and Shanice are pushing at a slight upward angle and generate
a force of 119 lb on the car. These forces can be represented by vectors, as shown in the figure below. The
angle between these vectors is 20.2°. Find the resultant force (the vector sum), then give its magnitude
and its direction angle from the positive x-axis.
119 lb
20.2°
377 lb
An airplane flies due west at an airspeed of 428 mph. The wind blows in the direction of 41° south of west
at 50 mph. What is the ground speed of the airplane? What is the bearing of the airplane?
A vector with magnitude 5 points in a direction 190 degrees counterclockwise from the positive x axis.
Write the vector in component form, and show your answers accurate to 3 decimal places.
Chapter 2 Solutions
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
Ch. 2.1 - Graph y=2x3.(pp.22-27)Ch. 2.1 - Find the slope of the line joining the points (...Ch. 2.1 - Find the average rate of change of f(x)=3x22, from...Ch. 2.1 - Solve: 6x900=15x+2850 . (pp. A44-A46)Ch. 2.1 - If f(x)=x24, find f(2). (pp. 47-49)Ch. 2.1 - 6. True or False the graph of the function is...Ch. 2.1 - For the graph of the linear function f( x )=mx+b ,...Ch. 2.1 - If the slope m of the graph of a linear function...Ch. 2.1 - 9. True or False The slope of a nonvertical line...Ch. 2.1 - True or False The average rate of change of f( x...
Ch. 2.1 - 11. What is the only type of function that has a...Ch. 2.1 - A car has 12,500 miles on its odometer. Say the...Ch. 2.1 - In Problems 13-20, a linear function is...Ch. 2.1 - In Problems 13-20, a linear function is given. a....Ch. 2.1 - In Problems 13-20, a linear function is given. a....Ch. 2.1 - In Problems 13-20, a linear function is given. a....Ch. 2.1 - In Problems 13-20, a linear function is...Ch. 2.1 - In Problems 13-20, a linear function is...Ch. 2.1 - In Problems 13-20, a linear function is given. a....Ch. 2.1 - In Problems 13-20, a linear function is...Ch. 2.1 - In Problem 21-26,
21.
(a) Find the zero of each...Ch. 2.1 - In Problem 21-26
22.
(a) Find the zero of each...Ch. 2.1 - In problem 21-26, f(x)=5x+10 Find the zero of each...Ch. 2.1 - In problem 21-26,
24.
(a) Find the zero of each...Ch. 2.1 - In problem 21-26,
25.
(a) Find the zero of each...Ch. 2.1 - In problem 21-26, G(x)=13x4 Find the zero of each...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - In Problems 21-28, determine whether the given...Ch. 2.1 - Suppose that f( x )=4x1 and g(x)=2x+5 . a. Solve...Ch. 2.1 - Suppose that f( x )=3x+5 and g(x)=2x+15 . a. Solve...Ch. 2.1 - In parts (a) - (f), use the following figure. a....Ch. 2.1 - In parts (a) - (f), use the following figure. a....Ch. 2.1 - 33. In parts (a) and (b), use the following...Ch. 2.1 - In parts (a) and (b), use the following figure. a....Ch. 2.1 - In parts (a) and (b), use the following figure. a....Ch. 2.1 - In parts (a) and (b), use the following figure. a....Ch. 2.1 - 43. Getting Towed The cost C, in dollars, for...Ch. 2.1 - Phone Charges Themonthlycost C, in dollars, for...Ch. 2.1 - Supply and Demand Suppose that the quantity...Ch. 2.1 - 40. Supply and Demand Suppose that the quantity...Ch. 2.1 - Taxes The function T(x)=0.15(x9325)+932.50...Ch. 2.1 - Competitive Balance Tax In 2011, major league...Ch. 2.1 - The point at which a companys profits equal zero...Ch. 2.1 - The point at which a companys profits equal zero...Ch. 2.1 - 45. Straight-line Depreciation Suppose that a...Ch. 2.1 - Straight-line Depreciation Suppose that a company...Ch. 2.1 - 47. Cost Function The simplest cost function is...Ch. 2.1 - Cost function Refer to problem 49. Suppose that...Ch. 2.1 - 55. Truck Rentals A truck rental company rents a...Ch. 2.1 - International Data Plan A mobile phone company...Ch. 2.1 - Developing a Linear Model from Data The following...Ch. 2.1 - Developing a Linear Model from Data The following...Ch. 2.1 - Which of the following functions might have the...Ch. 2.1 - Which of the following functions might have the...Ch. 2.1 - 55. Under what circumstances is a linear function...Ch. 2.1 - Explain how the graph of f( x )=mx+b can be used...Ch. 2.1 - Problems 57-60 are based on material teamed...Ch. 2.1 - Problems 57-60 are based on material teamed...Ch. 2.1 - Problems 57-60 are based on material teamed...Ch. 2.1 - Problems 57-60 are based on material teamed...Ch. 2.2 - 1. Plot the points (1, 5), (2, 6), (3, 9), (1, 12)...Ch. 2.2 - 2. Find an equation of the line containing the...Ch. 2.2 - A _____________ is used to help us to see what...Ch. 2.2 - Prob. 4AYUCh. 2.2 - In Problems 5-10, examine the scatter diagram and...Ch. 2.2 - In Problems 5-10, examine the scatter diagram and...Ch. 2.2 - In Problems 5-10, examine the scatter diagram and...Ch. 2.2 - In Problems 5-10, examine the scatter diagram and...Ch. 2.2 - In Problems 5-10, examine the scatter diagram and...Ch. 2.2 - In Problems 5-10, examine the scatter diagram and...Ch. 2.2 - In Problems 11 16, Draw a scatter diagram. Select...Ch. 2.2 - In Problems 11 – 16,
Draw a scatter...Ch. 2.2 - In Problems 11 16, Draw a scatter diagram. Select...Ch. 2.2 - In Problems 11 16, Draw a scatter diagram. Select...Ch. 2.2 - In Problems 11 – 16,
Draw a scatter...Ch. 2.2 - In Problems 11 – 16,
Draw a scatter...Ch. 2.2 - Candy The following data represent the weight (in...Ch. 2.2 - Tornadoes The following data represent the width...Ch. 2.2 - Video Games and Grade-Point Average Professor...Ch. 2.2 - Hurricanes The following data represent the...Ch. 2.2 - Homeruns A baseball analyst wishes to find a...Ch. 2.2 - Maternal Age versus Down Syndrome A biologist...Ch. 2.2 - U.S. Advertising The following data represent the...Ch. 2.2 - 24. Find the line of best fit for the ordered...Ch. 2.2 - 25. What does a correlation coefficient of 0...Ch. 2.2 - Explain why it does not make sense to interpret...Ch. 2.2 - 27. Refer to Problem 19. Solve G(h)= 0. Provide...Ch. 2.2 - 28. Find an equation for the line containing the...Ch. 2.2 - 29. Find the domain of f(x) = .
Ch. 2.2 - For f(x)=5x8 and g(x)= x 2 3x+4 , find (gf)(x) .Ch. 2.2 - Write the function whose graph is the graph of y=...Ch. 2.3 - 1. (a) Factor: (pp. A36 – A37)
(b) Factor ...Ch. 2.3 - 2. Simplify: (pp. A58 – A59)
Ch. 2.3 - 3. Solve: (p. A4)
Ch. 2.3 - 4. To complete the square of ______ (add/subtract)...Ch. 2.3 - 5. If what point is on the graph of f? (pp. 60...Ch. 2.3 - Is 3 a zero of f(x)=x2+4x+3?(pp. 61 62)Ch. 2.3 - 7. When a quadratic equation has a repeated...Ch. 2.3 - The quantity b24ac is called the _________ of a...Ch. 2.3 - How many real zeros can a quadratic function have?Ch. 2.3 - State the quadratic formula.Ch. 2.3 - True or False If the discriminant of a quadratic...Ch. 2.3 - A quadratic equation is sometimes called a...Ch. 2.3 - In Problems 13 26, find the zeros of each...Ch. 2.3 - In Problems 13-26, find the zeros of each...Ch. 2.3 - In Problems 13-26, find the zeros of each...Ch. 2.3 - In Problems 13-26, find the zeros of each...Ch. 2.3 - In Problems 13-26, find the zeros of each...Ch. 2.3 - Prob. 18AYUCh. 2.3 - Prob. 19AYUCh. 2.3 - Prob. 20AYUCh. 2.3 - Prob. 21AYUCh. 2.3 - Prob. 22AYUCh. 2.3 - Prob. 23AYUCh. 2.3 - Prob. 24AYUCh. 2.3 - In Problems 13-26, find the zeros of each...Ch. 2.3 - Prob. 26AYUCh. 2.3 - Prob. 27AYUCh. 2.3 - Prob. 28AYUCh. 2.3 - In problem 27-32, find the zeros of each quadratic...Ch. 2.3 - Prob. 30AYUCh. 2.3 - Prob. 31AYUCh. 2.3 - Prob. 32AYUCh. 2.3 - In problem 33-38, find the zeros of each quadratic...Ch. 2.3 - Prob. 34AYUCh. 2.3 - Prob. 35AYUCh. 2.3 - Prob. 36AYUCh. 2.3 - In problem 33-38, find the zeros of each quadratic...Ch. 2.3 - Prob. 38AYUCh. 2.3 - Prob. 39AYUCh. 2.3 - Prob. 40AYUCh. 2.3 - Prob. 41AYUCh. 2.3 - Prob. 42AYUCh. 2.3 - Prob. 43AYUCh. 2.3 - Prob. 44AYUCh. 2.3 - Prob. 45AYUCh. 2.3 - Prob. 46AYUCh. 2.3 - Prob. 47AYUCh. 2.3 - Prob. 48AYUCh. 2.3 - In problems 3952, find the real zeroes, if any of...Ch. 2.3 - Prob. 50AYUCh. 2.3 - Prob. 51AYUCh. 2.3 - Prob. 52AYUCh. 2.3 - In problems 5358, solve f(x)=g(x). What are the...Ch. 2.3 - Prob. 54AYUCh. 2.3 - Prob. 55AYUCh. 2.3 - Prob. 56AYUCh. 2.3 - Prob. 57AYUCh. 2.3 - Prob. 58AYUCh. 2.3 - Prob. 59AYUCh. 2.3 - Prob. 60AYUCh. 2.3 - Prob. 61AYUCh. 2.3 - Prob. 62AYUCh. 2.3 - Prob. 63AYUCh. 2.3 - Prob. 64AYUCh. 2.3 - Prob. 65AYUCh. 2.3 - Prob. 66AYUCh. 2.3 - Prob. 67AYUCh. 2.3 - Prob. 68AYUCh. 2.3 - Prob. 69AYUCh. 2.3 - Prob. 70AYUCh. 2.3 - Prob. 71AYUCh. 2.3 - Prob. 72AYUCh. 2.3 - In problems 59-76, find the real zeros of each...Ch. 2.3 - Prob. 74AYUCh. 2.3 - Prob. 75AYUCh. 2.3 - Prob. 76AYUCh. 2.3 - Prob. 77AYUCh. 2.3 - Prob. 78AYUCh. 2.3 - Prob. 79AYUCh. 2.3 - Prob. 80AYUCh. 2.3 - Prob. 81AYUCh. 2.3 - Prob. 82AYUCh. 2.3 - Prob. 83AYUCh. 2.3 - Prob. 84AYUCh. 2.3 - Prob. 85AYUCh. 2.3 - Prob. 86AYUCh. 2.3 - Prob. 87AYUCh. 2.3 - Prob. 88AYUCh. 2.3 - Prob. 89AYUCh. 2.3 - Prob. 90AYUCh. 2.3 - In problem 89-94,
Graph each function using...Ch. 2.3 - In problem 89-94, Graph each function using...Ch. 2.3 - In problem 89-94, Graph each function using...Ch. 2.3 - In problem 89-94, Graph each function using...Ch. 2.3 - In problems 95-100, solve . What are the points of...Ch. 2.3 - In problems 95-100, solve . What are the points of...Ch. 2.3 - In problems 95-100, solve . What are the points of...Ch. 2.3 - In problems 95-100, solve f(x)=g(x). What are the...Ch. 2.3 - In problems 95-100, solve . What are the points of...Ch. 2.3 - In problems 95-100, solve . What are the points of...Ch. 2.3 - Suppose that f(x)=x2+5x14 and g(x)=x+3x4 Find the...Ch. 2.3 - 102. Suppose that, and
(a) Find the zeros of...Ch. 2.3 - Dimensions of a window, The function A(x)=x(x+2)...Ch. 2.3 - Dimensions of a window, The function A(x)=x(x+1)...Ch. 2.3 - Constructing a Box, An open box is to be...Ch. 2.3 - Constructing a Box Rework Problem 105 if the box...Ch. 2.3 - Physics A ball is thrown vertically upward from...Ch. 2.3 - 108. Physics An object is propelled vertically...Ch. 2.3 - Consecutive Integers The sum S of the consecutive...Ch. 2.3 - Geometry The number of diagonals D of a polygon...Ch. 2.3 - Show that the sum of the roots of a quadratic...Ch. 2.3 - Show that the product of the roots of quadratic...Ch. 2.3 - Find k such that the function f(x)=kx2+x+k=0 has a...Ch. 2.3 - 114. Find k such that the function has a repeated...Ch. 2.3 - Show that the real zeros of the function...Ch. 2.3 - Show that real zeros of the function f(x)=ax2+bx+c...Ch. 2.3 - 117. Which of the following pairs of equations are...Ch. 2.3 - 118. Describe four methods you might use to find...Ch. 2.3 - 119. Explain the benefits of evaluating the...Ch. 2.3 - Create three quadratic functions, one having two...Ch. 2.3 - The word quadratic seems to imply four (quad), yet...Ch. 2.3 - 122. How many times can the graphs of two...Ch. 2.3 - Problems are based on material learned earlier in...Ch. 2.3 - Problem 123-126 are based on material learned...Ch. 2.3 - Problem 123-126 are based on material learned...Ch. 2.3 - Problems are based on material learned earlier in...Ch. 2.4 - 1. List the intercepts of the equation y = x2 - 9....Ch. 2.4 - Prob. 2AYUCh. 2.4 - To complete the square of x 2 5x , you add the...Ch. 2.4 - 4. To graph y = (x - 4)2 you shift the graph of y...Ch. 2.4 - 5. The graph of a quadratic function is called...Ch. 2.4 - 6. The vertical line passing through the vertex of...Ch. 2.4 - The x-coordinate of the vertex of f( x )=a x 2...Ch. 2.4 - True for False The graph of f(x)=2x2+3x4 opens up.Ch. 2.4 - True or False The y-coordinate of the vertex of f(...Ch. 2.4 - 10. True or False If the discriminant b2- 4ac = 0,...Ch. 2.4 - 11. If b2 - 4ac > 0, which of the following...Ch. 2.4 - 12. If the graph of f(x) = ax2 + bx + c, a ≠ 0,...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 13-20, match each graph to one the...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In Problems 21-32, graph the function f by...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems , (a) graph each quadratic function by...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In problems 3348, (a) graph each quadratic...Ch. 2.4 - In Problems 49-54, determine the quadratic...Ch. 2.4 - In Problems 49-54, determine the quadratic...Ch. 2.4 - In Problems 49-54, determine the quadratic...Ch. 2.4 - In Problems 49-54, determine the quadratic...Ch. 2.4 - In Problems 49-54, determine the quadratic...Ch. 2.4 - In Problems 49-54, determine the quadratic...Ch. 2.4 - In Problems 55 – 62, determine, without graphing,...Ch. 2.4 - In Problems 55-62, determine, without graphing,...Ch. 2.4 - In Problems 55-62, determine, without graphing,...Ch. 2.4 - In Problems 55-62, determine, without graphing,...Ch. 2.4 - In Problems 55 62, determine, without graphing,...Ch. 2.4 - In Problems 55-62, determine, without graphing,...Ch. 2.4 - In Problems 55 62, determine, without graphing,...Ch. 2.4 - In Problems 55-62, determine, without graphing,...Ch. 2.4 - In Problems 63-74, (a) graph each function, (b)...Ch. 2.4 - In Problems 63-74, (a) graph each function, (b)...Ch. 2.4 - 65. In problem (a) graph each quadratic function,...Ch. 2.4 - 66. In problem (a) graph each quadratic, (b)...Ch. 2.4 - Prob. 67AYUCh. 2.4 - 68. In problem (a) graph each function, (b)...Ch. 2.4 - In Problems 63-74, (a) graph each function, (b)...Ch. 2.4 - 70. In problem (a) graph each function, (b)...Ch. 2.4 - 71. In problem (a) graph each function (b)...Ch. 2.4 - In Problems 63-74, (a) graph each function, (b)...Ch. 2.4 - In Problems 63 74, (a) graph each function, (b)...Ch. 2.4 - In Problems 63 74, (a) graph each function, (b)...Ch. 2.4 - 75. The graph of the function f(x) = ax2 + bx + c...Ch. 2.4 - The graph of the function f(x)=a x 2 +bx+c has...Ch. 2.4 - In Problems 77-82, for the given functions fandg ,...Ch. 2.4 - In Problems 77-82, for the given functions f and...Ch. 2.4 - In Problems 77-82, for the given functions fandg ,...Ch. 2.4 - In Problems 77-82, for the given functions f and...Ch. 2.4 - In Problems 77-82, for the given functions fandg ,...Ch. 2.4 - In Problems 77-82, for the given functions fandg ,...Ch. 2.4 - Answer Problems 83 and 84 using the following: A...Ch. 2.4 - Answer Problems 83 and 84 using the following: A...Ch. 2.4 - 85. Suppose that f(x) = x2 + 4x - 21.
What is the...Ch. 2.4 - 86. Suppose that f(x) = x2 + 2x - 8.
(a) What is...Ch. 2.4 - Find the point on the line that is closest to the...Ch. 2.4 - Find the point on the line y=x+1 that is closes to...Ch. 2.4 - 89. Maximizing Revenue Suppose that the...Ch. 2.4 - 90. Maximizing Revenue The John Deere company has...Ch. 2.4 - Minimizing Marginal Cost The marginal cost of a...Ch. 2.4 - 92. Minimizing Marginal Cost (See Problem 91.) The...Ch. 2.4 - Business The monthly revenue R achieved by selling...Ch. 2.4 - Business The daily revenue R achieved by selling x...Ch. 2.4 - Stopping Distance An accepted relationship between...Ch. 2.4 - Birthrate for Unmarried Women In the United...Ch. 2.4 - 97. Let f(x) = ax2 + bx + c, where a, b, and c are...Ch. 2.4 - Make up a quadratic function that opens down and...Ch. 2.4 - 99. On one set of coordinate axes, graph the...Ch. 2.4 - 100. On one set of coordinate axes, graph the...Ch. 2.4 - State the circumstances that cause the graph of a...Ch. 2.4 - 102. Why does the graph of a quadratic function...Ch. 2.4 - Can a quadratic function have a range of ( , ) ?...Ch. 2.4 - 104. What are the possibilities for the number of...Ch. 2.4 - Determine whether x 2 +4 y 2 =16 is symmetric...Ch. 2.4 - Find the domain of .
Ch. 2.4 - Prob. 107AYUCh. 2.4 - Write the function whose graph is the graph of y=...Ch. 2.5 - Solve the inequality 3x27 .Ch. 2.5 - 2. Write using inequality notation and graph the...Ch. 2.5 -
3.
(a)
(b)...Ch. 2.5 - (a) g( x )0 (b) g( x )0Ch. 2.5 - 5.
(a)
(b)
Ch. 2.5 - (a) f( x )g( x ) (b) f( x )g( x )Ch. 2.5 - x 2 3x100Ch. 2.5 - x 2 +3x100Ch. 2.5 - 9.
Ch. 2.5 - 10.
Ch. 2.5 - x 2 90Ch. 2.5 - 12.
Ch. 2.5 - 13.
Ch. 2.5 - 14.
Ch. 2.5 - 2 x 2 5x+3Ch. 2.5 - 16.
Ch. 2.5 - x 2 x+10Ch. 2.5 - x 2 +2x+40Ch. 2.5 - 19.
Ch. 2.5 - 20.
Ch. 2.5 - 21.
Ch. 2.5 - 2( 2 x 2 3x )9Ch. 2.5 - What is the domain of the function f( x )= x 2 16...Ch. 2.5 - 24. What is the domain of the function ?
Ch. 2.5 - In Problems 25-32, use the given functions f and g...Ch. 2.5 - In Problems 25-32, use the given functions f and...Ch. 2.5 - In Problems 25-32, use the given functions f and...Ch. 2.5 - In Problems 25-32, use the given functions f and...Ch. 2.5 - In Problems 25-32, use the given functions f and...Ch. 2.5 - In Problems 25-32, use the given functions f and g...Ch. 2.5 - In Problems 25-32, use the given functions f and g...Ch. 2.5 - In Problems 25-32, use the given functions f and...Ch. 2.5 - Physics A ball is thrown vertically upward with an...Ch. 2.5 - 34. Physics A ball is thrown vertically upward...Ch. 2.5 - 35. Revenue Suppose that the manufacturer of a gas...Ch. 2.5 - Revenue The John Deere company has found that the...Ch. 2.5 - Artillery A projectile Fired from the point ( 0,0...Ch. 2.5 - 38. Runaway Car Using Hooke's Law, we can show...Ch. 2.5 - Show that the inequality ( x4 ) 2 0 has exactly...Ch. 2.5 - 40. Show that the inequality has one real number...Ch. 2.5 - 41. Explain why the inequality has all real...Ch. 2.5 - 42. Explain why the inequality has the empty set...Ch. 2.5 - 43. Explain the circumstances under which the...Ch. 2.5 - Determine the domain of f( x )= 102x .Ch. 2.5 - Determine algebraically whether f( x )= x x 2 +9...Ch. 2.5 - Consider the linear function f( x )= 2 3 x6 . (a)...Ch. 2.5 - Determine whether the graphs of 6x3y=10 and 2x+y=8...Ch. 2.6 - Translate the following sentence into a...Ch. 2.6 - Use a graphing utility to find the line of best...Ch. 2.6 - Maximizing Revenue, The price p (in dollars) and...Ch. 2.6 - Maximizing Revenue, The price p (in dollars) and...Ch. 2.6 - Maximizing Revenue, The price p (in dollars) and...Ch. 2.6 - 6. Maximizing Revenue, The price (in dollars)...Ch. 2.6 - 7. Enclosing a Rectangular Field David has 400...Ch. 2.6 - 8. Enclosing a Rectangular Field Beth has 3000...Ch. 2.6 - Enclosing a Rectangular Field with a Fence A...Ch. 2.6 - Enclosing a Rectangular Field with a Fence A...Ch. 2.6 - A projectile is fired from a cliff 200 feet above...Ch. 2.6 - 12. Analyzing the motion of a projectile a...Ch. 2.6 - 13. Suspension Bridge A suspension bridge with...Ch. 2.6 - Architecture A parabolic arch has a span of 120...Ch. 2.6 - 15. Constructing Rain Gutters A rain gutter is to...Ch. 2.6 - 16. Norman Windows A Norman window has the shape...Ch. 2.6 - 17. Constructing a Stadium A track-and-field...Ch. 2.6 - Architecture A special window has the shape of a...Ch. 2.6 - 19. Chemical Reactions A self-catalytic chemical...Ch. 2.6 - 20. Calculus: Simpson's Rule The figure shows the...Ch. 2.6 - 21. Use the result obtained in Problem 20 to find...Ch. 2.6 - Use the result obtained in Problem 20 to find the...Ch. 2.6 - Use the result obtained in Problem 20 to find the...Ch. 2.6 - Use the result obtained in Problem 20 to find the...Ch. 2.6 - Life Cycle Hypothesis Household income varies with...Ch. 2.6 - 26. Height of a Rail A shot-putter throws a hall...Ch. 2.6 - Which Model? The following data represent the...Ch. 2.6 - 28. Which Model? An engineer collect the...Ch. 2.6 - Which Model? The following data represent the...Ch. 2.6 - Which Model? A cricket makes a chirping noise by...Ch. 2.6 - Find an equation of the line containing the points...Ch. 2.6 - 31. Refer to Example 1 in this section. Notice...Ch. 2.6 - 33. Find the distance between the points P1 = (4,...Ch. 2.6 - Prob. 34AYUCh. 2.6 - Problems 3235 are based material learned earlier...Ch. 2.7 - Name the integers and the rational numbers in the...Ch. 2.7 - True or False Rational numbers and irrational...Ch. 2.7 - (2+i)(34i) ________ (pp. A92 A97)Ch. 2.7 - 4. The conjugate of is________
Ch. 2.7 - Prob. 5AYUCh. 2.7 - 6. = _________. (pp. A92 – A97)
Ch. 2.7 - If 23i is a zero of a quadratic function with real...Ch. 2.7 - 8. True or False Consider the quadratic function ...Ch. 2.7 - In Problems 9 – 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - Prob. 16AYUCh. 2.7 - In Problems 9 – 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 – 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - Prob. 21AYUCh. 2.7 - Prob. 22AYUCh. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - In Problems 9 24, find the complex zeros of each...Ch. 2.7 - Prob. 25AYUCh. 2.7 - Prob. 26AYUCh. 2.7 - Prob. 27AYUCh. 2.7 - Prob. 28AYUCh. 2.7 - Prob. 29AYUCh. 2.7 - Prob. 30AYUCh. 2.7 - In Problems 31 – 34, find all complex zeros of...Ch. 2.7 - In Problems 31 – 34, find all complex zeros of...Ch. 2.7 - In Problems 31 – 34, find all complex zeros of...Ch. 2.7 - Prob. 34AYUCh. 2.7 - Prob. 35AYUCh. 2.7 - Prob. 36AYUCh. 2.7 - Prob. 37AYUCh. 2.7 - Prob. 38AYUCh. 2.8 - 1. Graph the inequality. (pp.A4-A5)
Ch. 2.8 - Prob. 2AYUCh. 2.8 - Prob. 3AYUCh. 2.8 - Prob. 4AYUCh. 2.8 - Prob. 5AYUCh. 2.8 - Prob. 6AYUCh. 2.8 - Prob. 7AYUCh. 2.8 - Prob. 8AYUCh. 2.8 - |u|a will have no solution if a _____________0.Ch. 2.8 - Prob. 10AYUCh. 2.8 - Prob. 11AYUCh. 2.8 - Prob. 12AYUCh. 2.8 - Prob. 13AYUCh. 2.8 - Prob. 14AYUCh. 2.8 - In problems 13 – 16, use the graphs of the...Ch. 2.8 - Prob. 16AYUCh. 2.8 - In problems 17 38, solve each equation. |x|=6Ch. 2.8 - In problems 17 – 38, solve each equation.
18.
Ch. 2.8 - In problems 17 – 38, solve each equation.
19.
Ch. 2.8 - In problems 17 – 38, solve each equation.
20.
Ch. 2.8 - In problems 17 38, solve each equation....Ch. 2.8 - In problems 17 38, solve each equation. |12z|+6=9Ch. 2.8 - In problems 17 – 38, solve each equation.
23.
Ch. 2.8 - In problems 17 – 38, solve each equation.
24.
Ch. 2.8 - Prob. 25AYUCh. 2.8 - In problems 17 – 38, solve each equation.
26.
Ch. 2.8 - Prob. 27AYUCh. 2.8 - Prob. 28AYUCh. 2.8 - Prob. 29AYUCh. 2.8 - Prob. 30AYUCh. 2.8 - Prob. 31AYUCh. 2.8 - Prob. 32AYUCh. 2.8 - Prob. 33AYUCh. 2.8 - Prob. 34AYUCh. 2.8 - Prob. 35AYUCh. 2.8 - Prob. 36AYUCh. 2.8 - In problems 17 38, solve each equation. |x2+x1|=1Ch. 2.8 - Prob. 38AYUCh. 2.8 - In problems 39-62, solve each absolute value...Ch. 2.8 - Prob. 40AYUCh. 2.8 - Prob. 41AYUCh. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - Prob. 44AYUCh. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - Prob. 46AYUCh. 2.8 - Prob. 47AYUCh. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - Prob. 49AYUCh. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - Prob. 52AYUCh. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - Prob. 54AYUCh. 2.8 - Prob. 55AYUCh. 2.8 - Prob. 56AYUCh. 2.8 - Prob. 57AYUCh. 2.8 - Prob. 58AYUCh. 2.8 - In problem 39-62, solve each absolute value...Ch. 2.8 - Prob. 60AYUCh. 2.8 - Prob. 61AYUCh. 2.8 - Prob. 62AYUCh. 2.8 - Prob. 63AYUCh. 2.8 - Prob. 64AYUCh. 2.8 - If f(x)=|3x+2| and g(x)=x+10 solve. f(x)=g(x)...Ch. 2.8 - Prob. 66AYUCh. 2.8 - Prob. 67AYUCh. 2.8 - Prob. 68AYUCh. 2.8 - Prob. 69AYUCh. 2.8 - Prob. 70AYUCh. 2.8 - 71. Tolerance, A certain rod in an internal...Ch. 2.8 - Tolerance, A certain rod in an internal combustion...Ch. 2.8 - 73. IQ Scores, According to the Stanford- binet IQ...Ch. 2.8 - 74. Gestation Period The length of human...Ch. 2.8 - Prob. 75AYUCh. 2.8 - Prob. 76AYUCh. 2.8 - Prob. 77AYUCh. 2.8 - Prob. 78AYUCh. 2.8 - Prob. 79AYUCh. 2.8 - Prob. 80AYUCh. 2.8 - Prob. 81AYUCh. 2 - In Problem 1-3:
Determine the slope and...Ch. 2 - In Problem 1-3:
Determine the slope and...Ch. 2 - In Problem 1-3: Determine the slope and...Ch. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - In Problem 7-12. Find the zeros of each quadratic...Ch. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - In Problems 913, (a) graph each quadratic function...Ch. 2 - Prob. 24RECh. 2 - In Problems 913, (a) graph each quadratic function...Ch. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - In Problems 1416, determine whether the given...Ch. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - In Problems 19 and 20, find the quadratic function...Ch. 2 - Prob. 31RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - 22. Sales Commissions Bill has just been offered a...Ch. 2 - Demand Equation The price p(in dollars) and the...Ch. 2 - Geometry The diagonal of a rectangle measures 10...Ch. 2 -
25. Minimizing Marginal Cost Callaway Golf...Ch. 2 - Landscaping A landscape engineer has 200 feet of...Ch. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Bone Length Research performed at NASA, led by Dr....Ch. 2 - Advertising A small manufacturing firm collected...Ch. 2 - Prob. 1CTCh. 2 - Prob. 2CTCh. 2 - In Problems 2 and 3, find the intercepts, if any,...Ch. 2 - In Problems 2 and 3, find the intercepts, if any,...Ch. 2 - Prob. 7CTCh. 2 - Prob. 5CTCh. 2 - Prob. 6CTCh. 2 - Prob. 8CTCh. 2 - Prob. 9CTCh. 2 - Prob. 10CTCh. 2 - Prob. 11CTCh. 2 - Prob. 12CTCh. 2 - Prob. 13CTCh. 2 - Prob. 14CTCh. 2 - Prob. 15CTCh. 2 - Prob. 16CTCh. 2 - Prob. 17CTCh. 2 - Prob. 18CTCh. 2 - 19. Consider these two data sets:
Set A...Ch. 2 - Prob. 1CRCh. 2 - Prob. 2CRCh. 2 - Prob. 3CRCh. 2 - Prob. 4CRCh. 2 - Prob. 5CRCh. 2 - Prob. 6CRCh. 2 - Prob. 7CRCh. 2 - Prob. 8CRCh. 2 - Prob. 9CRCh. 2 - Prob. 10CRCh. 2 - Prob. 11CRCh. 2 - Prob. 12CRCh. 2 - Prob. 13CRCh. 2 - Prob. 14CRCh. 2 - Prob. 15CR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- ||A||=23 45° Find the EXACT components of the vector above using the angle shown.arrow_forwardGiven ƒ = (10, -10) and q = (-8, −7), find ||ƒ— q|| and dƒ-9. Give EXACT answers. You do NOT have to simplify your radicals!arrow_forwardFind a vector (u) with magnitude 7 in the direction of v = (2,4) Give EXACT answer. You do NOT have to simplify your radicals!arrow_forward
- Given g = (-5, 10) and u = (5, 2), find -4ğ - 6.arrow_forwardGiven the vector v→=⟨3,-5⟩, find the magnitude and angle in which the vector points (measured in radians counterclockwise from the positive x-axis and 0≤θ<2π). Round each decimal number to two places.arrow_forwardplease include radicals in answerarrow_forward
- 3 4/3 3213 + 8 for 1 ≤x≤8. Find the length of the curve y=xarrow_forwardGiven that the outward flux of a vector field through the sphere of radius r centered at the origin is 5(1 cos(2r)) sin(r), and D is the value of the divergence of the vector field at the origin, the value of sin (2D) is -0.998 0.616 0.963 0.486 0.835 -0.070 -0.668 -0.129arrow_forward10 The hypotenuse of a right triangle has one end at the origin and one end on the curve y = Express the area of the triangle as a function of x. A(x) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License