
a.
To determine: The futures price for contract maturity dates on February 14, 2016; May 21 2016 and November 18, 2016 assuming that the interest rate is 3% per year, stock index- 2,000, dividend yield of 2.0%.
Introduction:
Spot-futures parity relationship: It shows the relationship between the futures price andthe spot price. Sometimes, there is a difference between the futures price andthe spot price. It may be due to changes in interest rates, expiry time and dividends paid. So, this difference has to be equated. The mathematical equation which balances the underlying price and its future price may be termed as spot-future parity.
a.
Answer to Problem 17PS
The future prices as on maturity date is as follows:
| Current date January 1, 2016 | 2000.00 |
| February 14, 2016 | 2002.40 |
| May 21, 2016 | 2022.93 |
| November 18,2016 | 2051.71 |
Explanation of Solution
Current date= January 1, 2016
Interest rate per year = 3%
Stock index pay dividend of 2% at 2000
Dividend yield=2%
From the given information, let us calculate the future price.
The formula to be used here is:
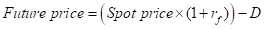
Where,
Spot price= Price of the stock in cash market;
rf= Risk -free rate of interest;
D=Dividend paid by the company.
We should be aware of the fact that T-Bill or treasury bills and Government securities carry risk-free interest rate.
Since the future price expires in a short time, the above formula needs to be modified. The modified formula is as follows:

Where,
x= number of expiry days;
Spot price= Price of the stock in cash market;
rf= Risk -free rate of interest;
D=Dividend paid by the company.
So, let us now calculate the future prices:-
i) When the maturity date is February 14,2016
The risk-free interest rate is given for the whole year. Since we are given three different periods, we have to calculate number of days in each case.
In this case, Number of days= January 1,2016 to February 14, 2016

So now, we have to calculate the risk-free interest rate for 45 days.
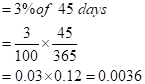
In the same way, even the dividend date of 2% is given for the entire year.
So, the dividend earned for 45 days would be
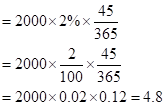
So, let us now substitute the value in the given formula:

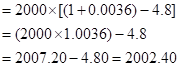
Hence the
ii) When the maturity date is May 21,2016
In this case, Number of days= January 1,2016 to May 21, 2016
=January+February+March+April+21 days of May= 141 days
So now, we have to calculate the risk-free interest rate for 141 days.
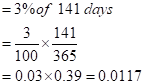
In the same way, even the dividend date of 2% is given for the entire year.
So, the dividend earned for 141 days would be
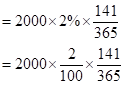
So, let us now substitute the value in the given formula:
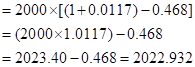
Hence the future value is 2022.932 when the maturity date is May 21, 2016.
iii) When the maturity date is November 18, 2016.
In this case, Number of days= January 1,2016 to May 21, 2016
=January+February+March+April+May+June+July+August+September+October+18 days of November= 322 days
So now, we have to calculate the risk-free interest rate for 322 days.
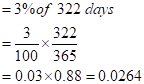
In the same way, even the dividend date of 2% is given for the entire year.
So, the dividend earned for 322 days would be
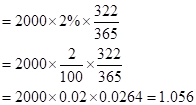
So, let us now substitute the value in the given formula:
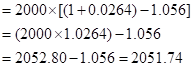
Hence the future value is 2051.74 when the maturity date is November 18, 2016.
b.
To determine: The term structure of future prices if the dividend yield is higher than the risk-free rate.
Introduction:
Dividend yield: It is supposed to be the amount of money paid by the company to its shareholders. Normally, dividend yield is calculated for one year of investment and is represented in terms of percentages.
b.
Answer to Problem 17PS
The future prices as on maturity date is as follows:
| February 14, 2016 | 1997.60 |
| May 21, 2016 | 2007.80 |
| November 18,2016 | 1982.40 |
Explanation of Solution
Current date= January 1, 2016
Interest rate per year = 3%
Stock index pay dividend of 2% at 2000
Dividend yield=2%
Let us consider the dividend yield to be 4%.
Let us now calculate the term structure of future prices if the dividend yield is 4%.
iv) When the maturity date is February 14,2016
The risk-free interest rate is given for the whole year. Since we are given three different periods, we have to calculate number of days in each case.
So now, we have to calculate the risk-free interest rate for 45 days.
From the above calculation now we are aware that number of days in this case =45 days and the risk-free interest rate for 45 days is 0.0036
The dividend date of 4% is given for the entire year.
So, the dividend earned for 45 days would be
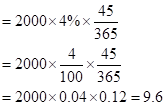
So, let us now substitute the value in the given formula:
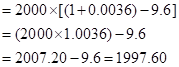
Hence the future value is 1997.60 when the maturity date is February 14, 2016.
v) When the maturity date is May 21,2016
In this case, the number of days is 141 days and the risk-free interest rate for 141 days is 0.0117.
In the same way, even the dividend date of 4% is given for the entire year.
So, the dividend earned for 141 days would be
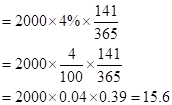
So, let us now substitute the value in the given formula:

Hence the future value is 2007.80 when the maturity date is May 21, 2016.
vi) When the maturity date is November 18, 2016.
In this case, the number of days is 322 days and the risk-free interest rate for 322 days is 0.0264.
In the same way, even the dividend date of 4% is given for the entire year.
So, the dividend earned for 322 days would be
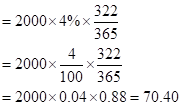
So, let us now substitute the value in the given formula:

Hence the future value is 1982.40 when the maturity date is November 18, 2016.
We can conclude that an increase in dividend yield is showing a decrease in the future prices.
Want to see more full solutions like this?
- PLEASE ANSWER THE COLUMN FULLY AND CORRECTLY PLEASE DO THE RIGHT CALCULATION DOUBLE CHECK AS WELL TO GIVE ME THE RIGHT ANSWER REQUIRED: Given the following information, what are the NZD/SGD currency against currency bid-ask quotations? Note: Do not round intermediate calculations. Round your answers to 4 decimal places. Bank Quotations American Terms European Terms Bid Ask Bid Ask New Zealand dollar 0.733 0.7340 1.3870 1.3884 Singapore dollar 0.6186 0.6191 1.6423 1.6436 answer Bid Ask New Zealand dollar ? ? Singapore dollar ? ?arrow_forwardAbout this Assignment For the Corporate Finance 301 assignment, you will submit a research paper that analyzes and discusses organizational financial risks. You will apply knowledge acquired in the course and use the concepts of multiple financial risks as the basis of research and analysis. The research paper should follow APA formatting style. Audience: upper-level business students. Project Prompt Write a 1,000-1,200-word analysis discussing financial risk concepts and assess the impact of the different financial risks on an organization. For this assignment, you will structure your assignment using four research paper sections associated with corporate risk management, as studied in the course. Base your research paper on the financial statements analyzed in Corporate Finance 301 assignment 2 and apply the knowledge acquired in the analysis. Define each financial risk, discuss the risk associated components, and evaluate the financial risks and how they affect the corporation's…arrow_forwardBobby Nelson, made deposits of $880 at the end of each year for 6 years. Interest is 6% compounded annually. What is the value of Bobby’s annuity at the end of 6 years?arrow_forward
- 1. Find the future value if $1,250 is invested in Simple interest account paying 6.5%: a. for 5 years b. for 20 years 2. Find the future amount $ 35,000 is invested for 30 years at 4.25% compounded: a. annually b. Quarterly c. monthly d. weekly 3. How much should be put into an account today that pays 7.75% compounded monthly if you need $10,000 in 5 years. 4. Find the effective rate for: a. 5.75% compounded quarterly b. 6.25% compounded daily. 5. $50 is invested at the end of each month into an account paying 7.5% compounded monthly. How much will be in the account after 5 years?…arrow_forwardSolve step by step no aiarrow_forwardDont use ai solve itarrow_forward
