
A computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = .22, P(A2) = .25, P(A3) = .28, P(A1 ∩ A2) = .11, P(A1 ∩ A3) = .05, P(A2 ∩ A3) = .07, P(A1 ∩ A2 ∩ A3) = .01. Express in words each of the following events, and compute the
- a. A1 ∪ A2
- b. A1′∩ A2′ [Hint: (A1 ∪ A2)′ = A′1 ∩ A′2]
- c. A1 ∪ A2 ∪ A3
- d. A′1 ∩ A′2 ∩ A′3
- e. A′1 ∩ A′2 ∩ A3
- f. (A′1 ∩ A′2 ) ∪ A3
a.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Given info:
The data represents the projects of the consulting firm.
Here, A1 be awarded project 1,
A2 be awarded project 2,
A3 be awarded project .
Let
Calculation:
Addition rule:
For any two events A and B,
Complement:
The complement of the event A contains the set of all element that are contained in sample space S and not contained in event A. it is denoted as
Union:
The union of two events A1 or A2 contains set of all elements which are either in A1, A2, or both the events. It is denoted by
Intersection:
The intersection of two event A1 and A2 contains set all of element which are in both A1 and A2. It is denoted by
The probability of A1 or A2 can be obtained as
Thus, the probability of an event
b.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The probability of
The event
Thus, the probability of an event
c.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
Addition rule:
For any three events A, B and C ,
The event
The probability of
Thus, the probability of an event
d.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The event
The probability of
Thus, the probability of an event
e.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The event
The event
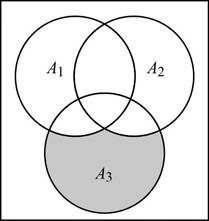
From the Venn diagram, the probability of
Thus, the probability of an event
f.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The event
The event
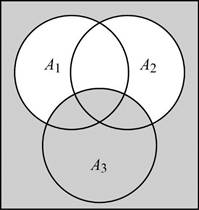
The probability of
Thus, the probability of an event
Want to see more full solutions like this?
Chapter 2 Solutions
Probability and Statistics for Engineering and the Sciences
- Consider an MA(6) model with θ1 = 0.5, θ2 = −25, θ3 = 0.125, θ4 = −0.0625, θ5 = 0.03125, and θ6 = −0.015625. Find a much simpler model that has nearly the same ψ-weights.arrow_forwardLet {Yt} be an AR(2) process of the special form Yt = φ2Yt − 2 + et. Use first principles to find the range of values of φ2 for which the process is stationary.arrow_forwardDescribe the important characteristics of the autocorrelation function for the following models: (a) MA(1), (b) MA(2), (c) AR(1), (d) AR(2), and (e) ARMA(1,1).arrow_forward
- « CENGAGE MINDTAP Quiz: Chapter 38 Assignment: Quiz: Chapter 38 ips Questions ra1kw08h_ch38.15m 13. 14. 15. O Which sentence has modifiers in the correct place? O a. When called, she for a medical emergency responds quickly. b. Without giving away too much of the plot, Helena described the heroine's actions in the film. O c. Nearly the snakebite victim died before the proper antitoxin was injected. . O O 16 16. O 17. 18. O 19. O 20 20. 21 21. 22. 22 DS 23. 23 24. 25. O O Oarrow_forwardQuestions ra1kw08h_ch36.14m 12. 13. 14. 15. 16. Ӧ 17. 18. 19. OS 20. Two separate sentences need Oa. two separate subjects. Ob. two dependent clauses. c. one shared subject.arrow_forwardCustomers experiencing technical difficulty with their Internet cable service may call an 800 number for technical support. It takes the technician between 30 seconds and 11 minutes to resolve the problem. The distribution of this support time follows the uniform distribution. Required: a. What are the values for a and b in minutes? Note: Do not round your intermediate calculations. Round your answers to 1 decimal place. b-1. What is the mean time to resolve the problem? b-2. What is the standard deviation of the time? c. What percent of the problems take more than 5 minutes to resolve? d. Suppose we wish to find the middle 50% of the problem-solving times. What are the end points of these two times?arrow_forward
- Exercise 6-6 (Algo) (LO6-3) The director of admissions at Kinzua University in Nova Scotia estimated the distribution of student admissions for the fall semester on the basis of past experience. Admissions Probability 1,100 0.5 1,400 0.4 1,300 0.1 Click here for the Excel Data File Required: What is the expected number of admissions for the fall semester? Compute the variance and the standard deviation of the number of admissions. Note: Round your standard deviation to 2 decimal places.arrow_forward1. Find the mean of the x-values (x-bar) and the mean of the y-values (y-bar) and write/label each here: 2. Label the second row in the table using proper notation; then, complete the table. In the fifth and sixth columns, show the 'products' of what you're multiplying, as well as the answers. X y x minus x-bar y minus y-bar (x minus x-bar)(y minus y-bar) (x minus x-bar)^2 xy 16 20 34 4-2 5 2 3. Write the sums that represents Sxx and Sxy in the table, at the bottom of their respective columns. 4. Find the slope of the Regression line: bi = (simplify your answer) 5. Find the y-intercept of the Regression line, and then write the equation of the Regression line. Show your work. Then, BOX your final answer. Express your line as "y-hat equals...arrow_forwardApply STATA commands & submit the output for each question only when indicated below i. Generate the log of birthweight and family income of children. Name these new variables Ibwght & Ifaminc. Include the output of this code. ii. Apply the command sum with the detail option to the variable faminc. Note: you should find the 25th percentile value, the 50th percentile and the 75th percentile value of faminc from the output - you will need it to answer the next question Include the output of this code. iii. iv. Use the output from part ii of this question to Generate a variable called "high_faminc" that takes a value 1 if faminc is less than or equal to the 25th percentile, it takes the value 2 if faminc is greater than 25th percentile but less than or equal to the 50th percentile, it takes the value 3 if faminc is greater than 50th percentile but less than or equal to the 75th percentile, it takes the value 4 if faminc is greater than the 75th percentile. Include the outcome of this code…arrow_forward
- solve this on paperarrow_forwardApply STATA commands & submit the output for each question only when indicated below i. Apply the command egen to create a variable called "wyd" which is the rowtotal function on variables bwght & faminc. ii. Apply the list command for the first 10 observations to show that the code in part i worked. Include the outcome of this code iii. Apply the egen command to create a new variable called "bwghtsum" using the sum function on variable bwght by the variable high_faminc (Note: need to apply the bysort' statement) iv. Apply the "by high_faminc" statement to find the V. descriptive statistics of bwght and bwghtsum Include the output of this code. Why is there a difference between the standard deviations of bwght and bwghtsum from part iv of this question?arrow_forwardAccording to a health information website, the distribution of adults’ diastolic blood pressure (in millimeters of mercury, mmHg) can be modeled by a normal distribution with mean 70 mmHg and standard deviation 20 mmHg. b. Above what diastolic pressure would classify someone in the highest 1% of blood pressures? Show all calculations used.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

