Essential Calculus: Early Transcendentals; MAC 2311 Sequence| MAC 2281Sequence USF (Essential Calculus)
2nd Edition
ISBN: 9781285101552
Author: James Stewart
Publisher: Cenage
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.2, Problem 12E
Shown is the graph of the population function P(t) for yeast cells in a laboratory culture. Use method of Example 1 to graph the derivative P'(t) What does the graph of P' tell us about the yeast population?
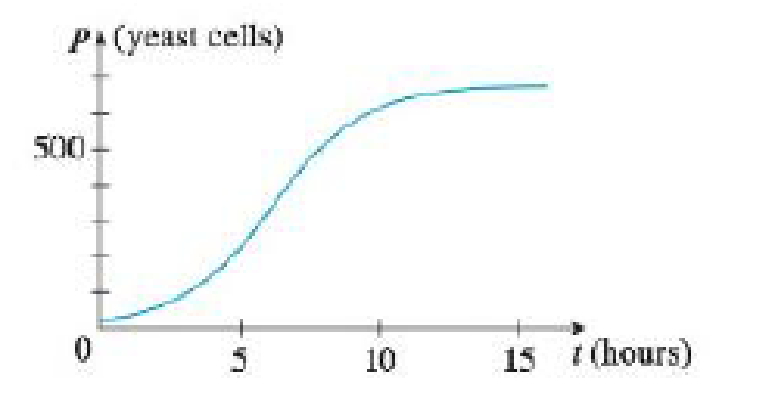
Example 1
FIGURE 1
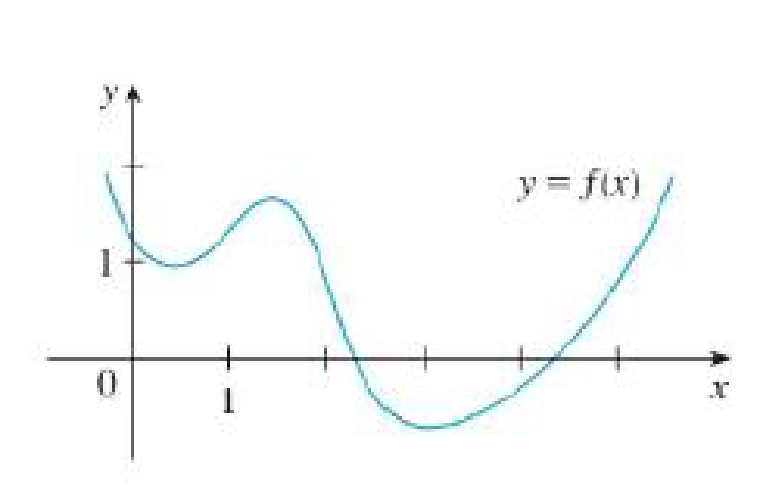
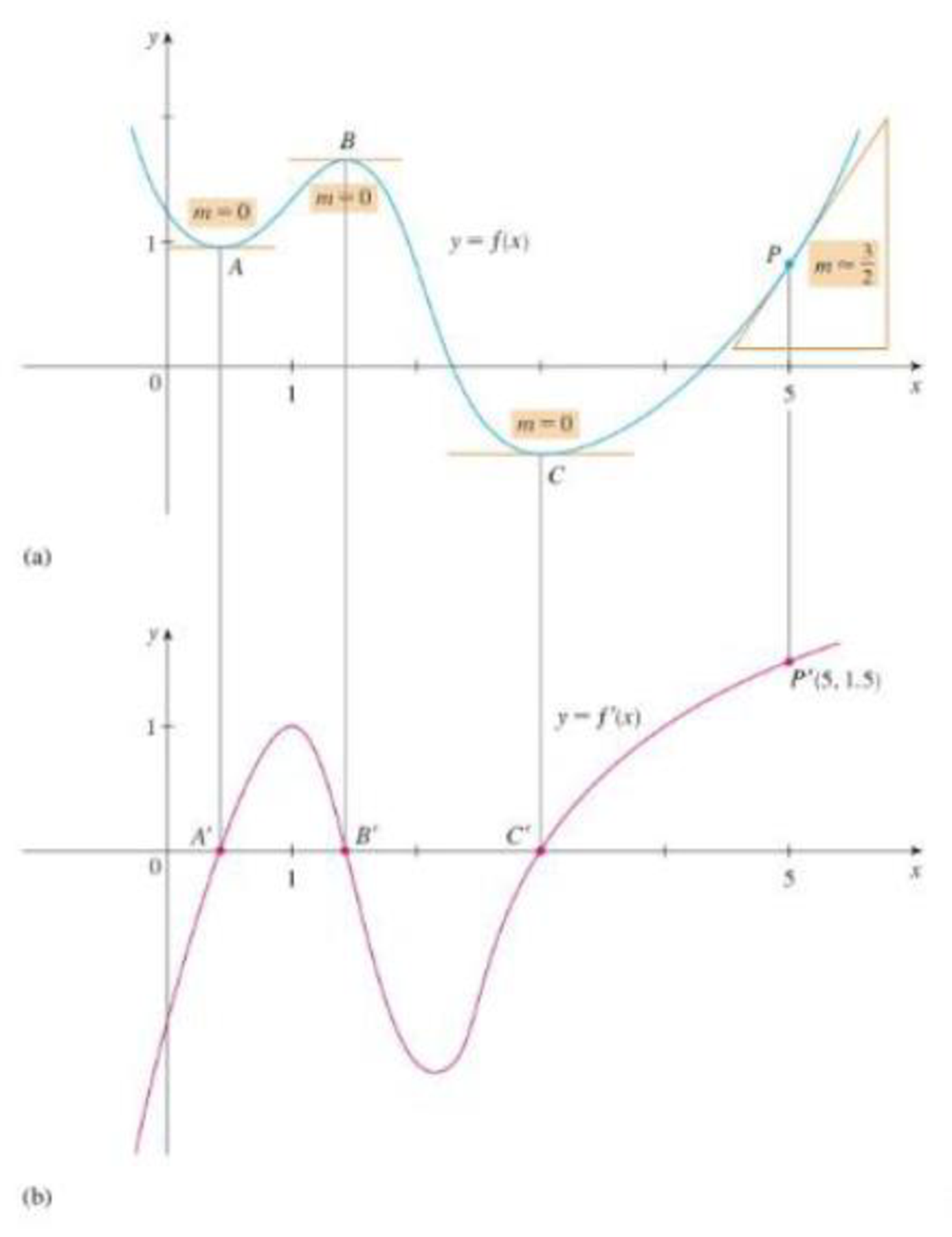
FIGURE 2
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Do the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.
纟
W₂
Find
S-FX SB.MX
4.
The revenue (in thousands of dollars) from producing x units of an item is R(x)=8x-0.015 x².
a) Find the average rate of change of revenue when the production is increased from 1000 to 1001 units.
Chapter 2 Solutions
Essential Calculus: Early Transcendentals; MAC 2311 Sequence| MAC 2281Sequence USF (Essential Calculus)
Ch. 2.1 - (a) Find the slope of the tangent line to the...Ch. 2.1 - (a) Find the slope of the tangent line to the...Ch. 2.1 - Find an equation of the tangent line to the curve...Ch. 2.1 - Find an equation of the tangent line to the curve...Ch. 2.1 - Find an equation of the tangent line to the curve...Ch. 2.1 - Find an equation of the tangent line to the curve...Ch. 2.1 - (a) Find the slope of the tangent to the curve y =...Ch. 2.1 - (a) Find the slope of the tangent to the curve...Ch. 2.1 - The graph shows the position function of a car....Ch. 2.1 - Shown are graphs of the position functions of two...
Ch. 2.1 - If a ball is thrown into the air with a velocity...Ch. 2.1 - If an arrow is shot upward on the moon with a...Ch. 2.1 - The displacement (in meters) of a particle moving...Ch. 2.1 - The displacement (in meters) of a particle moving...Ch. 2.1 - Prob. 15ECh. 2.1 - Find an equation of the tangent line to the graph...Ch. 2.1 - If an equation of the tangent tine to the curve y...Ch. 2.1 - If the tangent line to y= f(x) at (4, 3) passes...Ch. 2.1 - Sketch the graph of a function f for which f(0) =...Ch. 2.1 - Sketch the graph of a function g for which g(0) =...Ch. 2.1 - If f(x) = 3x2 x3 , find f'(l) and use it to find...Ch. 2.1 - Prob. 22ECh. 2.1 - (a) If F(x) = 5x/(l + x2), find F'(2) and use it...Ch. 2.1 - Prob. 24ECh. 2.1 - Find f'(a). f(x) = 3x2 4x + 1Ch. 2.1 - Find f'(a). f(t) = 2t3 + tCh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Each limit represents the derivative of some...Ch. 2.1 - Each limit represents the derivative of some...Ch. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - 3136 Each limit represents the derivative of some...Ch. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - The number N of US cellular phone subscribers (in...Ch. 2.1 - The number N of locations of a popular coffeehouse...Ch. 2.1 - Prob. 41ECh. 2.1 - If a cylindrical tank holds 100,000 gallons of...Ch. 2.1 - The cost of producing x ounces of gold from a new...Ch. 2.1 - The number of bacteria after r hours in a...Ch. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - The graph shows the influence of the temperature T...Ch. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.2 - Use the given graph to estimate the value of each...Ch. 2.2 - Use the given graph to estimate the value of each...Ch. 2.2 - Match the graph of each function in (a)(d) with...Ch. 2.2 - Trace or copy the graph of the given function .f....Ch. 2.2 - Trace or copy the graph of the given function .f....Ch. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Trace or copy the graph of the given function .f....Ch. 2.2 - Trace or copy the graph of the given function .f....Ch. 2.2 - Shown is the graph of the population function P(t)...Ch. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Find the derivative of the function using the...Ch. 2.2 - Find the derivative of the function using the...Ch. 2.2 - Find the derivative of the function using the...Ch. 2.2 - Find the derivative of the function using the...Ch. 2.2 - Find the derivative of the function using the...Ch. 2.2 - Find the derivative of the function using the...Ch. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - The unemployment rate U(t) varies with time. The...Ch. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - The graph of f is given. State, with reasons, the...Ch. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Use the definition of a derivative to find f'(x)...Ch. 2.2 - Prob. 42ECh. 2.2 - If f(x) = 2x2 x3, find f'(x), f"(x), f'"(x), and...Ch. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Where is the greatest integer function f(x) = [[ x...Ch. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.3 - Differentiate the function. f(x) = 240Ch. 2.3 - Differentiate the function. f(x)=2Ch. 2.3 - Differentiate the function. f(t)=223tCh. 2.3 - Differentiate the function. F(x)=34x8Ch. 2.3 - Prob. 5ECh. 2.3 - Differentiate the function. f(t) = 1.4t5 2.5t2+...Ch. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Differentiate the function. B(y) = cy6Ch. 2.3 - Differentiate the function. A(s)=12s5Ch. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Differentiate the function. y=x(x1)Ch. 2.3 - Prob. 17ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 18ECh. 2.3 - Differentiate the function. z=Ay10+BcosyCh. 2.3 - Prob. 22ECh. 2.3 - Differentiate the function. y=x2+4x+3xCh. 2.3 - Differentiate the function. y=sin2+cCh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 55ECh. 2.3 - Find the points on the curve y = 2x3 + 3x2 12x +...Ch. 2.3 - Prob. 37ECh. 2.3 - Show that the curve y = 6x3 + 5x 3 has no tangent...Ch. 2.3 - Find an equation of the tangent line to the curve...Ch. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 65ECh. 2.3 - Prob. 64ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 67ECh. 2.3 - Prob. 66ECh. 2.3 - For what values of a and b is the line 2x + y = b...Ch. 2.3 - Prob. 68ECh. 2.3 - Prob. 69ECh. 2.3 - Draw a diagram showing two perpendicular lines...Ch. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - If a ball is thrown vertically upward with a...Ch. 2.3 - If a rock is thrown vertically upward from the...Ch. 2.3 - The position function of a particle is given by s...Ch. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 51ECh. 2.3 - The cost function for production of a commodity is...Ch. 2.4 - Find the derivative of f(x) = (1 + 2x2)(x x2) in...Ch. 2.4 - Find the derivative o f the function...Ch. 2.4 - Differentiate. g(t)=t3costCh. 2.4 - Differentiate. f(x)=xsinxCh. 2.4 - Differentiate. g(x)=1+2x34xCh. 2.4 - Differentiate. G(x)=x222x+1Ch. 2.4 - Differentiate. h()=csccotCh. 2.4 - Differentiate. J(v) = (v3 2v)(v4 + v2)Ch. 2.4 - Prob. 5ECh. 2.4 - Differentiate. y=sincosCh. 2.4 - Differentiate. y=x31x2Ch. 2.4 - Differentiate. y=x+1x3+x2Ch. 2.4 - Differentiate. y=v32vvvCh. 2.4 - Differentiate. g(t)=ttt1/3Ch. 2.4 - Differentiate. f(t)=2t2+tCh. 2.4 - Differentiate. y=x1x+1Ch. 2.4 - Differentiate. f()=sec1+secCh. 2.4 - Differentiate. y=1secxtanxCh. 2.4 - Prob. 24ECh. 2.4 - Differentiate. f(x)=xx+cxCh. 2.4 - Find an equation of the tangent line to the given...Ch. 2.4 - Find an equation of the tangent line to the given...Ch. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - If f and g are the functions whose graphs are...Ch. 2.4 - Let P(x) = F(x)G(x) and Q(x) = F(x)/G(x), where F...Ch. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.4 - Prob. 53ECh. 2.4 - Prob. 54ECh. 2.4 - Prob. 55ECh. 2.4 - Prob. 56ECh. 2.4 - Prob. 57ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 7ECh. 2.4 - Differentiate. y = 2 sec x csc xCh. 2.4 - Prob. 19ECh. 2.4 - Differentiate. y=cosx1sinxCh. 2.4 - Prob. 23ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Find an equation of the tangent line to the curve...Ch. 2.4 - Prob. 30ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 40ECh. 2.4 - A mass on a spring vibrates horizontally on a...Ch. 2.4 - Prob. 52ECh. 2.4 - Prob. 36ECh. 2.5 - Write the composite function in the form f(g(x))....Ch. 2.5 - Write the composite function in the form f(g(x))....Ch. 2.5 - Write the composite function in the form f(g(x))....Ch. 2.5 - Write the composite function in the form f(g(x))....Ch. 2.5 - Write the composite function in the form f(g(x))....Ch. 2.5 - Write the composite function in the form f(g(x))....Ch. 2.5 - Find the derivative of the function. F(x) = (x4 +...Ch. 2.5 - Find the derivative of the function. F(x) = (4x ...Ch. 2.5 - Find the derivative of the function. F(x)=12xCh. 2.5 - Find the derivative of the function....Ch. 2.5 - Prob. 11ECh. 2.5 - Find the derivative of the function. f(t)=1+tant3Ch. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Find the derivative of the function. f(x) = (2x ...Ch. 2.5 - Find the derivative of the function. g(x) = (x2 +...Ch. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Find the derivative of the function. y=(x2+1x21)3Ch. 2.5 - Find the derivative of the function. f(s)=s2+1s2+4Ch. 2.5 - Find the derivative of the function. y=sin(xcosx)Ch. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Find the derivative of the function. y = cot2(sin...Ch. 2.5 - Prob. 36ECh. 2.5 - 742 Find the derivative of the function. 37....Ch. 2.5 - Find the derivative of the function. y=x+x+xCh. 2.5 - Prob. 39ECh. 2.5 - 742 Find the derivative of the function. 40....Ch. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - A table of values for f, g, f, and g is given. (a)...Ch. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Prob. 66ECh. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Air is being pumped into a spherical weather...Ch. 2.5 - Prob. 72ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 74ECh. 2.5 - Use the Chain Rule to show that if is measured in...Ch. 2.5 - Prob. 78ECh. 2.5 - Prob. 77ECh. 2.6 - (a) Find y by implicit differentiation. (b) Solve...Ch. 2.6 - (a) Find y by implicit differentiation. (b) Solve...Ch. 2.6 - Find dy/dx by implicit differentiation. x3 + y3 =...Ch. 2.6 - Find dy/dx by implicit differentiation. 2x3 + x2y ...Ch. 2.6 - Prob. 5ECh. 2.6 - Find dy/dx by implicit differentiation. y5 + x2y3...Ch. 2.6 - Find dy/dx by implicit differentiation. 11. y cos...Ch. 2.6 - Find dy/dx by implicit differentiation. 12....Ch. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Find dy/dx by implicit differentiation. x+y=1+x2y2Ch. 2.6 - 3-16 Find dy/dx by implicit differentiation. 13....Ch. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Find dy/dx by implicit differentiation. 20....Ch. 2.6 - Prob. 17ECh. 2.6 - If g(x) + x sin g(x) = x2, find g(0).Ch. 2.6 - Use implicit differentiation to find an equation...Ch. 2.6 - Prob. 19ECh. 2.6 - Use implicit differentiation to find an equation...Ch. 2.6 - Prob. 22ECh. 2.6 - Use implicit differentiation to find an equation...Ch. 2.6 - Prob. 24ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Find the points on the lemniscate in Exercise 23...Ch. 2.6 - Show by implicit differentiation that the tangent...Ch. 2.6 - Show that the sum of the x-and y-intercepts of any...Ch. 2.6 - Prob. 41ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.7 - Prob. 1ECh. 2.7 - (a) If A is the area of a circle with radius r and...Ch. 2.7 - Prob. 3ECh. 2.7 - The length of a rectangle is increasing at a rate...Ch. 2.7 - A cylindrical tank with radius 5 m is being filled...Ch. 2.7 - The radius of a sphere is increasing at a rate of...Ch. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - A particle is moving along a hyperbola xy = 8. As...Ch. 2.7 - Prob. 13ECh. 2.7 - (a) What quantities are given in the problem? (b)...Ch. 2.7 - (a) What quantities are given in the problem? (b)...Ch. 2.7 - (a) What quantities are given in the problem? (b)...Ch. 2.7 - Two cars start moving from the same point. One...Ch. 2.7 - A spotlight on the ground shines on a wall 12m...Ch. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 24ECh. 2.7 - A trough is 10 ft long and its ends have the shape...Ch. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 37ECh. 2.7 - A lighthouse is located on a small island 3 km...Ch. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.8 - Find the linearization L(x) of the function at a....Ch. 2.8 - Prob. 2ECh. 2.8 - Prob. 3ECh. 2.8 - Prob. 4ECh. 2.8 - Prob. 5ECh. 2.8 - Prob. 6ECh. 2.8 - Prob. 7ECh. 2.8 - Prob. 10ECh. 2.8 - 7-10 Verify the given linear approximation at a =...Ch. 2.8 - Prob. 8ECh. 2.8 - Prob. 18ECh. 2.8 - Prob. 17ECh. 2.8 - Let y = tan x. (a) Find the differential dy. (b)...Ch. 2.8 - Let y = tan x. (a) Find the differential dy. (b)...Ch. 2.8 - Prob. 11ECh. 2.8 - Prob. 14ECh. 2.8 - Use a linear approximation (or differentials) to...Ch. 2.8 - Prob. 13ECh. 2.8 - Prob. 15ECh. 2.8 - Prob. 16ECh. 2.8 - Prob. 21ECh. 2.8 - Prob. 22ECh. 2.8 - The circumference of a sphere was measured to be...Ch. 2.8 - Prob. 24ECh. 2.8 - One side of a right triangle is known to be 20 cm...Ch. 2.8 - Prob. 25ECh. 2.8 - When blood flows along a blood vessel, the flux F...Ch. 2.8 - Prob. 28ECh. 2.8 - Prob. 29ECh. 2.8 - Suppose that we dont have a formula for g(x) but...Ch. 2 - Prob. 1RCCCh. 2 - Prob. 2RCCCh. 2 - Prob. 4RCCCh. 2 - Prob. 3RCCCh. 2 - Prob. 5RCCCh. 2 - Prob. 6RCCCh. 2 - Prob. 7RCCCh. 2 - Prob. 1RQCh. 2 - Prob. 8RQCh. 2 - Determine whether the statement is true or false....Ch. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 63RECh. 2 - Prob. 7RECh. 2 - Prob. 9RECh. 2 - Prob. 8RECh. 2 - Prob. 8RCCCh. 2 - Prob. 9RCCCh. 2 - Prob. 10RCCCh. 2 - Prob. 11RCCCh. 2 - Prob. 2RQCh. 2 - Prob. 3RQCh. 2 - Prob. 4RQCh. 2 - Prob. 5RQCh. 2 - Prob. 6RQCh. 2 - Prob. 12RQCh. 2 - Prob. 7RQCh. 2 - Prob. 11RQCh. 2 - Prob. 9RQCh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 19RECh. 2 - Prob. 33RECh. 2 - Prob. 1RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 18RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 24RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 39RECh. 2 - Prob. 35RECh. 2 - Prob. 32RECh. 2 - Prob. 34RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - 70. If f and g are the functions whose graphs are...Ch. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 57RECh. 2 - Prob. 56RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 65RECh. 2 - Prob. 64RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Evaluate limx01+tanx1+sinxx3.Ch. 2 - Prob. 80RECh. 2 - Prob. 81RECh. 2 - Prob. 82RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- MATH 122 WORKSHEET 3 February 5, 2025 . Solve the following problems on a separate sheet. Justify your answers to earn full credit. 1. Let f(x) = x² - 2x + 1. (a) Find the slope of the graph of y = f (x) at the point P = (0,1) by directly evaluating the limit: f'(0) = lim ( f(Ax) - f(0) Ax Ax→0 (b) Find the equation of the tangent line 1 to the graph of ƒ at P. What are the x and y intercepts of 1 ? (c) Find the equation of the line, n, through P that is perpendicular to the tangent line l. (Line n is called the normal line to the graph of f at P.) (d) Sketch a careful graph that displays: the graph of y = f (x), its vertex point, its tangent and normal lines at point P, and the x and y intercepts of these lines. Bonus: Find the coordinates of the second point, Q, (QP), at which the normal line n intersects the graph of f. 2. A rock is thrown vertically upward with an initial velocity of 20 m/s from the edge of a bridge that is 25 meters above a river bed. Based on Newton's Laws of…arrow_forward3. Use the graph for problem #35, p175 to answer the questions. The average price (in cents) per gallon of unleaded gasoline in the United States for the years 2010 to 2019 is shown in this chart. Find the average rate of change per year in the average price per gallon for each time period. Source: U.S. Energy Information Administration. a) 2010 to 2013 b) 2012 to 2018 c) 2014 to 2019arrow_forward4. Researchers at Iowa State University and the University of Arkansas have developed a piecewise function that can be used to estimate the body weight (in grams) of a male broiler during the first 56 days of life according to W(t)=48+3.64t+0.6363²+0.00963 t³ if 1St≤28, -1004+65.8t if 28arrow_forward3. Given the function h(x)=(x²+x-12 if x≤1 3-x if x>1' a) Graph the function h(x). Make the graph big enough to be easily read using the space below. Be sure to label all important aspects of the graph. b) Find all values of x where the function is discontinuous. c) Find the limit from the left and from the right at any values of x found in part b.arrow_forward2. Find the instantaneous rate of change for each function f(x)=2x²-x+3 at x=0..arrow_forward4x-3 2. Determine the interval over which the function is continuous. x+4arrow_forward1. Find the average rate of change for the following functions over the given intervals. a) f(x)=4x-2x²+3x between x=-1 and x=4 b) y lnx between x=1 and x=4arrow_forward1. Find all values x=a where the function is discontinuous, determine if the discontinuity is removable or non- removable. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist and explain how you know. a) f(x)= 2-x x²(x+5) b) f(x)= x²-9x x²+3x c) p(x)=-3x²+2x²+5x-8arrow_forwardDo the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.arrow_forward12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.508.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x + 16 dx X Need Help? Read It SUBMIT ANSWER 13. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.512.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx 8)(2x + 1) Need Help? Read It SUBMIT ANSWER 14. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.518.XP. Find the area of the region under the given curve from 1 to 5. y = x² +7 6x - x² Need Help? Read It ASK YOUR TEAarrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.012. 6. [-/1 Points] Evaluate the integral. x-4 dx x² - 5x + 6 Need Help? Read It SUBMIT ANSWER 7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.019. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x²+1 (x-6)(x-5)² dx Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.021. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ✓ x² 4 +4 dxarrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.017. 1. [-/1 Points] Evaluate the integral. - - dy y(y + 2)(y-3) Need Help? Read It Watch It SUBMIT ANSWER 2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.027. Evaluate the integral. (Use C for the constant of integration.) X + 16 x²+10x29 dx Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY