Chapter 2.1, Problem 79E

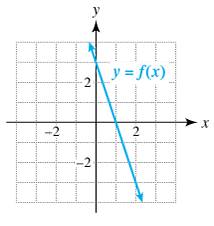
Exercises 77−82: Use the graph of $y=f\left(x\right)$ to complete the following.

a. Identity the x- and y-intercepts.

b. Find the slop of the graph.

c. Give any zeros of $f$ .

d. Identity the interval(s) where $f$ is positive or negative.

e. Identity the interval(s) where $f$ is increasing or decreasing. Is $f$ ever increasing and negative on the same interval? Is $f$ ever decreasing and positive on the same Interval?

f. Find the slope-intercept form for $y=f\left(x\right)$ . Can tell from the slope-intercept form if $f$ is increasing or decreasing? Explain

79.