Chapter 21, Problem 107GQ

A Boron and hydrogen form an extensive family of compounds, and the diagram below shows how they are related by reaction.

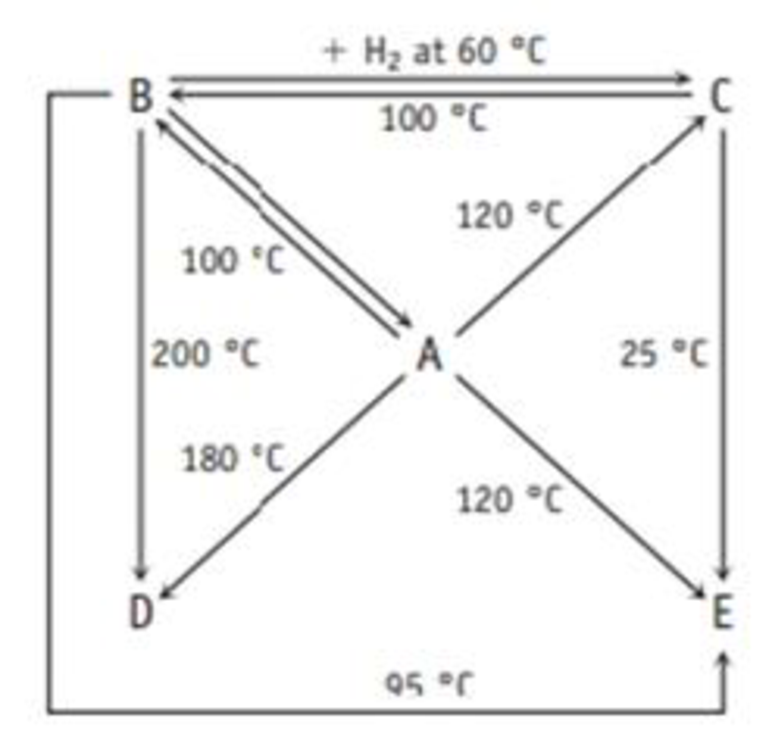
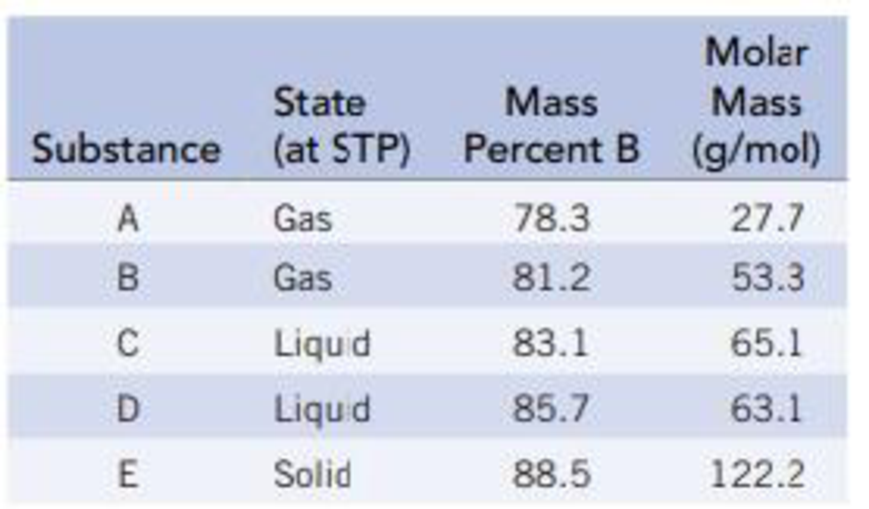
The following table gives the weight percent of boron in each of the compounds. Derive the empirical and molecular formulas of compounds A-E.

Interpretation Introduction

Interpretation: To determine the empirical and molecular formula of given compounds A-E.

Concept introduction:

The empirical formula of a chemical compound is the simplest positive integer ratio of atoms present in a compound.

A molecular formula shows the total number of atoms in a molecule but not their structural arrangement.

Answer to Problem 107GQ

The empirical formula of compound A is ${\text{BH}}_{\text{3}}$ and the molecular formula of compound A is ${\text{B}}_{\text{2}}{\text{H}}_{\text{6}}$.

The empirical formula of compound B is ${\text{BH}}_{2.5}$ and the molecular formula of compound B is ${\text{B}}_4{\text{H}}_{10}$.

The empirical formula of compound C is ${\text{BH}}_{2.2}$ and the molecular formula of compound C is ${\text{B}}_5{\text{H}}_{11}$.

The empirical formula of compound D is ${\text{BH}}_{1.78}$ and the molecular formula of compound D is ${\text{B}}_5{\text{H}}_9$.

The empirical formula of compound E is ${\text{BH}}_{1.4}$ and the molecular formula of compound E is ${\text{B}}_{10}{\text{H}}_{14}$.

Explanation of Solution

Boron and hydrogen form an extensive family of compounds. Substance A-E contains boron and hydrogen atoms.

The empirical and molecular formula of given compounds A-E is calculated below.

Given:

Substance A is a gaseous compound contains $78.3\%$ by mass of boron and $21.7\%$ by mass of hydrogen. The molecular weight of boron is $10.8\text{g}\cdot {\text{mol}}^{-1}$ and the molecular weight of hydrogen atom is $1.008\text{g}\cdot {\text{mol}}^{-1}$.

The empirical formula of substance A is calculated as,

Convert the mass of boron and hydrogen into moles using molar mass of boron and hydrogen respectively.

$\begin{array}{l}\frac{78.3\text{g}}{10.8\text{g}\cdot {\text{mol}}^{-1}}=7.25\text{mol}\text{boron}\\ \frac{21.7\text{g}}{1.008\text{g}\cdot {\text{mol}}^{-1}}=21.5\text{mol}\text{hydrogen}\end{array}$

Divide each mole value by the smallest number of moles calculated. Round off to the nearest whole number.

$\begin{array}{l}\frac{7.25\text{mol}\text{boron}}{7.25\text{mol}}=1.00\\ \frac{21.5\text{mol}\text{hydrogen}}{7.25\text{mol}}\approx 3.00\end{array}$

Thus, the empirical formula of compound A is ${\text{BH}}_{\text{3}}$.

The empirical formula molar mass of compound A is $13.82\text{g}\cdot {\text{mol}}^{-1}$ and the molecular formula molar mass of compound A is $27.7\text{g}\cdot {\text{mol}}^{-1}$.

Divide the molecular formula mass by the empirical formula mass,

$\frac{27.7\text{g}\cdot {\text{mol}}^{-1}}{13.8\text{g}\cdot {\text{mol}}^{-1}}=2.00$

Multiply each of the subscripts within the empirical formula of substance A by the number calculated above.

Thus, the molecular formula of substance A is $2\left({\text{BH}}_{\text{3}}\right)$ that is ${\text{B}}_{\text{2}}{\text{H}}_{\text{6}}$.

Substance B is a gaseous compound contains $81.2\%$ by mass of boron and $18.8\%$ by mass of hydrogen. The molecular weight of boron is $10.8\text{g}\cdot {\text{mol}}^{-1}$ and the molecular weight of hydrogen atom is $1.008\text{g}\cdot {\text{mol}}^{-1}$.

The empirical formula of substance B is calculated as,

Convert the mass of boron and hydrogen into moles using molar mass of boron and hydrogen respectively.

$\begin{array}{l}\frac{81.2\text{g}}{10.8\text{g}\cdot {\text{mol}}^{-1}}=7.52\text{mol}\text{boron}\\ \frac{18.8\text{g}}{1.008\text{g}\cdot {\text{mol}}^{-1}}=18.65\text{mol}\text{hydrogen}\end{array}$

Divide each mole value by the smallest number of moles calculated. Round off to the nearest whole number.

$\begin{array}{l}\frac{7.52\text{mol}\text{boron}}{7.52\text{mol}}=1.00\\ \frac{18.65\text{mol}\text{hydrogen}}{7.52\text{mol}}=2.5\end{array}$

Thus, the empirical formula of compound B is ${\text{BH}}_{2.5}$.

The empirical formula molar mass of compound B is $12.82\text{g}\cdot {\text{mol}}^{-1}$ and the molecular formula molar mass of compound B is $53.3\text{g}\cdot {\text{mol}}^{-1}$.

Divide the molecular formula mass by the empirical formula mass,

$\frac{53.3\text{g}\cdot {\text{mol}}^{-1}}{12.8\text{g}\cdot {\text{mol}}^{-1}}\approx 4.00$

Multiply each of the subscripts within the empirical formula of substance B by the number calculated above.

Thus, the molecular formula of substance B is $4\left({\text{BH}}_{2.5}\right)$ that is ${\text{B}}_4{\text{H}}_{10}$.

Substance C is a liquid compound contains $83.1\%$ by mass of boron and $16.9\%$ by mass of hydrogen. The molecular weight of boron is $10.8\text{g}\cdot {\text{mol}}^{-1}$ and the molecular weight of hydrogen atom is $1.008\text{g}\cdot {\text{mol}}^{-1}$.

The empirical formula of substance C is calculated as,

Convert the mass of boron and hydrogen into moles using molar mass of boron and hydrogen respectively.

$\begin{array}{l}\frac{83.1\text{g}}{10.8\text{g}\cdot {\text{mol}}^{-1}}=7.69\text{mol}\text{boron}\\ \frac{16.9\text{g}}{1.008\text{g}\cdot {\text{mol}}^{-1}}=16.76\text{mol}\text{hydrogen}\end{array}$

Divide each mole value by the smallest number of moles calculated. Round off to the nearest whole number.

$\begin{array}{l}\frac{7.69\text{mol}\text{boron}}{7.69\text{mol}}=1.00\\ \frac{16.76\text{mol}\text{hydrogen}}{7.69\text{mol}}\approx 2.2\end{array}$

Thus, the empirical formula of compound C is ${\text{BH}}_{2.2}$.

The empirical formula molar mass of compound A is $13.02\text{g}\cdot {\text{mol}}^{-1}$ and the molecular formula molar mass of compound C is $65.1\text{g}\cdot {\text{mol}}^{-1}$.

Divide the molecular formula mass by the empirical formula mass,

$\frac{65.1\text{g}\cdot {\text{mol}}^{-1}}{13.02\text{g}\cdot {\text{mol}}^{-1}}=5.00$

Multiply each of the subscripts within the empirical formula of substance C by the number calculated above.

Thus, the molecular formula of substance C is $5\left({\text{BH}}_{2.2}\right)$ that is ${\text{B}}_5{\text{H}}_{11}$.

Substance D is a liquid compound contains $85.7\%$ by mass of boron and $14.3\%$ by mass of hydrogen. The molecular weight of boron is $10.8\text{g}\cdot {\text{mol}}^{-1}$ and the molecular weight of hydrogen atom is $1.008\text{g}\cdot {\text{mol}}^{-1}$.

The empirical formula of substance D is calculated as,

Convert the mass of boron and hydrogen into moles using molar mass of boron and hydrogen respectively.

$\begin{array}{l}\frac{85.7\text{g}}{10.8\text{g}\cdot {\text{mol}}^{-1}}=7.93\text{mol}\text{boron}\\ \frac{14.3\text{g}}{1.008\text{g}\cdot {\text{mol}}^{-1}}=14.18\text{mol}\text{hydrogen}\end{array}$

Divide each mole value by the smallest number of moles calculated. Round off to the nearest whole number.

$\begin{array}{l}\frac{7.93\text{mol}\text{boron}}{7.93\text{mol}}=1.00\\ \frac{14.18\text{mol}\text{hydrogen}}{7.93\text{mol}}=1.78\end{array}$

Thus, the empirical formula of compound D is ${\text{BH}}_{1.78}$.

The empirical formula molar mass of compound A is $12.59\text{g}\cdot {\text{mol}}^{-1}$ and the molecular formula molar mass of compound D is $63.1\text{g}\cdot {\text{mol}}^{-1}$.

Divide the molecular formula mass by the empirical formula mass,

$\frac{63.1\text{g}\cdot {\text{mol}}^{-1}}{12.59\text{g}\cdot {\text{mol}}^{-1}}=5.00$

Multiply each of the subscripts within the empirical formula of substance D by the number calculated above.

Thus, the molecular formula of substance D is $5\left({\text{BH}}_{1.78}\right)$ that is ${\text{B}}_5{\text{H}}_9$.

Substance E is a solid compound contains $88.5\%$ by mass of boron and $11.5\%$ by mass of hydrogen. The molecular weight of boron is $10.8\text{g}\cdot {\text{mol}}^{-1}$ and the molecular weight of hydrogen atom is $1.008\text{g}\cdot {\text{mol}}^{-1}$.

The empirical formula of substance E is calculated as,

Convert the mass of boron and hydrogen into moles using molar mass of boron and hydrogen respectively.

$\begin{array}{l}\frac{88.5\text{g}}{10.8\text{g}\cdot {\text{mol}}^{-1}}=8.19\text{mol}\text{boron}\\ \frac{11.5\text{g}}{1.008\text{g}\cdot {\text{mol}}^{-1}}=11.41\text{mol}\text{hydrogen}\end{array}$

Divide each mole value by the smallest number of moles calculated. Round off to the nearest whole number.

$\begin{array}{l}\frac{8.19\text{mol}\text{boron}}{8.19\text{mol}}=1.00\\ \frac{11.41\text{mol}\text{hydrogen}}{8.19\text{mol}}=1.4\end{array}$

Thus, the empirical formula of compound E is ${\text{BH}}_{1.4}$.

The empirical formula molar mass of compound E is $12.11\text{g}\cdot {\text{mol}}^{-1}$ and the molecular formula molar mass of compound E is $122.2\text{g}\cdot {\text{mol}}^{-1}$.

Divide the molecular formula mass by the empirical formula mass,

$\frac{122.2\text{g}\cdot {\text{mol}}^{-1}}{12.11\text{g}\cdot {\text{mol}}^{-1}}=10$

Multiply each of the subscripts within the empirical formula of substance E by the number calculated above.

Thus, the molecular formula of substance E is $10\left({\text{BH}}_{1.4}\right)$ that is ${\text{B}}_{10}{\text{H}}_{14}$.

Conclusion

The empirical formula of compound A is ${\text{BH}}_{\text{3}}$ and the molecular formula of compound A is ${\text{B}}_{\text{2}}{\text{H}}_{\text{6}}$.

The empirical formula of compound B is ${\text{BH}}_{2.5}$ and the molecular formula of compound B is ${\text{B}}_4{\text{H}}_{10}$.

The empirical formula of compound C is ${\text{BH}}_{2.2}$ and the molecular formula of compound C is ${\text{B}}_5{\text{H}}_{11}$.

The empirical formula of compound D is ${\text{BH}}_{1.78}$ and the molecular formula of compound D is ${\text{B}}_5{\text{H}}_9$.

The empirical formula of compound E is ${\text{BH}}_{1.4}$ and the molecular formula of compound E is ${\text{B}}_{10}{\text{H}}_{14}$.