
a
To compute:The Value of a stock-plus-put position as on the ending date of the option.
Introduction:
Put-Call parity relationship: It is a relationship defined among the amounts of European put options and European call options of the given same class. The condition implied here is that the underlying asset, strike price, and expiration dates are the same in both the options. The Put-Call
Parity equation is as follows: 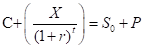
Where C= Call premium
P=Put premium
X=Strike Price of Call and Put
r=Annual interest rate
t= Time in years
S0= Initial price of underlying
b
To compute: The value of the portfolio as on the ending date of the option when portfolio includes a call option and zero-coupon bond with face value (X+D) and make sure its value equals the stock plus-put portfolio.
Introduction:
Value of the portfolio:It is also called as the portfolio value. The
c.
To compute: The cost of establishing above said portfolios and derives the put-call parity relationship.
Introduction:
Put-Call parity relationship: It is a relationship defined among the amounts of European put options and European call options of the given same class. The condition implied here is that the underlying asset, strike price, and expiration dates are the same in both the options. The Put-Call Parity equation is as follows: 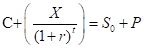
Want to see the full answer?
Check out a sample textbook solution
Chapter 20 Solutions
Investments
- critically discuss the hockey stick model of a start-up financing. In your response, explain the model and discibe its three main stages, highlighting the key characteristics of each stage in terms of growth, risk, and funding expectations.arrow_forwardSolve this problem please .arrow_forwardSolve this finance question.arrow_forward
- solve this question.Pat and Chris have identical interest-bearing bank accounts that pay them $15 interest per year. Pat leaves the $15 in the account each year, while Chris takes the $15 home to a jar and never spends any of it. After five years, who has more money?arrow_forwardWhat is corporate finance? explain all thingsarrow_forwardSolve this finance problem.arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





