Problem 1RQ: Review Question 2.1 What does the statement “Motion is relative” mean?
Problem 2RQ: Review Question 2.2 Is the following statement true? If an objects velocity change arrows point to... Problem 3RQ: Review Question 2.3 Eugenia says that to find the v arrow on a motion diagram you need to subtract... Problem 4RQ: Review Question 2.4 Jade went hiking between two camps that were separated by about 10 km. She hiked... Problem 5RQ: Review Question 2.5 A position- versus-time graph representing a moving object is shown in Figure... Problem 6RQ: Review Question 2.6 Why is the following statement true? Displacement is equal to the area between a... Problem 7RQ: Review Question 2.7 (a) Give an example in which an object with negative acceleration is speeding... Problem 8RQ: Review Question 2.8 Explain qualitatively, without algebra, why the displacement of an object moving... Problem 9RQ: Review Question 2.9 A cars motion with respect to the ground is described by the following function:... Problem 1MCQ: Match the general elements or physics knowledge (left) with the appropriate examples (right). Model... Problem 2MCQ: Which group of quantities below consists only of scalar quantities? a. Average speed, displacement,... Problem 3MCQ: Which of the following are examples of time interval? (1) I woke up at 7 a.m. (2) The lesson lasted... Problem 4MCQ: A student said. The displacement between my dorm and the lecture hall is 1 kilometer. Is he using... Problem 5MCQ: An object moves so that its position depends on time as x=+12m(4m/s)t+(1m/s2)t2. Which statement... Problem 6MCQ: 6. Choose the correct approximate velocity-versus-time graph for the following hypothetical motion:... Problem 7MCQ: Figure Q2.7b shows the position-versus-time graph for a small red dot that was moving along the... Problem 8MCQ: Oilver takes two identical marbles and drops the first one from a certain height. A short time... Problem 9MCQ: 9. Your car is traveling west at 12 m/s. A stoplight (the origin of the coordinate axis) to the west... Problem 10MCQ: Which velocity-versus-time graph in Figure Q2.10 best describes the motion of the car in the... Problem 11MCQ: 11. Azra wants to determine the average speed of the high-speed train that operates between Paris... Problem 12MCQ: A sandbag hangs from a rope attached to a rising hot air balloon. The rope connecting the bag to the... Problem 13MCQ: An apple falls from a tree. It hits the ground at a speed of about 5.0 m/s. What is the approximate... Problem 14MCQ: 14. You have two small metal balls. You drop the first ball and throw the other one in the downward... Problem 15MCQ: Which of the graphs in Figure Q2.15 represent the motion of an object that starts from rest and... Problem 16MCQ:
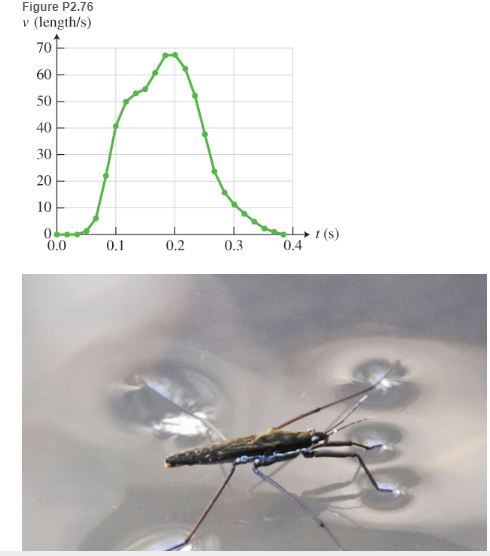
16. You throw a small ball upward and notice the time it takes to come back. If you then throw the... Problem 17CQ: Figure Q2.17 shows vectors E,F, and G. Draw the following vectors using rules for graphical addition... Problem 18CQ: Peter is cycling along an 800-m straight stretch of a track. His speed is 13 m/s. Choose all of the... Problem 19CQ: In what reasonable ways can you represent or describe the motion of a car traveling from one... Problem 20CQ: What is the difference between speed and velocity? Between path length and distance? Between... Problem 21CQ: 21. What physical quantities do we use to describe motion? What does each quantity characterize?... Problem 22CQ: 22. Devise stories describing each of the motions shown in each of the graphs in Figure Q2.22.... Problem 23CQ: 23. For each of the position-versus-time graphs in Figure Q2.23, draw velocity-versus-time graphs... Problem 24CQ: Figure Q2.24 shows velocity-versus-time graphs for two objects. A and B. Draw motion diagrams that... Problem 25CQ: Can an object have a nonzero velocity and zero acceleration? If so, give an example. Problem 26CQ: 26. Can an object at one instant of time have zero velocity and nonzero acceleration? If so, give an... Problem 27CQ: 27. Your little sister has a battery-powered toy truck. When the truck is moving, how can you... Problem 28CQ: You throw a ball upward. Your friend says that at the top of its flight the ball has zero velocity... Problem 1P: A car starts at rest from a stoplight and speeds up. It then moves at constant speed for a while.... Problem 2P: * You are an observer on the ground. (a) Draw two motion diagrams representing the motions of two... Problem 3P: 3. * A car is moving at constant speed on a highway. A second car catches up and passes the first... Problem 4P: 4. * A hat falls off a man’s head and lands in the snow. Draw a motion diagram representing the... Problem 5P: 5 Figure P2.5 shows several displacement vectors that are all in the (x, y) plane. (a) List all... Problem 6P: 6. Figure P.26 shows an incomplete motion diagram for an object (a) For each pair of adjacent... Problem 7P: 7. * You drive 100 Km east do some sightseeing and then turn around and drive 50 Km west where you... Problem 8P: * Choose an object or reference and a set of coordinate axes associated with it. Show how two people... Problem 9P: The scalar x-component of a displacement vector for a trip is -70 km. Represent the trip using a... Problem 10P: 10. * You recorded your position with respect to the front door of your house as you walked to the... Problem 11P: * You need to determine the time interval (in seconds) needed for light to pass an atomic nucleus.... Problem 12P: A speedometer reads 65 ml/h. (a) Use as many different units as possible to represent the speed of... Problem 13P: 13. Convert the following record speeds so that they are in ml/h, km/h. and m/s. (a) Australian... Problem 15P: 15. * BIO A kidnapped banker looking through a slit in a van window counts her heartbeats and... Problem 16P: 16 * Some computer scanners scan documents by moving the scanner head with a constant speed across... Problem 18P: 18. * Your friend’s pedometer shows that he took 17,000 steps in 2.50 h during a hike. Determine... Problem 19P: During a hike, two friends were caught in a thunderstorm. Four seconds after seeing lightning from a... Problem 20P: 20. Light travels at a speed of m/s in a vacuum. The approximate distance between Earth and the Sun... Problem 21P: 21. Proxima Centauri is light-years from Earth. Determine the length of 1 light-year and convert the... Problem 22P: * Spaceships traveling to other planets in the solar system move at an average speed of 1.1104 m/s.... Problem 23P: 23. ** Figure P2.23 shows a velocity-versus-time graph for the bicycle trips of two friends with... Problem 24P: 24. * Table 2.9 shows position and time data for your walk along a straight path. (a) Tell... Problem 25P: 25. * Table 2.10 shows position and time data for your friend’s bicycle ride along a straight bike... Problem 26P: 26 * You are walking to your physics class at speed 1.0 m/s with respect to the ground. Your friend... Problem 27P: * Gabriele enters an east-west straight bike path at the 3.0-km mark and rides west at a constant... Problem 28P: * Jim is driving his car at 32 m/s (72 mi/h) along a highway where the speed limit is 25 m/s (55... Problem 29P: 29. * You hike two-thirds of the way to the top or a hill at a speed or 3.0 ml/h and run the final... Problem 30P: 30. * Olympic champion swimmer Michael Phelps swam at an average speed of 2.01 m/s during the first... Problem 31P: 31. * A car makes a 100-Km trip. it travels the first 50 Km at an average speed of 50 km/h. how fast... Problem 32P: * Jane and Bob see each other when 100m apart. They are moving forward each other, Jane at constant... Problem 34P: 34. A car starts from rest and reaches the speed of 10 m/s in 30 s. What can you determine about the... Problem 35P: A truck is traveling east at +16 m/s (a) The driver sees that the road is empty and accelerates at... Problem 36P: 36. Bumper car collision on a bumper car ride, friends smash their cars into each other (head-on),... Problem 37P: A bus leaves an intersection accelerating at +2.0 m/s2. Where is the bus after 5.0 s? What... Problem 38P: A jogger is running at +4.0 m/s when a bus passes her. The bus is accelerating from +16.0 m/s to +... Problem 39P: 39. * The motion of a person as seen by another person is described by the equation (a) Represent... Problem 40P: While cycling at a speed of 10 m/s, a cyclist starts going downhill with an acceleration of... Problem 41P: * EST To his surprise, Daniel found that an egg did not break when he accidentally dropped it from a... Problem 42P: 42. BIO Squid propulsion Lolliguncula brevis squid use a form of jet propulsion to swim-they eject... Problem 43P: Dragster record on the desert In 1977, Kitty ONell drove a hydrogen peroxide-powered rocket dragster... Problem 44P: * Imagine that a sprinter accelerates from rest to a maximum speed of 10.8 m/s in 1.8 s. In what... Problem 45P: 45. ** Two runners are running next to each other when one decides to speed up at constant... Problem 46P: 46. * Meteorite hits car in 1992, a 14-kg meteorite struck a car in Peekskill, NY, leaving a... Problem 47P: 47. BIO Froghopper jump A spittlebug called the froghopper (Philaenus spumarius) is believed to be... Problem 48P: 48. Tennis serve The fastest server in women’s tennis is Sabine Lisicki, who recorded a serve of 131... Problem 49P: 49. * Shot from a cannon in 1998, David “Cannonball” Smith set the distance record for being shot... Problem 50P: Col. John Stapps final sied run Col. John Stapp led the U.S. Air Force Acro Medical Laboratorys... Problem 51P: 51. * Sprinter Usain Bolt reached a maximum speed of 11.2 m/s in 2.0 s while running the 100-m dash.... Problem 52P: ** Imagine that Usain Bolt can reach his maximum speed in 1.7s. What should be his maximum speed in... Problem 53P: * A bus is moving at a speed of 36 km/h. How far from a bus stop should the bus start to slow down... Problem 54P: * EST You want to estimate how fast your car accelerates. What information can you collect to answer... Problem 55P: * In your car, you covered 2.0 m during the first 1.0 s, 4.0 m during the second 1.0 s, 6.0 m during... Problem 56P: 56. (a) Determine the acceleration of a car in which the velocity changes from -10m/s to -20m/s in... Problem 57P: You accidentally drop an eraser out the window of an apartment 15 m above the ground. (a) How long... Problem 58P: 58. * What is the average speed of the eraser in the previous problem from the instant it is... Problem 59P: 59. You throw a tennis ball straight upward. The initial speed is about 12m/s. Say everything you... Problem 60P: 60. While skydiving, your parachute opens and you slow from 50.0 m/s to 8.0 m/s in 0.80s. Determine... Problem 61P: * After landing from your skydiving experience, you are so excited that you throw your helmet... Problem 62P: * You are standing on the rim of a canyon. You drop a rock and in 7.0 s hear the sound of it hitting... Problem 63P: 63. * You are doing an experiment to determine your reaction time. Your friend holds a ruler. You... Problem 64P: EST Cliff divers Divers in Acapulco fall 36m from a cliff into the water. Estimate their speed when... Problem 65P: 65. * Galileo dropped a light rock and a heavy rock from the Learning Tower of Pisa, which is about... Problem 66P: * A person holding a lunch bag is moving upward in a hot air balloon at a constant speed of 7.0 m/s.... Problem 67P: * A parachutist falling vertically at a constant speed of 10m/s drops a penknife when 20 m above the... Problem 68P: A diagram representing the motion of two cars is shown in Figure P2.68. The number near each dot... Problem 69P: Use the velocity-versus-time graph lines in Figure P2.69 to determine the change in the position of... Problem 71P: * While babysitting their younger brother, Chrisso and Devin are playing with toys. They notice that... Problem 72P: 72. ** An object moves so that its position changes in the following way: . (a) What kind of motion... Problem 73P: * The positions of objects A and B with respect to Earth depend on time as follows:... Problem 74P: * Two cars on a straight road at time zero are beside each other. The first car, traveling at speed... Problem 75P: 75. * Oliver drops a tennis ball from a certain height above a concrete floor. Figure P2.75 shows... Problem 76P: 76. * BIO EST Water striders Water striders are insects that propel themselves on the surface of... Problem 77P: 77. You are traveling in your car at 20 m/s a distance of 20 m behind a car traveling at the same... Problem 78P: * You are driving a car behind another car. Both cars are moving at speed 80 km/h. What minimum... Problem 79P: 79. * A driver with a 0.80-s reaction time applies the brakes, causing the car to have 7.0-m/s2... Problem 80P: 80. ** Some people in a hotel are dropping water balloons from their open window onto the ground... Problem 81P: s acceleration if hitting an unprotected zygomatic bone. Problem 82P: 82 ** EST A bottle rocket burns for 1.6s. After it stops burning, it continues moving up to a... Problem 83P: 83. * Data from state driver’s manual The state driver’s manual lists the reaction distances,... Problem 85P: 85. * Car A is heading east at 30 m/s and Car B is heading west at 20 m/s. Suddenly, as they... Problem 86RPP: BIO Head injuries in sports A research group at Dartmouth College has developed a Head Impact... Problem 87RPP: BIO Head injuries in sports A research group at Dartmouth College has developed a Head Impact... Problem 88RPP: BIO Head injuries in sports A research group at Dartmouth College has developed a Head Impact... Problem 89RPP: BIO Head injuries in sports A research group at Dartmouth College has developed a Head Impact... Problem 90RPP: BIO Head injuries in sports A research group at Dartmouth College has developed a Head Impact... Problem 91RPP: Automatic sliding doors The first automatic sliding doors were described by Hero of Alexandria... Problem 92RPP:
Automatic sliding doors The first automatic sliding doors were described by Hero of Alexandria... Problem 93RPP: Automatic sliding doors The first automatic sliding doors were described by Hero of Alexandria... Problem 94RPP: Automatic sliding doors The first automatic sliding doors were described by Hero of Alexandria... Problem 95RPP: Automatic sliding doors The first automatic sliding doors were described by Hero of Alexandria... Problem 96RPP: Automatic sliding doors The first automatic sliding doors were described by Hero of Alexandria... format_list_bulleted


 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning




