Chapter 2, Problem 2.76AP

Astronauts on a distant planet toss a rock into the air. With the aid of a camera that takes pictures at a steady rate, they record the rock’s height as a function of time as given in the following table, (a) Find the rock’s average velocity in the time interval between each measurement and the next, (b) Using these average velocities to approximate instantaneous velocities at the midpoints of the lime intervals, make a graph of velocity as a function of time, (c) Does the rock move with constant acceleration? If so, plot a straight line of best fit on the graph and calculate its slope to find the acceleration.

To determine

The average velocity of rock in the time interval between each measurement and the next.

Answer to Problem 2.76AP

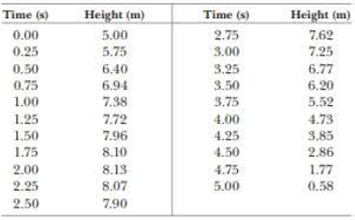
The rock’s height as a function of time is shown in below given table.

Time (s)	Height (m)	Average velocity ( $\text{m}/\text{s}$ )	Midpoint time (s)
$0.00$	$5.00$
$0.25$	$5.75$	$\begin{array}{l}3\hfill \end{array}$	$0.125$
$0.50$	$6.40$	$2.6$	$0.375$
$0.75$	$6.94$	$2.16$	$0.625$
$1.00$	$7.38$	$1.76$	$0.875$
$1.25$	$7.72$	$1.36$	$1.125$
$1.50$	$7.96$	$0.96$	$1.375$
$1.75$	$8.10$	$0.56$	$1.625$
$2.00$	$8.13$	$0.12$	$1.875$
$2.25$	$8.07$	$-0.24$	$2.125$
$2.50$	$7.90$	$-0.68$	$2.375$
$2.75$	$7.62$	$-1.12$	$2.625$
$3.00$	$7.25$	$-1.48$	$2.875$
$3.25$	$6.77$	$-1.92$	$3.125$
$3.50$	$6.20$	$-2.28$	$3.375$
$3.75$	$5.52$	$-2.72$	$3.625$
$4.00$	$4.73$	$-3.16$	$3.875$
$4.25$	$3.85$	$-3.52$	$4.125$
$4.50$	$2.86$	$-3.96$	$4.375$
$4.75$	$1.77$	$-4.36$	$4.625$
$5.00$	$0.58$	$-4.76$	$4.875$

Table (1)

Explanation of Solution

Given info: The rock’s height as a function of time is shown in below given table.

Time (s)	Height (m)
$0.00$	$5.00$
$0.25$	$5.75$
$0.50$	$6.40$
$0.75$	$6.94$
$1.00$	$7.38$
$1.25$	$7.72$
$1.50$	$7.96$
$1.75$	$8.10$
$2.00$	$8.13$
$2.25$	$8.07$
$2.50$	$7.90$
$2.75$	$7.62$
$3.00$	$7.25$
$3.25$	$6.77$
$3.50$	$6.20$
$3.75$	$5.52$
$4.00$	$4.73$
$4.25$	$3.85$
$4.50$	$2.86$
$4.75$	$1.77$
$5.00$	$0.58$

Table (2)

The formula to calculate the average velocity is,

$v_{\text{avg}}=\frac{x_{\text{f}}-x_{\text{i}}}{t}$

Here,

$x_{\text{f}}$ is the final position.

$x_{\text{i}}$ is the initial position.

$t$ is the time interval.

The formula to calculate the midpoint time is,

$t=\frac{t_2-t_1}{2}$

Here,

$t_2$ is the final time.

$t_1$ is the initial time.

Substitute the values given in table (1) and calculate the average velocity and midpoint time as mentioned in the table.

Time (s)	Height (m)	Average velocity ( $\text{m}/\text{s}$ )	Midpoint time (s)
$0.00$	$5.00$
$0.25$	$5.75$	$\begin{array}{l}3\hfill \end{array}$	$0.125$
$0.50$	$6.40$	$2.6$	$0.375$
$0.75$	$6.94$	$2.16$	$0.625$
$1.00$	$7.38$	$1.76$	$0.875$
$1.25$	$7.72$	$1.36$	$1.125$
$1.50$	$7.96$	$0.96$	$1.375$
$1.75$	$8.10$	$0.56$	$1.625$
$2.00$	$8.13$	$0.12$	$1.875$
$2.25$	$8.07$	$-0.24$	$2.125$
$2.50$	$7.90$	$-0.68$	$2.375$
$2.75$	$7.62$	$-1.12$	$2.625$
$3.00$	$7.25$	$-1.48$	$2.875$
$3.25$	$6.77$	$-1.92$	$3.125$
$3.50$	$6.20$	$-2.28$	$3.375$
$3.75$	$5.52$	$-2.72$	$3.625$
$4.00$	$4.73$	$-3.16$	$3.875$
$4.25$	$3.85$	$-3.52$	$4.125$
$4.50$	$2.86$	$-3.96$	$4.375$
$4.75$	$1.77$	$-4.36$	$4.625$
$5.00$	$0.58$	$-4.76$	$4.875$

Table (3)

Conclusion:

Therefore, the rock’s height as a function of time is shown in below given table.

Time (s)	Height (m)	Average velocity ( $\text{m}/\text{s}$ )	Midpoint time (s)
$0.00$	$5.00$
$0.25$	$5.75$	$\begin{array}{l}3\hfill \end{array}$	$0.125$
$0.50$	$6.40$	$2.6$	$0.375$
$0.75$	$6.94$	$2.16$	$0.625$
$1.00$	$7.38$	$1.76$	$0.875$
$1.25$	$7.72$	$1.36$	$1.125$
$1.50$	$7.96$	$0.96$	$1.375$
$1.75$	$8.10$	$0.56$	$1.625$
$2.00$	$8.13$	$0.12$	$1.875$
$2.25$	$8.07$	$-0.24$	$2.125$
$2.50$	$7.90$	$-0.68$	$2.375$
$2.75$	$7.62$	$-1.12$	$2.625$
$3.00$	$7.25$	$-1.48$	$2.875$
$3.25$	$6.77$	$-1.92$	$3.125$
$3.50$	$6.20$	$-2.28$	$3.375$
$3.75$	$5.52$	$-2.72$	$3.625$
$4.00$	$4.73$	$-3.16$	$3.875$
$4.25$	$3.85$	$-3.52$	$4.125$
$4.50$	$2.86$	$-3.96$	$4.375$
$4.75$	$1.77$	$-4.36$	$4.625$
$5.00$	$0.58$	$-4.76$	$4.875$

To determine

To draw: The velocity versus time graph.

Answer to Problem 2.76AP

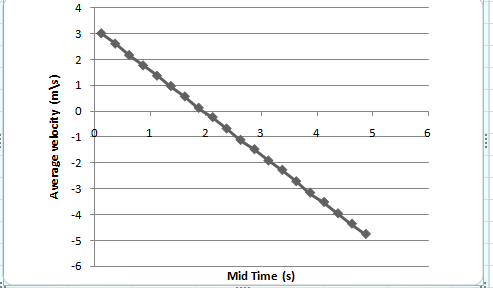
The average velocity versus mid time graph is,

Explanation of Solution

Introduction:

The velocity is defined as rate of change of position of the object. The Midpoint time is the mean of the time interval taken for which position of the object is defined. Plot the difference of the position with respect to midpoint time to obtain velocity time graph.

From part (a) make a graph using values of average velocity and mid time from table (1) as shown below.

Figure (1)

Conclusion:

Therefore, the average velocity versus mid time graph is,

To determine

Whether the rock moves with constant acceleration and determine the acceleration.

Answer to Problem 2.76AP

The rock moves with constant acceleration and the acceleration is $-1.63\text{m}/{\text{s}}^{\text{2}}$.

Explanation of Solution

The formula to calculate speed of rock from its graph in figure (1) is,

$v=mt+c$

Substitute $-1.6339$ for $m$ and $3.2$ for $c$ in the above equation.

$v=-1.6339t+3.2$

Thus the slope of curve is $-1.6339$ and the slope of average velocity to time graph represents its acceleration. As the slope of graph is constant so the rock has constant acceleration.

Hence, the acceleration of rock is $-1.6339\text{m}/{\text{s}}^{\text{2}}$.

Conclusion:

Therefore, the rock moves with constant acceleration and the acceleration is $-1.63\text{m}/{\text{s}}^{\text{2}}$.