EBK PRACTICE OF STATISTICS IN THE LIFE
4th Edition
ISBN: 9781319067496
Author: BALDI
Publisher: VST
expand_more
expand_more
format_list_bulleted
Question
Chapter 2, Problem 2.6AYK
(a)
To determine
To find: the five-number summary of the dataset.
(a)
Expert Solution
Answer to Problem 2.6AYK
| Statistics | Group Instruction | Individual instruction |
| Minimum: | 78 | 128 |
| First | 117.50 | 159.75 |
| 147.50 | 191.50 | |
| Third quartile: | 172.00 | 221.50 |
| Maximum: | 359 | 283 |
Explanation of Solution
Given:
| Group Instruction | 141 | 158 | 112 | 153 | 134 | 95 | 96 | 78 | 148 |
| 172 | 200 | 271 | 103 | 172 | 359 | 145 | 147 | 255 | |
| Individual instruction | 128 | 195 | 188 | 158 | 227 | 198 | 163 | 164 | |
| 159 | 128 | 283 | 226 | 223 | 221 | 220 | 160 |
Calculation:
The five-point statistics calculated using the Excel is given below:
|
| Group Instruction | Individual instruction |
| count | 18 | 16 |
| 163.28 | 190.06 | |
| sample variance | 4,992.21 | 1,755.66 |
| sample standard deviation | 70.66 | 41.90 |
| minimum | 78 | 128 |
| maximum | 359 | 283 |
| 281 | 155 | |
| 1st quartile | 117.50 | 159.75 |
| median | 147.50 | 191.50 |
| 3rd quartile | 172.00 | 221.50 |
| 54.50 | 61.75 | |
| 172.00 | 128.00 | |
The five-point summery is:
| Statistics | Group Instruction | Individual instruction |
| Minimum: | 78 | 128 |
| First quartile: | 117.50 | 159.75 |
| Median: | 147.50 | 191.50 |
| Third quartile: | 172.00 | 221.50 |
| Maximum: | 359 | 283 |
(b)
To determine
To construct: the box plot for the given datasets.
(b)
Expert Solution
Explanation of Solution
Calculation:
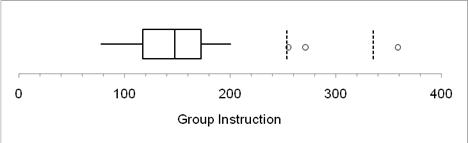
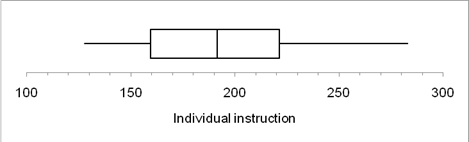
The summery shown by the box plots is given below:
| Statistics | Group Instruction | Individual instruction |
| Minimum: | 78 | 128 |
| First quartile: | 117.50 | 159.75 |
| Median: | 147.50 | 191.50 |
| Third quartile: | 172.00 | 221.50 |
| Maximum: | 359 | 283 |
| low extremes | 0 | 0 |
| low outliers | 0 | 0 |
| high outliers | 2 | 0 |
| high extremes | 1 | 0 |
(c)
To determine
To find: the mean and standard deviation and explain whether it defines anything about shape or not.
(c)
Expert Solution
Answer to Problem 2.6AYK
Group Instruction:
Mean = 163.28
Standard Deviation = 70.66
Individual instruction:
Mean =190.66
Standard Deviation = 41.90
Explanation of Solution
Formula used:
Mean = Average(“Array”)
Standard Deviation = stdev.s(“array”)
Calculation:
| Statistics | Group Instruction | Individual instruction |
| Mean | 163.28 | 190.06 |
| Standard Deviation | 70.66 | 41.90 |
No, mean and standard are the values that tells about the central value and the standard deviation tell about the spread of the data but not the shape of the data.
(d)
To determine
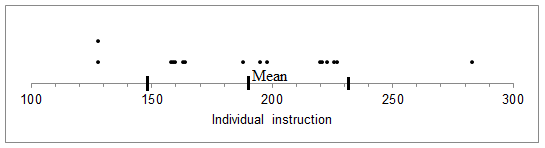
To represent the mean, one standard deviation above and one standard deviation below the mean on the dot plot of the given two datasets.
(d)
Expert Solution
Explanation of Solution
The dot plots showing the mean and one standard deviation below and one standard deviation above than then mean is given below.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
In order to find probability, you can use this formula in Microsoft Excel:
The best way to understand and solve these problems is by first drawing a bell curve and marking key points such as x, the mean, and the areas of interest. Once marked on the bell curve, figure out what calculations are needed to find the area of interest.
=NORM.DIST(x, Mean, Standard Dev., TRUE).
When the question mentions “greater than” you may have to subtract your answer from 1.
When the question mentions “between (two values)”, you need to do separate calculation for both values and then subtract their results to get the answer.
1.
Compute the probability of a value between 44.0 and 55.0.
(The question requires finding probability value between 44 and 55. Solve it in 3 steps.
In the first step, use the above formula and x = 44, calculate probability value.
In the second step repeat the first step with the only difference that x=55.
In the third step, subtract the answer of the first part from the…
If a uniform distribution is defined over the interval from 6 to 10, then answer the followings:
What is the mean of this uniform distribution?
Show that the probability of any value between 6 and 10 is equal to 1.0
Find the probability of a value more than 7.
Find the probability of a value between 7 and 9.
The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be:
More than $27?
Less than or equal to $24?
The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches.
What is the mean amount of rainfall for the month?
What is the probability of less than an inch of rain for the month?
What is the probability of exactly 1.00 inch of rain?
What is the probability of more than 1.50 inches of rain for the month?
The best way to solve this problem is begin by creating a chart. Clearly mark the range, identifying the lower and upper…
Problem 1:
The mean hourly pay of an American Airlines flight attendant is normally distributed with a mean of 40 per hour and a standard deviation of 3.00 per hour. What is the probability that the hourly pay of a randomly selected flight attendant is:
Between the mean and $45 per hour?
More than $45 per hour?
Less than $32 per hour?
Problem 2:
The mean of a normal probability distribution is 400 pounds. The standard deviation is 10 pounds.
What is the area between 415 pounds and the mean of 400 pounds?
What is the area between the mean and 395 pounds?
What is the probability of randomly selecting a value less than 395 pounds?
Problem 3:
In New York State, the mean salary for high school teachers in 2022 was 81,410 with a standard deviation of 9,500. Only Alaska’s mean salary was higher. Assume New York’s state salaries follow a normal distribution.
What percent of New York State high school teachers earn between 70,000 and 75,000?
What percent of New York State high school…
Chapter 2 Solutions
EBK PRACTICE OF STATISTICS IN THE LIFE
Ch. 2 - Prob. 2.1AYKCh. 2 - Prob. 2.2AYKCh. 2 - Prob. 2.3AYKCh. 2 - Prob. 2.4AYKCh. 2 - Prob. 2.5AYKCh. 2 - Prob. 2.6AYKCh. 2 - Prob. 2.7AYKCh. 2 - Prob. 2.8AYKCh. 2 - Prob. 2.9AYKCh. 2 - Prob. 2.10AYK
Ch. 2 - Prob. 2.11AYKCh. 2 - Prob. 2.12AYKCh. 2 - Prob. 2.13AYKCh. 2 - Prob. 2.14CYSCh. 2 - Prob. 2.15CYSCh. 2 - Prob. 2.16CYSCh. 2 - Prob. 2.17CYSCh. 2 - Prob. 2.18CYSCh. 2 - Prob. 2.19CYSCh. 2 - Prob. 2.20CYSCh. 2 - Prob. 2.21CYSCh. 2 - Prob. 2.22CYSCh. 2 - Prob. 2.23CYSCh. 2 - Prob. 2.24ECh. 2 - Prob. 2.26ECh. 2 - Prob. 2.27ECh. 2 - Prob. 2.28ECh. 2 - Prob. 2.29ECh. 2 - Prob. 2.30ECh. 2 - Prob. 2.31ECh. 2 - Prob. 2.32ECh. 2 - Prob. 2.33ECh. 2 - Prob. 2.34ECh. 2 - Prob. 2.35ECh. 2 - Prob. 2.36ECh. 2 - Prob. 2.37ECh. 2 - Prob. 2.38ECh. 2 - Prob. 2.39ECh. 2 - Prob. 2.40ECh. 2 - Prob. 2.41E
Knowledge Booster
Similar questions
- Pls help asaparrow_forwardSolve the following LP problem using the Extreme Point Theorem: Subject to: Maximize Z-6+4y 2+y≤8 2x + y ≤10 2,y20 Solve it using the graphical method. Guidelines for preparation for the teacher's questions: Understand the basics of Linear Programming (LP) 1. Know how to formulate an LP model. 2. Be able to identify decision variables, objective functions, and constraints. Be comfortable with graphical solutions 3. Know how to plot feasible regions and find extreme points. 4. Understand how constraints affect the solution space. Understand the Extreme Point Theorem 5. Know why solutions always occur at extreme points. 6. Be able to explain how optimization changes with different constraints. Think about real-world implications 7. Consider how removing or modifying constraints affects the solution. 8. Be prepared to explain why LP problems are used in business, economics, and operations research.arrow_forwardged the variance for group 1) Different groups of male stalk-eyed flies were raised on different diets: a high nutrient corn diet vs. a low nutrient cotton wool diet. Investigators wanted to see if diet quality influenced eye-stalk length. They obtained the following data: d Diet Sample Mean Eye-stalk Length Variance in Eye-stalk d size, n (mm) Length (mm²) Corn (group 1) 21 2.05 0.0558 Cotton (group 2) 24 1.54 0.0812 =205-1.54-05T a) Construct a 95% confidence interval for the difference in mean eye-stalk length between the two diets (e.g., use group 1 - group 2).arrow_forward
- An article in Business Week discussed the large spread between the federal funds rate and the average credit card rate. The table below is a frequency distribution of the credit card rate charged by the top 100 issuers. Credit Card Rates Credit Card Rate Frequency 18% -23% 19 17% -17.9% 16 16% -16.9% 31 15% -15.9% 26 14% -14.9% Copy Data 8 Step 1 of 2: Calculate the average credit card rate charged by the top 100 issuers based on the frequency distribution. Round your answer to two decimal places.arrow_forwardPlease could you check my answersarrow_forwardLet Y₁, Y2,, Yy be random variables from an Exponential distribution with unknown mean 0. Let Ô be the maximum likelihood estimates for 0. The probability density function of y; is given by P(Yi; 0) = 0, yi≥ 0. The maximum likelihood estimate is given as follows: Select one: = n Σ19 1 Σ19 n-1 Σ19: n² Σ1arrow_forward
- Please could you help me answer parts d and e. Thanksarrow_forwardWhen fitting the model E[Y] = Bo+B1x1,i + B2x2; to a set of n = 25 observations, the following results were obtained using the general linear model notation: and 25 219 10232 551 XTX = 219 10232 3055 133899 133899 6725688, XTY 7361 337051 (XX)-- 0.1132 -0.0044 -0.00008 -0.0044 0.0027 -0.00004 -0.00008 -0.00004 0.00000129, Construct a multiple linear regression model Yin terms of the explanatory variables 1,i, x2,i- a) What is the value of the least squares estimate of the regression coefficient for 1,+? Give your answer correct to 3 decimal places. B1 b) Given that SSR = 5550, and SST=5784. Calculate the value of the MSg correct to 2 decimal places. c) What is the F statistics for this model correct to 2 decimal places?arrow_forwardCalculate the sample mean and sample variance for the following frequency distribution of heart rates for a sample of American adults. If necessary, round to one more decimal place than the largest number of decimal places given in the data. Heart Rates in Beats per Minute Class Frequency 51-58 5 59-66 8 67-74 9 75-82 7 83-90 8arrow_forward
- can someone solvearrow_forwardQUAT6221wA1 Accessibility Mode Immersiv Q.1.2 Match the definition in column X with the correct term in column Y. Two marks will be awarded for each correct answer. (20) COLUMN X Q.1.2.1 COLUMN Y Condenses sample data into a few summary A. Statistics measures Q.1.2.2 The collection of all possible observations that exist for the random variable under study. B. Descriptive statistics Q.1.2.3 Describes a characteristic of a sample. C. Ordinal-scaled data Q.1.2.4 The actual values or outcomes are recorded on a random variable. D. Inferential statistics 0.1.2.5 Categorical data, where the categories have an implied ranking. E. Data Q.1.2.6 A set of mathematically based tools & techniques that transform raw data into F. Statistical modelling information to support effective decision- making. 45 Q Search 28 # 00 8 LO 1 f F10 Prise 11+arrow_forwardStudents - Term 1 - Def X W QUAT6221wA1.docx X C Chat - Learn with Chegg | Cheg X | + w:/r/sites/TertiaryStudents/_layouts/15/Doc.aspx?sourcedoc=%7B2759DFAB-EA5E-4526-9991-9087A973B894% QUAT6221wA1 Accessibility Mode பg Immer The following table indicates the unit prices (in Rands) and quantities of three consumer products to be held in a supermarket warehouse in Lenasia over the time period from April to July 2025. APRIL 2025 JULY 2025 PRODUCT Unit Price (po) Quantity (q0)) Unit Price (p₁) Quantity (q1) Mineral Water R23.70 403 R25.70 423 H&S Shampoo R77.00 922 R79.40 899 Toilet Paper R106.50 725 R104.70 730 The Independent Institute of Education (Pty) Ltd 2025 Q Search L W f Page 7 of 9arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman