Chapter 2, Problem 2.55P

(a)

To determine

The equation of motion of particle and resolve into three components, also show that the motion of the particle remains constant in the plane $z=0$.

Answer to Problem 2.55P

The equation of motion of the charged particle is $\underset{\_}{m{\dot{v}}_x\widehat{i}+m{\dot{v}}_y\widehat{j}+m{\dot{v}}_z\widehat{k}=q\left[B{v}_y\widehat{i}+\left(E-v_{x}B\right)\widehat{j}\right]}$ and the motion of the particle remains constant in the plane $z=0$ since $v_z$ is constant.

Explanation of Solution

Write the expression for force experienced by a particle moving in electric and magnetic field.

    $F=q\left(E+v\times B\right)$

Here, $F$ is the force experienced by the particle, $q$ is the charge of the particle, $E$ is the electric field, $v$ is the velocity, and $B$ is the magnetic field.

The above can also be written as

    $m\dot{v}=q\left(E+v\times B\right)$        (I)

In terms of component along $x$, $y$, and $z$. The above equation is written as

    $\begin{array}{c}m{\dot{v}}_x\widehat{i}+m{\dot{v}}_y\widehat{j}+m{\dot{v}}_z\widehat{k}=q\left[jE+\left(v_x\widehat{i}+v_y\widehat{j}+v_z\widehat{k}\right)\times \left(\widehat{k}B\right)\right]\\ m{\dot{v}}_x\widehat{i}+m{\dot{v}}_y\widehat{j}+m{\dot{v}}_z\widehat{k}=q\left[B{v}_y\widehat{i}+\left(E-v_{x}B\right)\widehat{j}\right]\end{array}$        (II)

Equate the components along $x$ direction.

    $\begin{array}{c}m{\dot{v}}_x=qB{v}_y\\ {\dot{v}}_x=\frac{qB{v}_y}{m}\end{array}$

Since $\frac{qB}{m}=\omega$, the above equation is written as

    ${\dot{v}}_x=\omega v_y$        (III)

Equate the components along $y$ direction.

    $\begin{array}{c}m{\dot{v}}_y=q\left(E-B{v}_x\right)\\ {\dot{v}}_y=-\frac{qB}{m}\left(v_x-\frac{E}{B}\right)\end{array}$

Since $\frac{qB}{m}=\omega$, the above equation is written as

    ${\dot{v}}_y=-\omega \left(v_x-\frac{E}{B}\right)$        (IV)

Equate the components along $z$ direction.

    ${\dot{v}}_z=0$        (V)

From the above equation it is clear that $v_z$ is constant. Thus the particle remains in the $z$ plane.

Conclusion:

Therefore, the equation of motion of the charged particle is $\underset{\_}{m{\dot{v}}_x\widehat{i}+m{\dot{v}}_y\widehat{j}+m{\dot{v}}_z\widehat{k}=q\left[B{v}_y\widehat{i}+\left(E-v_{x}B\right)\widehat{j}\right]}$ and the motion of the particle remains constant in the plane $z=0$ since $v_z$ is constant.

(b)

To determine

To show that for a unique value of $v_{x0}$, for which the particle moves undeflected through the fields.

Answer to Problem 2.55P

As $E$ and $B$ are constant, $v_{dr}$ takes an unique value for which the particle moves undeflected through the fields.

Explanation of Solution

Let the initial speed of the particle for which the particle remains undeflected is $v_{dr}$. Thus $v_{xo}=v_{dr}$.

Write the expression for electrostatic force on the particle.

    $F_{\text{E}}=Eq$        (VI)

Here, $F_{\text{E}}$ is the electrostatic force, $E$ is the electric field, and $q$ is the charge of the particle.

Write the expression for magnetic force.

    $F_{\text{B}}=Bq{v}_{xo}$

Here, $F_{\text{B}}$ is the magnetic force, $B$ is the magnetic field, $q$ is the charge, and $v_{xo}$ is the initial velocity of the particle.

Since the initial speed of the particle is equal to the drift speed of the particle, the above equation is reduced to

    $F_{\text{B}}=Bq{v}_{dr}$        (VII)

For a particle to be undeflected, the magnitude of electrostatic force and magnetic force should be equal.

Using the above condition, equate equation (VI) and (VII).

    $Eq=Bq{v}_{dr}$

Rearrange the above equation.

    $v_{dr}=\frac{E}{B}$

As $E$ and $B$ are constant, $v_{dr}$ takes unique value.

Conclusion:

Therefore, as $E$ and $B$ are constant, $v_{dr}$ takes an unique value for which the particle moves undeflected through the fields.

(c)

To determine

To solve the equation of motion of the particle, and to obtain the velocity of as a function of $t$.

Answer to Problem 2.55P

The velocity of the particle as a function of $t$ is given by $\underset{\_}{v_x=v_{dr}+\left(v_{xo}-v_{dr}\right)\cos \omega t}$, $\underset{\_}{v_y=-\left(v_{xo}-v_{dr}\right)\sin \omega t}$, and $\underset{\_}{v_z=0}$.

Explanation of Solution

The speed of the particle along $x$ direction is given by

    $v_x=u_x+v_{dr}$        (VIII)

Differentiating the above equation with respect to time.

    ${\dot{v}}_x={\dot{u}}_x$

The above equation can also be written as

    ${\dot{u}}_x=\omega u_y$

The solution of the above equation is given by

    $u_x=A\cos \omega t$        (IX)

Given that the speed of the particle along $y$ direction.

    $v_y=u_y$        (X)

Differentiating the above equation with respect to time.

    ${\dot{v}}_y={\dot{u}}_y$

The above equation is written as

    ${\dot{u}}_y=-\omega u_x$

The solution of the above equation is given by

    $u_y=-A\sin \omega t$

Since $u_y$ is equal to $v_y$, the above equation is written as

$v_y=-A\sin \omega t$        (XI)

Use equation (IX) in equation (VIII).

    $v_x=A\cos \omega t+v_{dr}$        (XII)

At time $t=0$ $v_x$ is taken as $v_{xo}$, thus the above equation is written as

    $\begin{array}{c}{v}_{xo}=A\cos \omega \left(0\right)+v_{dr}\\ v_{xo}-v_{dr}=A\cos \left(0\right)\\ A=v_{xo}-v_{dr}\end{array}$        (XIII)

Use the above equation in equation (XII).

    $v_x=\left(v_{xo}-v_{dr}\right)\cos \omega t+v_{dr}$        (XIV)

Use equation (XIII) in equation (XI).

    $v_y=-\left(v_{xo}-v_{dr}\right)\sin \omega t$        (XV)

And speed along $z$ direction is zero $v_z=0$.

Conclusion:

Therefore, the velocity of the particle as a function of $t$ is given by $\underset{\_}{v_x=v_{dr}+\left(v_{xo}-v_{dr}\right)\cos \omega t}$, $\underset{\_}{v_y=-\left(v_{xo}-v_{dr}\right)\sin \omega t}$, and $\underset{\_}{v_z=0}$.

(d)

To determine

The position of the particle as a function of time $t$, and to sketch the trajectory for various values of $v_{xo}$.

Answer to Problem 2.55P

The position of the particle as a function of time $t$ is $\underset{\_}{x=v_{dr}t+R\sin \omega t}$, and $\underset{\_}{y=R\left(\cos \omega t-1\right)}$, the trajectories of the particle is plotted in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, and Figure 7.

Explanation of Solution

From subpart (c), $v_y$ is given by

    $v_y=-\left(v_{xo}-v_{dr}\right)\sin \omega t$

The above equation is written as

    $\begin{array}{c}\frac{dy}{dt}=-\left(v_{xo}-v_{dr}\right)\sin \omega t\\ dy=-\left(v_{xo}-v_{dr}\right)\sin \omega tdt\end{array}$        (XVI)

Replace $dy$ as $d{y}^{\prime }$, $t$ as $t^{\prime }$, and $dt$ as $d{t}^{\prime }$ in the above equation, and integrate $d{y}^{\prime }$ from $0\text{to }y$, and $d{t}^{\prime }$ from $0\text{to}t$.

    $\begin{array}{c}{\displaystyle {\int }_0^{y}d{y}^{\prime }}={\displaystyle {\int }_0^t-\left(v_{xo}-v_{dr}\right)\sin \omega t^{\prime }d{t}^{\prime }}\\ {\left(y^{\prime }\right)}_0^y={\left[-\left(v_{xo}-v_{dr}\right)\left(\frac{-\cos \omega t^{\prime }}{\omega }\right)\right]}_0^t\\ y-0=\frac{v_{xo}-v_{dr}}{\omega }[\cos \omega t-\cos \omega (0)]\\ y=R\left[\cos \omega t-1\right]\end{array}$        (XVI)

Similarly position $x$ is obtained as

    $x=v_{dr}t+R\sin \omega t$        (XVII)

Assuming $v_{xo}$ is in multiples of $v_{dr}$ and $v_{xo}=n{v}_{dr}$, then $R$ is given by

    $\begin{array}{c}R=\frac{n{v}_{dr}-v_{dr}}{\omega }\\ =\left(n-1\right)\frac{v_{dr}}{\omega }\end{array}$        (XVIII)

Use the above equation in equation (XVII).

    $x=v_{dr}t+\left(n-1\right)\frac{v_{dr}}{\omega }\sin \omega t$

Use equation (XIV) in equation (XVI).

    $y=\left(n-1\right)\frac{v_{dr}}{\omega }\left[\cos \omega t-1\right]$

For $v_{dr}=1$ and $\omega =1$ position $x$ is given by

    $x=t+\left(n-1\right)\sin t$

For $v_{dr}=1$ and $\omega =1$ position $y$ is given by

    $y=\left(n-1\right)\left(\cos t-1\right)$

Figure 1 represents the trajectory of $v_{xo}=3$.

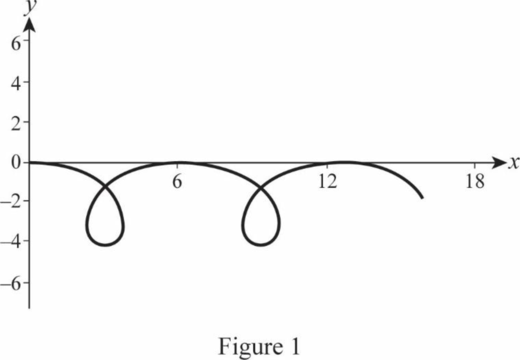
Figure 2 represents the trajectory of $v_{xo}=2$.

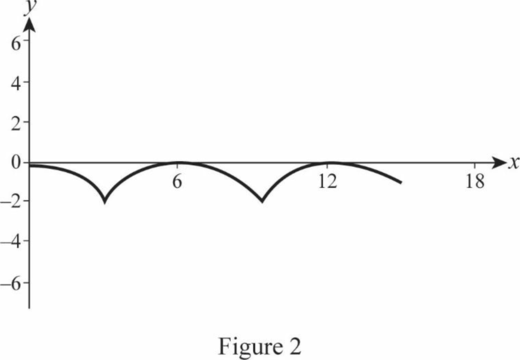
Figure 3 represents the trajectory of $v_{xo}=1.5$.

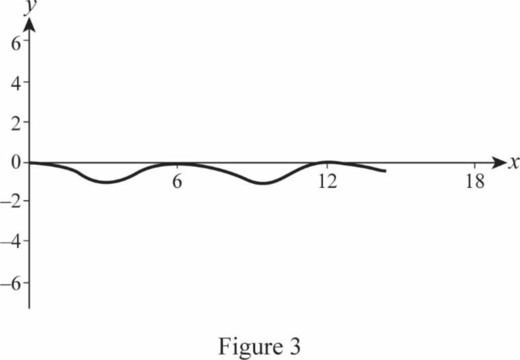
Figure 4 represents the trajectory of $v_{xo}=1$.

Figure 5 represents the trajectory of $v_{xo}=0.5$.

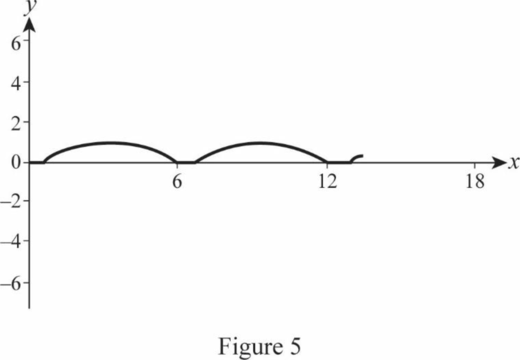
Figure 6 represents the trajectory of $v_{xo}=0$.

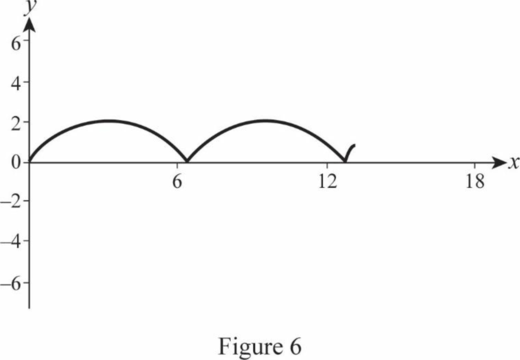
Figure 7 represents the trajectory of $v_{xo}=-1$.

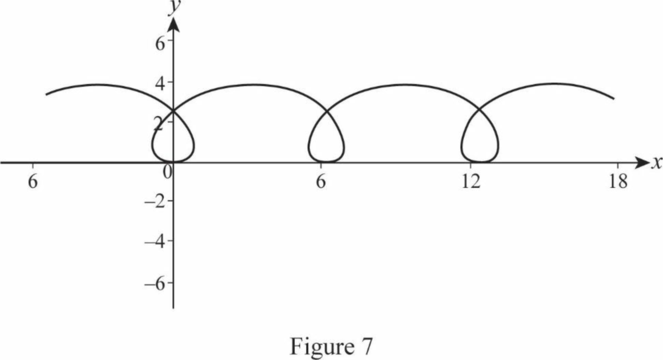
Conclusion:

Therefore, the position of the particle as a function of time $t$ is $\underset{\_}{x=v_{dr}t+R\sin \omega t}$, and $\underset{\_}{y=R\left(\cos \omega t-1\right)}$, the trajectories of the particle is plotted in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, and Figure 7.