
Concept explainers
A wind power system with increasing windspeed has the current waveform described by the equation below, delivered to an 80 Ω resistor. Plot the current, power, and energy waveform over a period of 60 s, and calculate the total energy collected over the 60 s time period.
Sketch the current, power, and energy waveform over a period of 60 s to the current waveform of the wind power system. Also calculate the total energy collected over the 60 s time period.
Answer to Problem 22E
The plot for the current, power, and energy waveform is sketched as shown in Figure 1, and the total energy collected over the 60 s time period is
Explanation of Solution
Given data:
The current waveform is,
The resistor is
Formula used:
Write the general expression to find the power as follows,
Write the general expression to find the energy as follows,
Calculation:
Substitute the value of
Applying equation (3) in equation (2) as follows,
Consider the function,
Consider
Substituting the values in equation (5) as follows,
Consider,
Applying the product to sum formulas in the above expression as follows,
Consider,
By applying integration by parts in the above expression,
Applying the values in equation (8) as follows,
Consider the function,
Solving,
By applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Solving,
By applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Solving,
By applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying the values in the above expression,
Substituting the values in equation (13) as follows,
Substitute the above value in the considered expression
Substitute the above value in equation (12) as follows,
Substitute the above value in equation (11) as follows,
Substitute the above value in equation (10) as follows,
Substitute the above value in equation (9) as follows,
Consider the function
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Substituting the values,
Substitute the above value in equation (22) as follows,
Substitute the above value in equation (21) as follows,
Substitute the above value in equation (20) as follows,
Substitute the above value in equation (18) as follows
Substitute the above value in equation (17) as follows
Substitute the above value in equation (16) as follows
Substitute the above value in equation (15) as follows
Consider the function
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying integration by parts in the above expression,
Applying the values in the above equation as follows,
Consider,
Let,
Applying the values in the above equation as follows,
Substitute the above value in equation (33) as follows,
Substitute the above value in equation (31) as follows,
Substitute the above value in equation (30) as follows,
Substitute the above value in equation (29) as follows,
Substitute the above value in equation (28) as follows,
Substitute the above value in equation (26) as follows,
Substitute the above value in equation (25) as follows,
Consider the function
Substitute the calculated values of equation (34), (35), (23), and (14) in the expression x as follows,
Substitute the above value in equation (6) as follows,
Substitute
Applying the limits to the above expression over a period of 60 s,
Matlab code to plot for wind power waveform:
t_end = 60; % End time in seconds
t_pts = 600; % Number of points for time vector
t=linspace(0,t_end,t_pts); % Define time vector
dt=t_end/t_pts; % Separation between time points
R=80; % Resistance in ohms
for i=1:t_pts; % Iterate for each point in time
current(i)=0.5*t(i)^2*sin(pi/8*t(i))*cos(pi/4*t(i));
p(i)=current(i)^2*R;
end
w=cumsum(p)*dt; % Energy from cumulative sum times time separation
figure(1)
subplot(3,1,1); plot(t,current,'r'); % Plot voltage
ylabel('Current (A)');
subplot(3,1,2); plot(t,p,'r') % Plot power
ylabel('Power (W)')
subplot(3,1,3); plot(t,w,'r') % Plot energy
xlabel('Time (seconds)')
ylabel('Energy (J)')
Matlab output:
Figure 1 shows the plot for the current, power, and energy waveform.
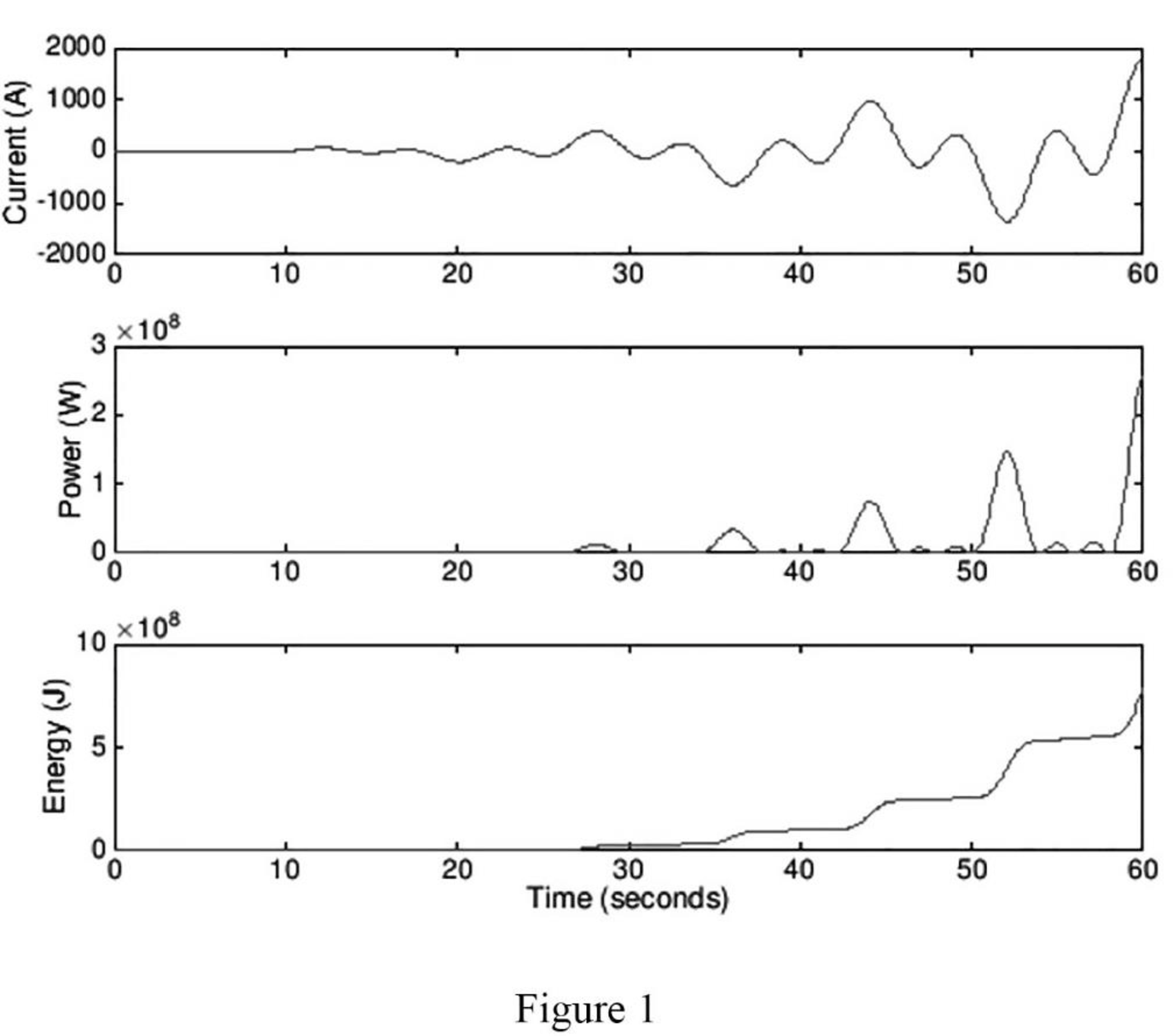
Conclusion:
Thus, the plot for the current, power, and energy waveform is sketched as shown in Figure 1, and the total energy collected over the 60 s time period is
Want to see more full solutions like this?
Chapter 2 Solutions
Engineering Circuit Analysis
- I need an expert mathematical solution. The radiation intensity of an aperture antenna, mounted on an infinite ground plane with perpendicular to the aperture. is rotationally symmetric (not a function of 4), and it is given by sin (7 sin 0) U π sin Find the approximate directivity (dimensionless and in dB) usingarrow_forwardWaveforms v1(t) and v2(t) are given by:v1(t) = −4 sin(6π ×10^4t +30◦) V,v2(t) = 2cos(6π ×10^4t −30◦) V.Does v2(t) lead or lag v1(t), and by what phase angle?arrow_forward7.1 Express the current waveform i(t) = -0.2 cos(6 × 10°1 +60°) mA in standard cosine form and then determine the following: (a) Its amplitude, frequency, and phase angle. (b) i(t) at t=0.1 ns.arrow_forward
- 3. Consider the RC circuit with a constant voltage source shown in the diagram below. The values of the resistor, capacitor, and input voltage are R = 50, C = 10 µF, and V = 6V, respectively. Assume that there is initially no charge on the capacitor before the switch is closed. Vo ↑i(t) R w C When the switch closes at time t = 0, the current begins to flow as a function of time according to the equation i(t) = ioencarrow_forwardQ2. a) A three-phase 415 V, 4-pole, 50 Hz, A-connected induction motor was tested. The obtained results are: (i) (ii) No load test 50 Hz: Blocked rotor test, 10 Hz: DC test: Vnl=415 V, Pnl=1200 W, In=11 A Vbr 10 V, Pbr=1500 W, Ibr=91 A VDC 3 V, IDC=107 A Draw the per-phase equivalent electrical circuit of the motor Draw the circuits for no-load and block-rotor tests and indicate the slip for each of the tests. (iii) Identify the motor parameters (iv) Calculate the motor's starting torque at the rated voltage.arrow_forward4. Consider the RC circuit with a sinusoid voltage source shown in the diagram below. The values of the resistor, capacitor, input voltage amplitude and frequency are R-20012, C-5pF", Vo-10V, and w=500 rad/s, respectively. Assume that the circuit has reached steady state. Vрейте 2 The input voltage can be described using the complex sinusoid function V(t)-Vo and the physical voltage is obtained by taking the real part of V(t). The voltage drop across the capacitor is given by a sinusoid with same the frequency was the input voltage, but a different magnitude and different phase. In complex form, the capacitor's voltage is given by Vc(t)=1+jwRC For the following questions, use the template file Assignment TemplateQ2.m as the starting point for your MATLAB code. (a) (6 marks) Use MATLAB to make a graph that shows the real part of the input voltage source ReV(t)] and the real part of the voltage drop across the capacitor Re[Ve(t)] as a function of time. Choose the time scale so that two…arrow_forward
- Consider the microgrid given in figure 8-56. The positive sequence impedance of the transmission Lines is given in -line diagram (figure 8.5%). The system data are as follows: the one PV generating Station: 2MW, 460V. AC, positive, negative and zero Sequence impedance of each line is equal to 10%. The generator negativ Sequence impedance is equal to the positive Sequence, and the Zero Sequence impedance is equal to half (½) of positiv Sequence impedance. Transformers positive sequence impedance is equal to the negative sequence and equal to the zero sequence impedance Station DC/AC CB Acpu bus CB www S+js 5 1+jlo M 2 T2 SB CB A Jus -3+16 local utilityarrow_forwarda) The current drawn by a single-phase converter is represented by the waveform in the figure below. Use Fourier series analysis to determine an expression for obtaining the rms values of the fundamental and the harmonics of the source current. Hence, express the rms value of the fundamental as well as the first three harmonics of the waveform. i(t) Id - Id π 元 b) Fig. Input current waveform of a single phase bridge rectifier A sinusoidal voltage with a peak value of 300 V is applied to the converter in (a) drawing a square-wave current with a peak value of 15 A. Assuming that the zero crossing of the current waveform is 45° behind that of the input voltage waveform, calculate: (i) the average power drawn by the converter, (ii) the form factor (FF) and ripple factor (RF) (iii) the total harmonic distortion (THD%) of the input current.arrow_forwardTransformer 600 V Transformer L₁ L₂ L3 4 (a) 600 V L₁ L₂ L3 L₁ (b) Figure 3.arrow_forward
- (2 marks) Using Kirchoff's voltage law: V(t) = VR(t) + Vc(t), show that the voltage drop across the resistor is given by the equation VR(t) jwRC 1+jwRC Voearrow_forwardA ferrite ETD44 core type material is to be used in the converter design. If Bmax = 0.52T, and 350 turns of 1.5x10³cm² copper wire is to be wound around the core material to allow a flow of 5A maximum current, compute for the (a) inductor resistance, and the (b) inductance.arrow_forwardDon't use ai to answer I will report you answerarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





