
Concept explainers
Reduce each of the networks shown in Figure P2.1 to a single equivalent resistance by combining resistances in series and parallel.
* Denotes that answers are contained in the Student Solutions flies. See Appendix E for more information about accessing the Student Solutions
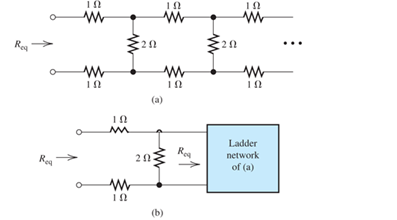
FIgure P2.1
(a)
The equivalent resistance by combining resistance in series.
Answer to Problem 2.1P
The value of equivalent resistance is
Explanation of Solution
Calculation:
The required diagram is shown in Figure 1.
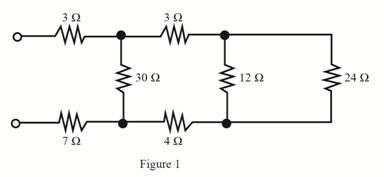
Mark the resistance
The required diagram is shown in Figure 2.
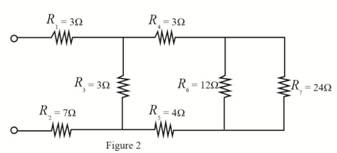
The value of resistance
Substitute
The required diagram is shown in Figure 3.
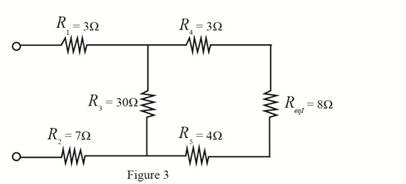
The value of resistance
Substitute
The required diagram is shown in Figure 4.
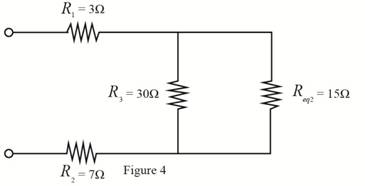
The value of resistance
Substitute
The required diagram is shown in Figure 5.
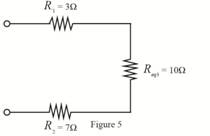
The value of resistance
Substitute
The required diagram is shown in Figure 6.
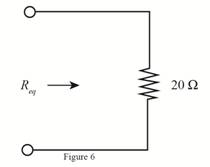
Conclusion:
Therefore, the value of equivalent resistance is
(b)
The equivalent resistance by combining resistance in series.
Answer to Problem 2.1P
The value of equivalent resistance is
Explanation of Solution
Calculation:
The required diagram is shown in Figure 7.

The value of resistance
Substitute
The required diagram is shown in Figure 8.
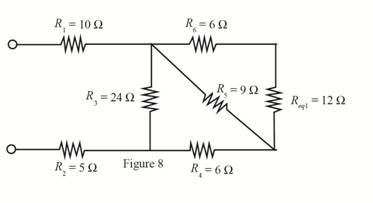
The value of resistance
Substitute
The equivalent resistance is shown in Figure 9.
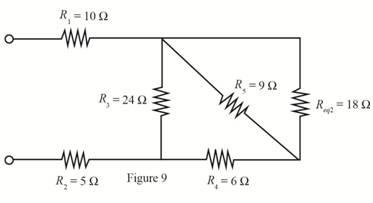
The value of resistance
Substitute
The required diagram is shown in Figure 10.
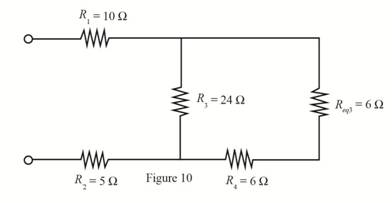
The value of resistance
Substitute
The equivalent resistance is shown in Figure 11.
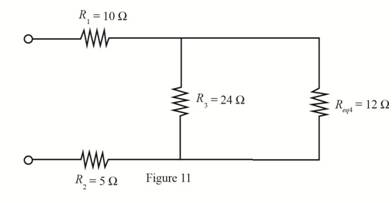
The value of resistance
Substitute
The required diagram is shown in Figure 12.
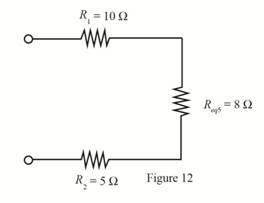
The value of resistance
Substitute
The required diagram is shown in Figure 13.
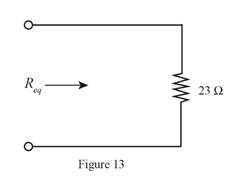
Conclusion:
Therefore, the value of equivalent resistance is
Want to see more full solutions like this?
Chapter 2 Solutions
Electrical Engineering: Principles & Applications Plus Mastering Engineering with Pearson eText -- Access Card Package (7th Edition)
- I need an expert mathematical solution. The radiation intensity of an aperture antenna, mounted on an infinite ground plane with perpendicular to the aperture. is rotationally symmetric (not a function of 4), and it is given by U sin (77 sin 0) π sin Find the approximate directivity (dimensionless and in dB) using numerical integration. Use the DIRECTIVITY computer program at the end of this chapter.arrow_forwardDon't use ai to answer I will report you answer.arrow_forwardDon't use ai to answer I will report you answerarrow_forward
- Need handwritten solution not using chatgptarrow_forwardHandwritten Solution pleasearrow_forwardThe E-field pattern of an antenna. independent of , varies as follows: E 0 0° ≤ 0≤ 45° 45°<≤ 90° 90° <8180° (a) What is the directivity of this antenna? Umax 7 why did we use this law Umax = 12 but we divided by 2? In the sent Solution = R 27arrow_forward
- The normalized far-zone field pattern of an antenna is given by (sin cos²) E = 0 00 and 0 ≤ ≤ π/2. 3/22 π elsewhere Find the directivity using (a) the exact expression In the sent soalation Use Prad=2+1 7/2 Pre= 2 + 1 Sco³odo + 5 siño de Where did the 2 Com from?arrow_forwardPen and paper solution please with explaination not using chatgptarrow_forwardhowarrow_forward
- A four pole generator having wave wound armature winding has 51 slots ,each slot containing 20 conductors,what will be the voltage generated in the machine when driven at 1500rpm assuming the flux per pole is 7mWb Don't use Artificial intelligencearrow_forwardNeed Handwritten solution Do not use chatgpt Or AIarrow_forwardI need a detailed solution to a problem. The far-zone electric field intensity (array factor) of an end-fire two-element array antenna, placed along the z-axis and radiating into free-space, is given by E=cos (cos - 1) Find the directivity using (a) Kraus' approximate formula (b) the DIRECTIVITY computer program at the end of this chapter Repeat Problem 2.19 when E = cos -jkr 0505π $[ (cos + 1) (a). Elmax = Cost (case-1)] | max" = 1 at 8-0°. 0.707 Emax = 0.707.(1) = cos [(cose,-1)] (cose-1) = ± 0,= {Cos' (2) = does not exist (105(0)= 90° = rad. Bir Do≈ 4T ar=2() = = Bar 4-1-273 = 1.049 dB T₂ a. Elmax = cos((cose +1)), 0.707 = cos (Close,+1)) = 1 at 6 = π Imax (Cose+1)=== G₁ = cos(-2) does not exist. Girar=2()=π. 4T \cos (0) + 90° + rad Do≈ = +=1.273=1.049dB IT 2arrow_forward
 Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
