LINEAR ALGEBRA+ITS APPLICATIONS-TEXT
6th Edition
ISBN: 9780135851029
Author: Lay
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 1.9, Problem 36E
In Exercises 25-28, determine if the specified linear transformation is (a) one-to-one and (b) onto. Justify each answer.
28. The transformation in Exercise 14
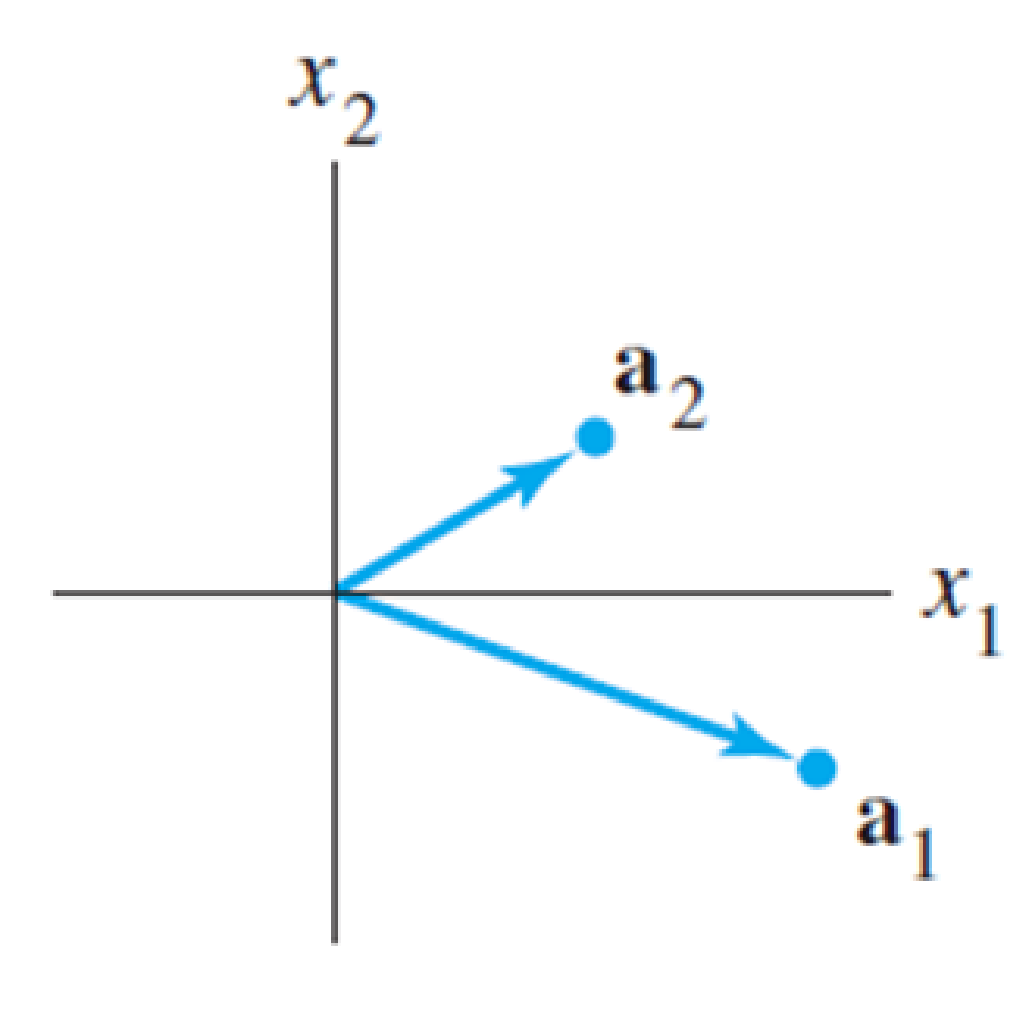
14. Let T : ℝ2 → ℝ2 be a linear transformation with standard matrix A = [a1 a2], where a1 and a2 are shown in the figure. Using the figure, draw the image of
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Which rule describes the transformation b
Determine whether the function L: P2 → P2 defined by L(a0 +a1x+a2x2) = a1 +2a2xis a linear transformation. Explain, and show all your work.
I really need help with
Chapter 1 Solutions
LINEAR ALGEBRA+ITS APPLICATIONS-TEXT
Ch. 1.1 - State in words the next elementary row operation...Ch. 1.1 - The augmented matrix of a linear system has been...Ch. 1.1 - Is (3, 4, 2) a solution of the following system?...Ch. 1.1 - For what values of h and k is the following system...Ch. 1.1 - Solve each system in Exercises 1-4 by using...Ch. 1.1 - Solve each system in Exercises 1-4 by using...Ch. 1.1 - Find the point (x1, x2) that lies on the line x1 +...Ch. 1.1 - Find the point of intersection of the lines x1 ...Ch. 1.1 - Consider each matrix in Exercises 5 and 6 as the...Ch. 1.1 - Consider each matrix in Exercises 5 and 6 as the...
Ch. 1.1 - In Exercises 7-10, the augmented matrix of a...Ch. 1.1 - In Exercises 7—10, the augmented matrix of a...Ch. 1.1 - In Exercises 7-10, the augmented matrix of a...Ch. 1.1 - In Exercises 7—10, the augmented matrix of a...Ch. 1.1 - Solve the systems in Exercises 11—14. 11....Ch. 1.1 - Solve the systems in Exercises 11-14. 12....Ch. 1.1 - Solve the systems in Exercises 11-14. 13....Ch. 1.1 - Solve the systems in Exercises 11-14....Ch. 1.1 - Verify that the solution you found to Exercise 11...Ch. 1.1 - Verify that the solution you found to Exercise 12...Ch. 1.1 - Verify that the solution you found to Exercise 13...Ch. 1.1 - Verify that the solution you found to Exercise 14...Ch. 1.1 - Determine if the systems in Exercises 15 and 16...Ch. 1.1 - Determine if the systems in Exercises 15 and 16...Ch. 1.1 - Do the three lines x1 4x2 = 1, 2x1 x2 = 3, and...Ch. 1.1 - Do the three planes x1 + 2x2 + x3 = 4, x2 x3 = 1,...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - In Exercises 27—34, key statements from this...Ch. 1.1 - Find an equation involving g, h, and k that makes...Ch. 1.1 - Construct three different augmented matrices for...Ch. 1.1 - Suppose the system below is consistent for all...Ch. 1.1 - Suppose a, b, c, and d are constants such that a...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - An important concern in the study of heat transfer...Ch. 1.1 - Solve the system of equations from Exercise 43....Ch. 1.2 - Find the general solution of the linear system...Ch. 1.2 - Find the general solution of the system...Ch. 1.2 - Suppose a 4 7 coefficient matrix for a system of...Ch. 1.2 - In Exercises 1 and 2, determine which matrices are...Ch. 1.2 - In Exercises 1 and 2, determine which matrices are...Ch. 1.2 - Row reduce the matrices in Exercises 3 and 4 to...Ch. 1.2 - Row reduce the matrices in Exercises 3 and 4 to...Ch. 1.2 - Describe the possible echelon forms of a nonzero 2...Ch. 1.2 - Repeat Exercise 5 for a nonzero 3 2 matrix. 5....Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - You may find it helpful to review the information...Ch. 1.2 - You may find it helpful to review the information...Ch. 1.2 - You may find it helpful to review the information...Ch. 1.2 - You may find it helpful to review the information...Ch. 1.2 - Exercises 15 and 16 use the notation of Example 1...Ch. 1.2 - Exercises 15 and 16 use the notation of Example 1...Ch. 1.2 - In Exercises 17 and 18, determine the value(s) of...Ch. 1.2 - In Exercises 17 and 18, determine the value(s) of...Ch. 1.2 - In Exercises 19 and 20, choose h and k such that...Ch. 1.2 - In Exercises 19 and 20, choose h and k such that...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - Prob. 33ECh. 1.2 - In Exercises 25—34, mark each statement True or...Ch. 1.2 - Suppose a 3 5 coefficient matrix for a system has...Ch. 1.2 - Suppose a system of linear equations has a 3 5...Ch. 1.2 - Suppose the coefficient matrix of a system of...Ch. 1.2 - Suppose the coefficient matrix of a linear system...Ch. 1.2 - Restate the last sentence in Theorem 2 using the...Ch. 1.2 - What would you have to know about the pivot...Ch. 1.2 - A system of linear equations with fewer equations...Ch. 1.2 - Give an example of an inconsistent underdetermined...Ch. 1.2 - A system of linear equations with more equations...Ch. 1.2 - Suppose an n (n + 1) matrix is row reduced to...Ch. 1.2 - Find the interpolating polynomial p(t) = a0 + a1t...Ch. 1.2 - [M] In a wind tunnel experiment, die force on a...Ch. 1.3 - Prob. 1PPCh. 1.3 - For what value(s) of h will y be in Span{v1, v2,...Ch. 1.3 - Prob. 3PPCh. 1.3 - In Exercises 1 and 2, compute u+v and u2v. 1....Ch. 1.3 - In Exercises 1 and 2, compute u+v and u2v. 1....Ch. 1.3 - In Exercises 3 and 4, display the following...Ch. 1.3 - In Exercises 3 and 4, display the following...Ch. 1.3 - In Exercises 5 and 6, write a system of equations...Ch. 1.3 - In Exercises 5 and 6, write a system of equations...Ch. 1.3 - Use the accompanying figure to write each vector...Ch. 1.3 - Use the accompanying figure to write each vector...Ch. 1.3 - In Exercises 9 and 10, write a vector equation...Ch. 1.3 - In Exercises 9 and 10, write a vector equation...Ch. 1.3 - In Exercises 11 and 12, determine if b is a linear...Ch. 1.3 - In Exercises 11 and 12, determine if b is a linear...Ch. 1.3 - In Exercises 13 and 14, determine if b is a linear...Ch. 1.3 - In Exercises 13 and 14, determine if b is a linear...Ch. 1.3 - In Exercises 15 and 16, list five vectors in Span...Ch. 1.3 - In Exercises 15 and 16, list five vectors in Span...Ch. 1.3 - Let a1=[142],a2=[237],andb=[41h]. For what...Ch. 1.3 - Let v1=[102],v2=[318],andy=[h53]. For what...Ch. 1.3 - Give a geometric description of Span {v1, v2} for...Ch. 1.3 - Give a geometric description of Span {v1, v2} for...Ch. 1.3 - Let u=[21]andv=[21]. Show that [hk] is an Span {u,...Ch. 1.3 - Construct a 3 3 matrix A, with nonzero entries,...Ch. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - In Exercises 23—32, mark each statement True or...Ch. 1.3 - In Exercises 23—32, mark each statement True or...Ch. 1.3 - Prob. 27ECh. 1.3 - In Exercises 23—32, mark each statement True or...Ch. 1.3 - In Exercises 23—32, mark each statement True or...Ch. 1.3 - Let A = [104032263] and b = [414]. Denote the...Ch. 1.3 - Let A = [206185121], let b = [1033], let W be the...Ch. 1.3 - A mining company has two mines. One days operation...Ch. 1.3 - A steam plain bums two types of coal: anthracite...Ch. 1.3 - Let v1, vk be points in 3 and suppose that for j...Ch. 1.3 - A thin triangular plate of uniform density and...Ch. 1.3 - Consider the vectors v1, v2, v3, and b in 2, shown...Ch. 1.3 - Use the vectors u = (u1, , un), v = (v1, , vn),...Ch. 1.3 - Use the vector u = (u1, , un) to verify the...Ch. 1.4 - Let A = [152031954817], P = [3204], and b = [790]....Ch. 1.4 - Let A = [2531], u = [41], and v = [35]. Verify...Ch. 1.4 - Construct a 3 3 matrix A and vectors b and c in 3...Ch. 1.4 - Compute the products in Exercises 1-4 using (a)...Ch. 1.4 - Compute the products in Exercises 1—4 using (a)...Ch. 1.4 - Compute the products in Exercises 1-4 using (a)...Ch. 1.4 - Compute the products in Exercises 1—4 using (a)...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 9 and 10, write the system first as a...Ch. 1.4 - In Exercises 9 and 10, write the system first as a...Ch. 1.4 - Given A and b in Exercises 11 and 12, write the...Ch. 1.4 - Given A and b in Exercises 11 and 12, write the...Ch. 1.4 - Let u=044 and A=352611. Is u in the plane in R3...Ch. 1.4 - Let u = [232] and A = [587011130]. Is u in the...Ch. 1.4 - Let A = [2163] and b = [b1b2]. Show that the...Ch. 1.4 - Repeat Exercise 15: A = [134326518], b = [b1b2b3]....Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Let v1 = [1010], v2 = [0101], v3 = [1001]. Does...Ch. 1.4 - Let v1 = [002], v2 = [038], v3 = [415]. Does {v1,...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - In Exercises 23—34, mark each statement True or...Ch. 1.4 - Note that [431525623][312]=[7310]. Use this fact...Ch. 1.4 - Let u = [725], v = [313], and w = [610]. It can be...Ch. 1.4 - Let q1, q2, q3, and v represent vectors in 5, and...Ch. 1.4 - Rewrite the (numerical) matrix equation below in...Ch. 1.4 - Construct a 3 3 matrix, not in echelon form,...Ch. 1.4 - Construct a 3 3 matrix, not in echelon form,...Ch. 1.4 - Let A be a 3 2 matrix. Explain why the equation...Ch. 1.4 - Could a set of three vectors in 4 span all of 4?...Ch. 1.4 - Suppose A is a 4 3 matrix and b is a vector in 4...Ch. 1.4 - Suppose A is a 3 3 matrix and b is a vector in 3...Ch. 1.4 - Let A be a 3 4 matrix, let y1 and y2 be vectors...Ch. 1.4 - Let A be a 5 3 matrix, let y be a vector in 3,...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - Prob. 52ECh. 1.5 - Each of the following equations determines a plane...Ch. 1.5 - Write the general solution of 10x1 3x2 2x3 = 7...Ch. 1.5 - Prove the first pan of Theorem 6: Suppose that p...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 5 and 6, follow the method of...Ch. 1.5 - In Exercises 5 and 6, follow the method of...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - Prob. 13ECh. 1.5 - You may find it helpful to review the information...Ch. 1.5 - Suppose the solution set of a certain system of...Ch. 1.5 - Suppose the solution set of a certain system of...Ch. 1.5 - Follow the method of Example 3 to describe the...Ch. 1.5 - As in Exercise 19, describe the solutions of the...Ch. 1.5 - Describe and compare the solution sets of x1 + 9x2...Ch. 1.5 - Describe and compare the solution sets of x1 3x2...Ch. 1.5 - In Exercises 19 and 20, find the parametric...Ch. 1.5 - In Exercises 19 and 20, find the parametric...Ch. 1.5 - In Exercises 21 and 22, find a parametric equation...Ch. 1.5 - In Exercises 21 and 22, find a parametric equation...Ch. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - Prob. 32ECh. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - Prob. 34ECh. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - In Exercises 27—36, mark each statement True or...Ch. 1.5 - Prove the second part of Theorem 6: Let w be any...Ch. 1.5 - Suppose Ax = b has a solution. Explain why the...Ch. 1.5 - Suppose A is the 3 3 zero matrix (with all zero...Ch. 1.5 - If b 0, can the solution set of Ax = b be a plane...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - Given A = [2672139], find one nontrivial solution...Ch. 1.5 - Given A = [4681269], find one nontrivial solution...Ch. 1.5 - Construct a 3 3 nonzero matrix A such that the...Ch. 1.5 - Construct a 3 3 nonzero matrix A such that the...Ch. 1.5 - Construct a 2 2 matrix A such that the solution...Ch. 1.5 - Suppose A is a 3 3 matrix and y is a vector in 3...Ch. 1.5 - Let A be an m n matrix and let u be a vector in n...Ch. 1.5 - Let A be an m n matrix, and let u and v be...Ch. 1.6 - Suppose an economy has three sectors: Agriculture,...Ch. 1.6 - Consider the network flow studied in Example 2....Ch. 1.6 - Suppose an economy has only two sectors, Goods and...Ch. 1.6 - Find another set of equilibrium prices for the...Ch. 1.6 - Boron sulfide reacts violently with water to form...Ch. 1.6 - When solutions of sodium phosphate and barium...Ch. 1.6 - Alka-Seltzer contains sodium bicarbonate (NaHCO3)...Ch. 1.6 - The following reaction between potassium...Ch. 1.6 - Prob. 9ECh. 1.6 - Find the general flow pattern of the network shown...Ch. 1.6 - a. Find the general traffic pattern in the freeway...Ch. 1.6 - a. Find the general flow pattern in the network...Ch. 1.6 - Intersections in England are often constructed as...Ch. 1.7 - Let u = [324] , v = [617] , w = [052] , and z =...Ch. 1.7 - Suppose that {v1, v2, v3} is a linearly dependent...Ch. 1.7 - In Exercises 1—4, determine if the vectors are...Ch. 1.7 - In Exercises 1-4, determine if the vectors are...Ch. 1.7 - In Exercises 1—4, determine if the vectors are...Ch. 1.7 - In Exercises 1-4, determine if the vectors are...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 9 and 10, (a) for what values of h is...Ch. 1.7 - In Exercises 9 and 10, (a) for what values of h is...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - In Exercises 21—28, mark each statement True or...Ch. 1.7 - Prob. 22ECh. 1.7 - In Exercises 21—28, mark each statement True or...Ch. 1.7 - In Exercises 21—28, mark each statement True or...Ch. 1.7 - In Exercises 21—28, mark each statement True or...Ch. 1.7 - Prob. 26ECh. 1.7 - In Exercises 21—28, mark each statement True or...Ch. 1.7 - In Exercises 21—28, mark each statement True or...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - How many pivot columns must a 7 5 matrix have if...Ch. 1.7 - How many pivot columns must a 5 7 matrix have if...Ch. 1.7 - Construct 3 2 matrices A and B such that Ax = 0...Ch. 1.7 - a. Fill in the blank in the following statement:...Ch. 1.7 - Exercises 31 and 32 should be solved without...Ch. 1.7 - Exercises 31 and 32 should be solved without...Ch. 1.7 - Each statement in Exercises 39—44 is either true...Ch. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Each statement in Exercises 39—44 is either true...Ch. 1.7 - Each statement in Exercises 39—44 is either true...Ch. 1.7 - Prob. 44ECh. 1.7 - Suppose A is an m n matrix with the property that...Ch. 1.7 - Suppose an m n matrix A has n pivot columns....Ch. 1.7 - [M] In Exercises 41 and 42, use as many columns of...Ch. 1.7 - [M] In Exercises 41 and 42, use as many columns of...Ch. 1.8 - Suppose T : 5 2 and T(x) = Ax for some matrix A...Ch. 1.8 - A=[1001] Give a geometric description of the...Ch. 1.8 - The line segment from 0 to a vector u is the set...Ch. 1.8 - Let A=[2002], and define T : 22 by T(x) = Ax. Find...Ch. 1.8 - Let A=[.5000.5000.5], u=[104], and v=[abc]. Define...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - Let A be a 6 5 matrix. What must a and b be in...Ch. 1.8 - How many rows and columns must a matrix A have in...Ch. 1.8 - For Exercises 9 and 10, find all x in 4 that are...Ch. 1.8 - For Exercises 9 and 10, find all x in 4 that are...Ch. 1.8 - Let b=[110], and let A be the matrix in Exercise...Ch. 1.8 - Let b=[1314]. and let A be the matrix in Exercise...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - Let T : 2 2 be a linear transformation that maps...Ch. 1.8 - The figure shows vectors u, v, and w, along with...Ch. 1.8 - Let e1=[10], e2=[01], y1=[25], and y2=[16], and...Ch. 1.8 - Let x=[x1x2], v1=[25], and v2=[73], and let T : 2 ...Ch. 1.8 - In Exercises 21—30, mark each statement True or...Ch. 1.8 - In Exercises 21—30, mark each statement True or...Ch. 1.8 - Prob. 23ECh. 1.8 - Prob. 24ECh. 1.8 - Prob. 25ECh. 1.8 - In Exercises 21—30, mark each statement True or...Ch. 1.8 - Prob. 27ECh. 1.8 - Prob. 28ECh. 1.8 - In Exercises 21—30, mark each statement True or...Ch. 1.8 - Prob. 30ECh. 1.8 - Let T : 2 2 be the linear transformation that...Ch. 1.8 - Suppose vectors v1, . . . , vp span n, and let T :...Ch. 1.8 - Prob. 33ECh. 1.8 - Let u and v be linearly independent vectors in 3,...Ch. 1.8 - Prob. 35ECh. 1.8 - Let u and v be vectors in n. It can be shown that...Ch. 1.8 - Define f : by f(x) = mx + b. a. Show that f is...Ch. 1.8 - An affine transformation T : n m has the form...Ch. 1.8 - Let T : n m be a linear transformation, and let...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - [M] In Exercises 37 and 38, the given matrix...Ch. 1.8 - [M] In Exercises 37 and 38, the given matrix...Ch. 1.8 - Prob. 47ECh. 1.8 - Prob. 48ECh. 1.9 - Let T : 2 2 be the transformation that first...Ch. 1.9 - Suppose A is a 7 5 matrix with 5 pivots. Let T(x)...Ch. 1.9 - In Exercises 1—10, assume that T is a linear...Ch. 1.9 - In Exercises 1—10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - A linear transformation T : 2 2 first reflects...Ch. 1.9 - Show that the transformation in Exercise 8 is...Ch. 1.9 - Let T : 2 be the linear transformation such that...Ch. 1.9 - Let T : 2 2 be a linear transformation with...Ch. 1.9 - In Exercises 15 and 16 fill in the missing entries...Ch. 1.9 - In Exercises 15 and 16 fill in the missing entries...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - Let T : 2 2 be a linear transformation such that...Ch. 1.9 - Let T : 2 3 be a linear transformation such that...Ch. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - Prob. 26ECh. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - Prob. 28ECh. 1.9 - Prob. 29ECh. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - In Exercises 23—32, mark each statement True or...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 29 and 30, describe the possible...Ch. 1.9 - In Exercises 29 and 30, describe the possible...Ch. 1.9 - Let T : n m be a linear transformation, with A...Ch. 1.9 - Let T : n m be a linear transformation, with A...Ch. 1.9 - Verify the uniqueness of A in Theorem 10. Let T :...Ch. 1.9 - Why is the question Is the linear transformation T...Ch. 1.9 - If a linear transformation T : n m maps n onto m,...Ch. 1.9 - Let S : p n and T : n m be linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.10 - Find a matrix A and vectors x and b such that the...Ch. 1.10 - The container of a breakfast cereal usually lists...Ch. 1.10 - One serving of Post Shredded Wheat supplies 160...Ch. 1.10 - After taking a nutrition class, a big Annies Mac...Ch. 1.10 - The Cambridge Diet supplies .8 g of calcium per...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - Prob. 9ECh. 1.10 - Prob. 10ECh. 1.10 - Prob. 11ECh. 1.10 - [M] Budget Rent A Car in Wichita. Kansas, has a...Ch. 1.10 - [M] Let M and xo be as in Example 3. a. Compute...Ch. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Prob. 4SECh. 1 - Prob. 5SECh. 1 - Prob. 6SECh. 1 - Prob. 7SECh. 1 - Prob. 8SECh. 1 - Prob. 9SECh. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Prob. 11SECh. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Prob. 13SECh. 1 - Prob. 14SECh. 1 - Prob. 15SECh. 1 - Prob. 16SECh. 1 - Prob. 17SECh. 1 - Prob. 18SECh. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Prob. 20SECh. 1 - Mark each statement True or False (T/F). Justify...Ch. 1 - Prob. 22SECh. 1 - Prob. 23SECh. 1 - Prob. 24SECh. 1 - Prob. 25SECh. 1 - Let a and b represent real numbers. Describe the...Ch. 1 - The solutions (x, y, Z) of a single linear...Ch. 1 - Suppose the coefficient matrix of a linear system...Ch. 1 - Determine h and k such that the solution set of...Ch. 1 - Consider the problem of determining whether the...Ch. 1 - Consider the problem of determining whether the...Ch. 1 - Describe the possible echelon forms of the matrix...Ch. 1 - Prob. 33SECh. 1 - Let a1, a2 and b be the vectors in 2 shown in the...Ch. 1 - Construct a 2 3 matrix A, not in echelon form,...Ch. 1 - Construct a 2 3 matrix A, not in echelon form,...Ch. 1 - Write the reduced echelon form of a 3 3 matrix A...Ch. 1 - Determine the value(s) of a such that...Ch. 1 - In (a) and (b), suppose the vectors are linearly...Ch. 1 - Use Theorem 7 in Section 1.7 to explain why the...Ch. 1 - Explain why a set {v1, v2, v3, v4} in 5 must be...Ch. 1 - Suppose {v1, v2} is a linearly independent set in...Ch. 1 - Suppose v1, v2, v3 are distinct points on one line...Ch. 1 - Let T : n m be a linear transformation, and...Ch. 1 - Let T : 3 3 be the linear transformation that...Ch. 1 - Let A be a 3 3 matrix with the property that the...Ch. 1 - A Givens rotation is a linear transformation from...Ch. 1 - The following equation describes a Givens rotation...Ch. 1 - A large apartment building is to be built using...
Additional Math Textbook Solutions
Find more solutions based on key concepts
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Read about basic ideas of statistics in Common Core Standards for grades 3-5, and discuss why students at these...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Therecipe to make 214 times the original amount.
Pre-Algebra Student Edition
In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...
Elementary Statistics (13th Edition)
Sketch the graph of y= x . (p. 22)
Precalculus
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Let T be a linear transformation from R2 into R2 such that T(4,2)=(2,2) and T(3,3)=(3,3). Find T(7,2).arrow_forwardIn Exercises 3-6, prove that the given transformation is a linear transformation, using the definition (or the Remark following Example 3.55). 6.arrow_forwardFor the linear transformation from Exercise 38, find a T(0,1,0,1,0), and b the preimage of (0,0,0), c the preimage of (1,1,2). Linear Transformation Given by a Matrix In Exercises 33-38, define the linear transformation T:RnRmby T(v)=Av. Find the dimensions of Rnand Rm. A=[020201010112221]arrow_forward
- Let T be a linear transformation T such that T(v)=kv for v in Rn. Find the standard matrix for T.arrow_forwardUse the standard matrix for counterclockwise rotation in R2 to rotate the triangle with vertices (3,5), (5,3) and (3,0) counterclockwise 90 about the origin. Graph the triangles.arrow_forward1. Let Ta : ℝ2 → ℝ2 be the matrix transformation corresponding to . Find , where and .arrow_forward
- Find the kernel of the linear transformation T:R4R4, T(x1,x2,x3,x4)=(x1x2,x2x1,0,x3+x4).arrow_forwardFor the linear transformation from Exercise 33, find a T(1,1), b the preimage of (1,1), and c the preimage of (0,0). Linear Transformation Given by a Matrix In Exercises 33-38, define the linear transformations T:RnRm by T(v)=Av. Find the dimensions of Rn andRm. A=[0110]arrow_forwardFor the linear transformation from Exercise 37, find a T(1,0,2,3), and b the preimage of (0,0,0). Linear Transformation Given by a Matrix In Exercises 33-38, define the linear transformations T:RnRm by T(v)=Av. Find the dimensions of Rn and Rm. A=[012114500131]arrow_forward
- Let T:P2P3 be the linear transformation T(p)=xp. Find the matrix for T relative to the bases B={1,x,x2} and B={1,x,x2,x3}.arrow_forwardLet T:RnRm be the linear transformation defined by T(v)=Av, where A=[30100302]. Find the dimensions of Rn and Rm.arrow_forwardLet T:P2P4 be the linear transformation T(p)=x2p. Find the matrix for T relative to the bases B={1,x,x2} and B={1,x,x2,x3,x4}.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Transformations on Vector Spaces; Author: Professor Dave Explains;https://www.youtube.com/watch?v=is1cg5yhdds;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY