
(a)
Consumption and saving.
(a)
Explanation of Solution
According to the life-cycle model of consumption, the consumption of an individual depends on the income earned in the entire life time of an individual.
The total life time income of the individuals can be calculated as the sum of income they earn in different periods using Equation (1) as follows:
Given that A enjoys $100,000 in three periods and F enjoys $40,000 in period1, $100,000 in period2, and $160,000 in period3, both individuals consume for 5 periods in life.
The life-time income of A can be calculated by substituting the respective values in Equation (1) as follows:
Thus, the life-time income of A is $300,000.
The life-time income of F can be calculated by substituting the respective values in Equation (1) as follows:
Thus, the life-time income of F is $300,000.
The life-time consumption of individuals can be calculated using Equation (2) as follows:
The life-time consumption of A can be calculated by substituting the respective values in Equation (2) as follows:
The life-time consumption of A is $60,000.
The life-time consumption of F can be calculated by substituting the respective values in Equation (2) as follows:
The life-time consumption of F is $60,000.
The savings can be calculated as the part of income, which is not consumed. The savings can be calculated using Equation (3) as follows:
The saving in period 1 for A can be calculated by substituting the respective value in Equation (3) as follows:
Thus, A’ savings for period 1 is $40,000.
Table 1 shows the values of savings for A and F in different periods calculated using Equations 1, 2, and 3.
Table 1
| A | F | |
| S1 | 40,000 | -20,000 |
| S2 | 40,000 | 40,000 |
| S3 | 40,000 | 100,000 |
| S4 | -60,000 | -60,000 |
| S5 | -60,000 | -60,000 |
Life-cycle theory: Life-cycle theory developed by Franco Modigliani and Richard Brumberg relates the spending and saving habits of an individual to the course of their life time.
Savings: Savings is defined as that part of income that is not consumed in the current period and is to be used for future consumption.
(b)
The wealth of individuals.
(b)
Explanation of Solution
The wealth of an individual is calculated as the accumulated saving in each period.
The wealth can be calculated using Equation (4) as follows:
The wealth of individual A in the beginning of period 2 is calculated by substituting the respective values in Equation (4) as follows:
Thus, the wealth of A in the beginning of period 2 is $40,000.
Table 2 shows the values of wealth for A and F in different periods, which are calculated using Equation 4.
Table 1
| A | F | |
| W1 | 0 | 0 |
| W2 | 40,000 | -20,000 |
| W3 | 80,000 | 20,000 |
| W4 | 120,000 | 120,000 |
| W5 | 60,000 | 60,000 |
| W6 | 0 | 0 |
It is evident from the table values that there is no wealth in period1 and period 6.
(c)
The graphical representation of consumption, income, and wealth of the individuals.
(c)
Explanation of Solution
Figure 1 given below shows the consumption, income, and wealth of A.
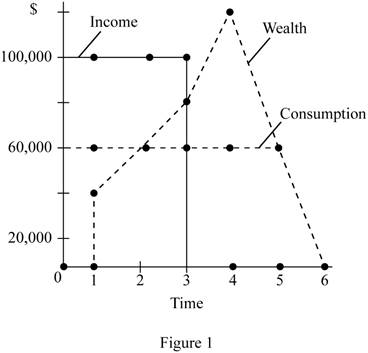
The horizontal axis of Figure 1 measures the time period, and the vertical axis measures the consumption, income, and wealth. A enjoys a fixed income over the first 3 periods, and hence he also has a constant pattern of consumption as clearly depicted in Figure 1. A saves a part of his income and thus gradually increases his wealth during his earning years and gradually dissaves when he leads his retirement life. His pattern of consumption, income, and wealth is according to the prediction of the life-cycle model.
Figure 2 given below shows the consumption, income, and wealth of F.
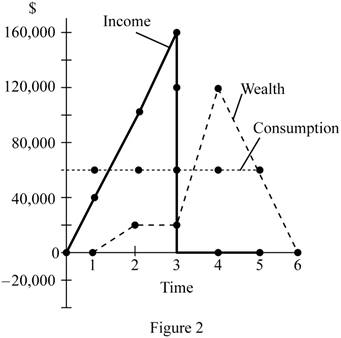
The horizontal axis of Figure 1 measures the time period, and the vertical axis measures the consumption, income, and wealth. F increases his income gradually, and this would force him to borrow initially to enjoy a smooth consumption. When his income increases, he would accumulate wealth and then use it for his consumption in the retirement life.
Savings: Savings is defined as that part of income that is not consumed in the current period and is to be used for future consumption.
Dissaving: The act of spending more than earned in the current period or spending the past savings is known as dissaving.
(d)
The impact of borrowing.
(d)
Explanation of Solution
A has fixed income from the initial years of earning, and hence there is no need for him to borrow. Thus, A’s consumption or income will not be affected when there is a borrowing constraint. However, F depends on borrowing for his initial period. When there is a borrowing constraint, F has to spend his entire income of $40,000 in the initial period. For the later periods, he smooths his consumption by dividing the lifetime income across the remaining periods.
The life-time income of F can be calculated by substituting the respective values in Equation (1) as follows:
Thus, the life-time income of F is $260,000.
The life-time consumption of F can be calculated by substituting the respective values in Equation (2) as follows:
The life-time consumption of F is $65,000.
The saving in period 2 for F can be calculated by substituting the respective values in Equation (3) as follows:
Thus, F’s savings for period 2 is $35,000.
The wealth of individual F in the beginning of period 2 is calculated by substituting the respective values in Equation (4) as follows:
Thus, the wealth of A in the beginning of period 2 is $40,000.
Table 2 shows the values of savings and wealth F in different periods, which are calculated using Equations 3 and 4.
Table 1
| Period | F's Consumption | F's Savings | F's Wealth |
| 0 | 0 | 0 | 0 |
| 1 | 40,000 | 0 | 0 |
| 2 | 65,000 | 35,000 | 35,000 |
| 3 | 65,000 | 95,000 | 130,000 |
| 4 | 65,000 | -65,000 | 65,000 |
| 5 | 65,000 | -65,000 | 0 |
Figure 3 given below shows the consumption, income, and wealth of F.
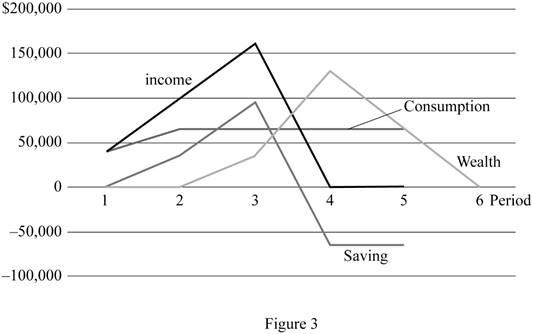
The horizontal axis of Figure 1 measures the time period, and the vertical axis measures the consumption, income, and wealth. F increases his income gradually. However, he faces borrowing constraints, and hence he can only use his initial income for consumption. When his income increases, he would accumulate wealth, and then use it for his consumption in the retirement life.
Savings: Savings is defined as that part of income that is not consumed in the current period and is to be used for future consumption.
Dissaving: The act of spending more than earned in the current period or spending the past savings is known as dissaving.
Want to see more full solutions like this?
- Price P 1. Explain the distinction between outputs and outcomes in social service delivery 2. Discuss the Rawlsian theory of justice and briefly comment on its relevance to the political economy of South Africa. [2] [7] 3. Redistributive expenditure can take the form of direct cash transfers (grants) and/or in- kind subsidies. With references to the graphs below, discuss the merits of these two transfer types in the presence and absence of a positive externality. [6] 9 Quantity (a) P, MC, MB MSB MPB+MEB MPB P-MC MEB Quantity (6) MCarrow_forwardDon't use ai to answer I will report you answerarrow_forwardIf 17 Ps are needed and no on-hand inventory exists fot any of thr items, how many Cs will be needed?arrow_forward
- Exercise 5Consider the demand and supply functions for the notebooks market.QD=10,000−100pQS=900pa. Make a table with the corresponding supply and demand schedule.b. Draw the corresponding graph.c. Is it possible to find the price and quantity of equilibrium with the graph method? d. Find the price and quantity of equilibrium by solving the system of equations.arrow_forward1. Consider the market supply curve which passes through the intercept and from which the marketequilibrium data is known, this is, the price and quantity of equilibrium PE=50 and QE=2000.a. Considering those two points, find the equation of the supply. b. Draw a graph for this equation. 2. Considering the previous supply line, determine if the following demand function corresponds to themarket demand equilibrium stated above. QD=.3000-2p.arrow_forwardSupply and demand functions show different relationship between the price and quantities suppliedand demanded. Explain the reason for that relation and provide one reference with your answer.arrow_forward
- 13:53 APP 簸洛瞭對照 Vo 56 5G 48% 48% atheva.cc/index/index/index.html The Most Trusted, Secure, Fast, Reliable Cryptocurrency Exchange Get started with the easiest and most secure platform to buy, sell, trade, and earn Cryptocurrency Balance:0.00 Recharge Withdraw Message About us BTC/USDT ETH/USDT EOS/USDT 83241.12 1841.50 83241.12 +1.00% +0.08% +1.00% Operating norms Symbol Latest price 24hFluctuation B BTC/USDT 83241.12 +1.00% ETH/USDT 1841.50 +0.08% B BTC/USD illı 83241.12 +1.00% Home Markets Trade Record Mine О <arrow_forwardThe production function of a firm is described by the following equation Q=10,000L-3L2 where Lstands for the units of labour.a) Draw a graph for this equation. Use the quantity produced in the y-axis, and the units of labour inthe x-axis. b) What is the maximum production level? c) How many units of labour are needed at that point?arrow_forwardDon't use ai to answer I will report you answerarrow_forward



 Macroeconomics: Private and Public Choice (MindTa...EconomicsISBN:9781305506756Author:James D. Gwartney, Richard L. Stroup, Russell S. Sobel, David A. MacphersonPublisher:Cengage Learning
Macroeconomics: Private and Public Choice (MindTa...EconomicsISBN:9781305506756Author:James D. Gwartney, Richard L. Stroup, Russell S. Sobel, David A. MacphersonPublisher:Cengage Learning Economics: Private and Public Choice (MindTap Cou...EconomicsISBN:9781305506725Author:James D. Gwartney, Richard L. Stroup, Russell S. Sobel, David A. MacphersonPublisher:Cengage Learning
Economics: Private and Public Choice (MindTap Cou...EconomicsISBN:9781305506725Author:James D. Gwartney, Richard L. Stroup, Russell S. Sobel, David A. MacphersonPublisher:Cengage Learning





