Chapter 19, Problem 19.1P

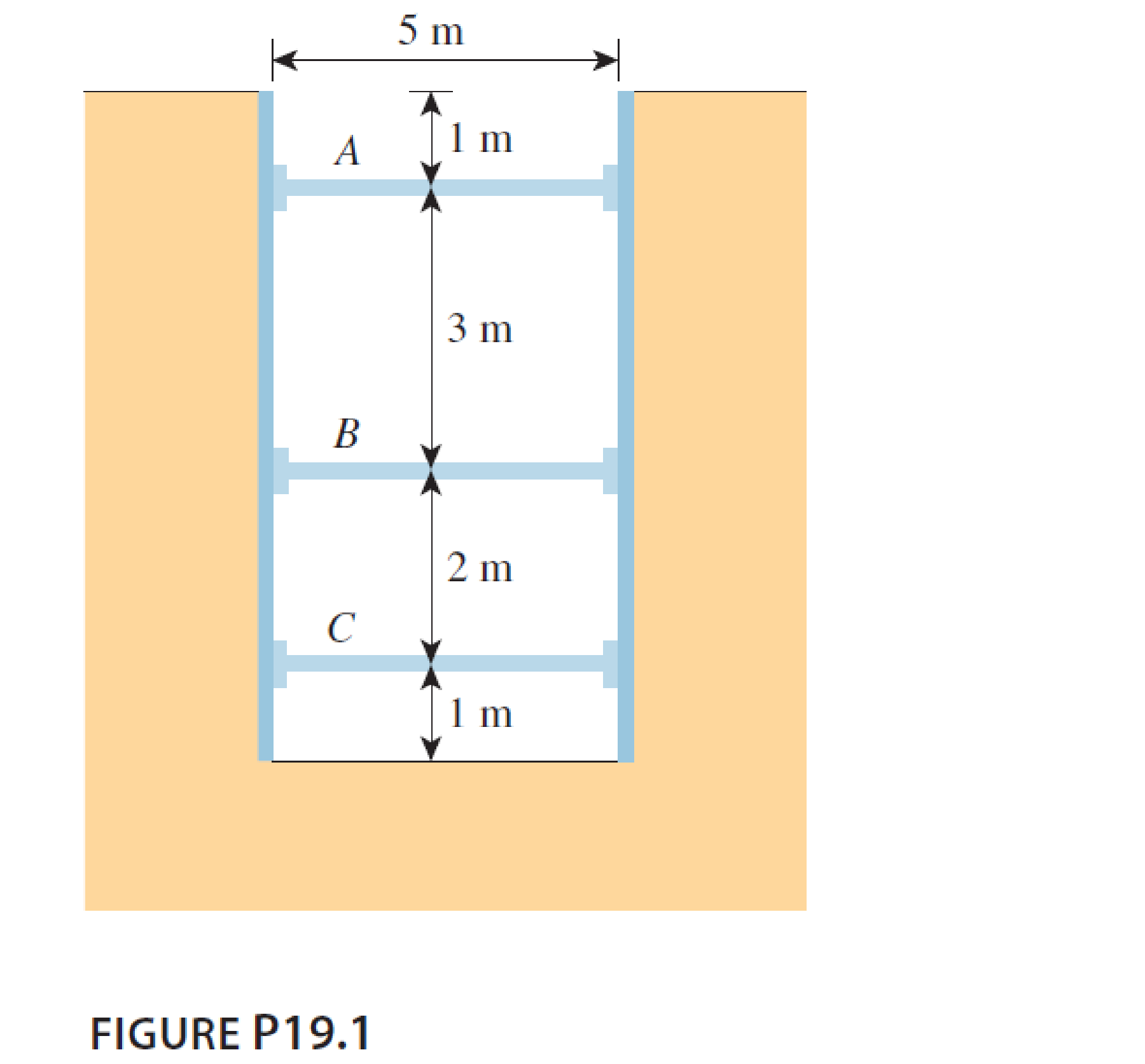
A 5 m wide braced excavation is made in a saturated clay, as shown in Figure P19.1, with the following properties: c = 20 kN/m², ϕ = 0, and γ = 18.5 kN/m³. The struts are spaced at 5 m center to center in plan.

1. a. Determine the strut forces.
2. b. Determine the section modulus of the sheet pile required, assuming σ_all = 170 MN/m².
3. c. Determine the maximum moment for the wales at levels B and C.

To determine

Find the strut force.

Answer to Problem 19.1P

The strut load at A, B, C is $\underset{¯}{\text{413}\text{.4}\text{kN}}$, $\underset{¯}{\text{545}\text{.7}\text{kN}}$, $\underset{¯}{\text{556}\text{.9}\text{kN}}$ respectively.

Explanation of Solution

Given information:

The width of excavation is 5 m.

The height of excavation cut H is 7 m.

The unit weight of saturated clay $\gamma$ is $18.5{\text{kN/m}}^{\text{3}}$.

The coefficient of internal friction $\varphi$ is $0$.

The cohesion (c) is $20{\text{kN/m}}^2$.

The center to center spacing of strut s is 5 m.

Calculation:

Check the condition for soft to medium clay as follows:

$\begin{array}{l}\frac{\gamma H}{c}>4\\ \frac{18.5{\text{kN/m}}^{\text{3}}\times 7\text{m}}{20{\text{kN/m}}^{\text{2}}}>4\\ 6.475>4\end{array}$

Hence, the clay is considered as soft to medium clay.

Find the maximum lateral pressure using the formula.

$\begin{array}{c}{\sigma }_a=\gamma H-4c\\ =\left(18.5\times 7\right)-\left(4\times 20\right)\\ =49.5{\text{kN/m}}^{\text{2}}\end{array}$

$\begin{array}{c}{\sigma }_a=0.3\gamma H\\ =0.3\times 18.5\times 7\\ =38.85{\text{kN/m}}^{\text{2}}\end{array}$

The maximum lateral pressure is $49.5{\text{kN/m}}^{\text{2}}$

Step-1:

Indicate the struts are labeled as A, B, and C and its carrying load as $P_A$, $P_B$, and $P_C$.

Draw the pressure diagram as shown in Figure.

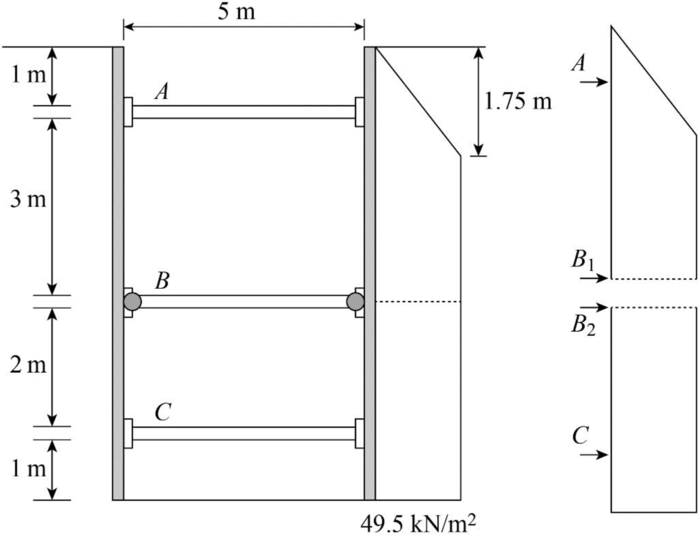
The strut sheet pile connection at B is assumed to be hinge.

Find the strut load per meter width of excavation as follows:

At the top block,

$\Sigma M{B}_1=0$

$\begin{array}{c}\left(A\times 3\right)={\sigma }_a\left(2.25\right)\left(\frac{2.25}{2}\right)+\left(\frac{1}{2}\times {\sigma }_a\times 1.75\times \left(2.25+\frac{1.75}{3}\right)\right)\\ =\left(49.5\right)\left(2.25\right)\left(\frac{2.25}{2}\right)+\left(\frac{1}{2}\times 49.5\times 1.75\times \left(2.25+\frac{1.75}{3}\right)\right)\\ A=82.67\text{kN/m}\end{array}$

$\begin{array}{c}{B}_1=\left({\sigma }_a\times 2.25\right)+\left(\frac{1}{2}\times {\sigma }_a\times 1.75\right)-A\\ =\left(49.5\times 2.25\right)+\left(\frac{1}{2}\times 49.5\times 1.75\right)-82.67\text{kN/m}\\ =72.02\text{kN/m}\end{array}$

For the bottom block,

$\begin{array}{c}\left(C\times 2\right)=\left({\sigma }_a\times 3\times 1.5\right)\\ =\left(49.5\times 3\times 1.5\right)\\ C=111.38\text{kN/m}\end{array}$

$\begin{array}{c}\left(C+B_2\right)=\left({\sigma }_a\times 3\right)\\ 111.38+B_2=\left(49.5\times 3\right)\\ B_2=37.12\text{kN/m}\end{array}$

Find the strut force at A $\left(P_A\right)$

$\begin{array}{c}{P}_A=As\\ =82.67\text{kN/m}\times \text{5}\text{m}\\ =\text{413}\text{.4}\text{kN}\end{array}$

Find the strut load at B $\left(P_B\right)$

$\begin{array}{c}{P}_B=Bs\\ =\left(B_1+B_2\right)s\\ =\left(72.02\text{kN/m}+37.12\text{kN/m}\right)\times \text{5}\text{m}\\ =\text{545}\text{.7}\text{kN}\end{array}$

Find the strut load at C $\left(P_C\right)$

$\begin{array}{c}{P}_C=Cs\\ =111.38\times \text{5}\text{m}\\ =\text{556}\text{.9}\text{kN}\end{array}$

Therefore, The strut load at A, B, C is $\underset{¯}{\text{413}\text{.4}\text{kN}}$, $\underset{¯}{\text{545}\text{.7}\text{kN}}$, $\underset{¯}{\text{556}\text{.9}\text{kN}}$ respectively.

To determine

Find the required section modulus for sheet pile section.

Answer to Problem 19.1P

The section modulus is $\underset{¯}{30.8\times {10}^{-5}{\text{m}}^{\text{3}}/\text{m}\text{of the wall}}$.

Explanation of Solution

Given information:

The allowable pressure ${\sigma }_{\text{all}}$ is $170{\text{MN/m}}^{\text{2}}$.

Calculation:

For top block,

Consider the maximum moment occurs at distance $z_1$ above $B_1$ (zero shear force).

$\begin{array}{l}{B}_1={\sigma }_a{z}_1\\ 72.02=49.5\times z_1\\ z_1=1.455\text{m}\end{array}$

Find the maximum moment as follows:

$\begin{array}{c}{M}_{\max }=B_1{z}_1-{\sigma }_a{z}_1\left(\frac{z_1}{2}\right)\\ =\left(72.02\times 1.455\right)-49.5\times 1.455\times \left(\frac{1.455}{2}\right)\\ =52.39\text{kN}\cdot \text{m/m}\end{array}$

The maximum moment occurs at C in the lower block

Find the maximum moment at lower block as follows:

$\begin{array}{c}{M}_{\max }={\sigma }_a\left(1\right)\left(0.5\right)\\ =49.5\times \left(1\right)\left(0.5\right)\\ =24.75\text{kN}\cdot \text{m/m}\end{array}$

Consider that the higher value of maximum moment is $52.39\text{kN}\cdot \text{m/m}$

Find the required section modulus using the formula:

$\begin{array}{c}S=\frac{M_{\max }}{{\sigma }_{\text{all}}}\\ =\frac{52.39}{170{\text{MN/m}}^{\text{2}}}\\ =\frac{52.39}{170\times {10}^3{\text{kN/m}}^{\text{2}}}\\ =30.8\times {10}^{-5}{\text{m}}^{\text{3}}/\text{m}\text{of the wall}\end{array}$

Refer Table 18.1, “Properties of some commercially available sheet-pile section” in the textbook.

Take the section designation as PZ-22 according to the values.

Therefore, the section modulus is $\underset{¯}{30.8\times {10}^{-5}{\text{m}}^{\text{3}}/\text{m}\text{of the wall}}$.

To determine

Find the maximum moment for the two wales.

Answer to Problem 19.1P

The maximum moment for the wall at B is $\underset{¯}{341.06\text{kN}\cdot \text{m}}$.

The maximum moment for the wall at C is $\underset{¯}{348.06\text{kN}\cdot \text{m}}$.

Explanation of Solution

Find the maximum moment for the wall at B,

$\begin{array}{c}{M}_{\max }=\frac{\left(B_1+B_2\right)s^2}{8}\\ =\frac{\left(72.02+37.12\right)\times 5^2}{8}\\ =341.06\text{kN}\cdot \text{m}\end{array}$

Find the maximum moment for the wall at C,

$\begin{array}{c}{M}_{\max }=\frac{C{s}^2}{8}\\ =\frac{111.38\times 5^2}{8}\\ =348.06\text{kNm}\end{array}$

The maximum moment for the wall at B is $\underset{¯}{341.06\text{kN}\cdot \text{m}}$.

The maximum moment for the wall at C is $\underset{¯}{348.06\text{kN}\cdot \text{m}}$.