
The precession axis, rates of precession, and the spin rate of the satellite after the impact.
Answer to Problem 18.129P
The precession along x, y, and z axis
The precession rate
The spin rate
Explanation of Solution
Given information:
The weight of geostationary satellite (W) is 800 lb.
The angular velocity of the satellite
The weight of a meteorite
The travelling velocity of the meteorite
The distance value b is 20 in..
The radii of gyration of the satellite along x, y, and z direction (
Calculation:
Determine the mass of the satellite (m).
Here, g is the acceleration due to gravity.
Substitute 800 lb for W and
Determine the principal moment of inertia along x axis.
Substitute
Determine the principal moment of inertia along y axis.
Substitute
Determine the principal moment of inertia along z axis.
Substitute
Determine the mass of the meteorite
Substitute 6 oz for
Determine the initial moment of meteorite
Substitute
Consider that the position of the satellite mass center plus the meteorite is essentially that of the satellite alone.
Determine the position of the point B relative to the mass center.
Here, x is the horizontal distance and y is the vertical distance.
Substitute 42 in. for x and 20 in. for y.
The angular velocity of satellite before impact
The angular velocity of satellite before impact along x, y, and z axis is
Determine the angular momentum of satellite–meteorite system before impact
Substitute
Principle of impulse and momentum for satellite–meteorite system:
The value of moments about G is
The expression for
Determine the angular velocity about x axis.
Substitute
Determine the angular velocity about y axis.
Substitute
Determine the angular velocity about z axis.
Substitute
Determine the vector format of angular velocity using the relation;
Substitute
Determine the magnitude of the angular velocity
Substitute
Determine the magnitude of angular momentum
Substitute
Motion after impact:
The moment of inertia about x and y axis is equal, the body moves as an axisymmetrical body with the y axis as the symmetry axis.
The moment of inertia about the symmetry axis is
The moment of inertia about a transverse axis through G is
The precession is retrograde when the value of
Determine the angle
Substitute
Determine the angle
Substitute
Determine the angle
Substitute
Thus, the precession along x, y, and z axis
The angle
Determine the angle
Substitute
Determine the value of
Substitute
Draw the free body diagram of precession and spin axis as in Figure (1).
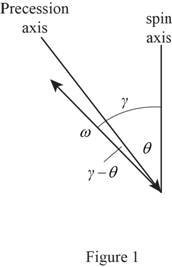
Draw the free body diagram of triangle of vector addition as in Figure (2).

Write the relation between the angles using the sine law.
Determine the precession rate
Substitute
Therefore, the precession rate
Determine the rate of spin
Substitute
The precession is retrograde due to value of
Therefore, the spin rate
Want to see more full solutions like this?
Chapter 18 Solutions
VECTOR MECHANIC
- (◉ Home - my.uah.edu Homework#5 MasteringEngineering Mastering X + 8 https://session.engineering-mastering.pearson.com/myct/itemView?assignmentProblemID=18992148&offset=nextarrow_forward(◉ Home - my.uah.edu Homework#5 MasteringEngineering Mastering X + 8 https://session.engineering-mastering.pearson.com/myct/itemView?assignmentProblemID=18992144&offset=nextarrow_forwardCalculate the forces in members BC, BG & FG of the truss shown using the Method of Sections. For your answer, provide atruss diagram of the calculated member forces and indicate whether the member is in Tension (+) or Compression (-)arrow_forwardThe enthalpy of fusion for water is 6.01 kJ/mol. Calculate the entropy change for 1.0 mole of ice melting to form liquid at 273 Karrow_forwardCalculate the entropy change for 1.00 mol of an ideal gas expanding isothermally from a volume of 24.4 L to 48.8 L.arrow_forwardDetermine the endurance limit.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY