
Concept explainers
Estimate the air temperatures and corresponding speeds of sound at altitudes of
Answer to Problem 35P
The air temperatures and corresponding speeds of sound at altitudes of
Explanation of Solution
Given data:
Refer to Table given in problem 18.35 in textbook,
The air temperature at altitude
The air temperature at altitude
The speed of sound at altitude
The speed of sound at altitude
The air temperature at altitude
The air temperature at altitude
The speed of sound at altitude
The speed of sound at altitude
Formula used:
Formula for the linear interpolation is,
Calculation:
To find the air temperature at altitude
The diagrammatic representation for the given value is drawn below,
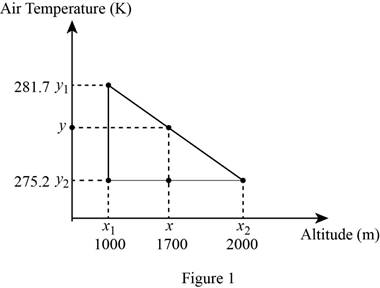
Substitute
Equation (2) can be reduced as follows,
Reduce the equation as follows,
Therefore, the air temperature at an altitude
To find the speed of sound at an altitude
The diagrammatic representation for the given value is drawn below,
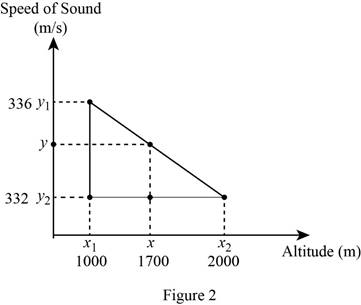
Substitute
Equation (3) can be reduced as follows,
Reduce the equation as,
Therefore, the approximate value of speed of sound at an altitude
To find the air temperature at altitude
The diagrammatic representation for the given value is drawn below,
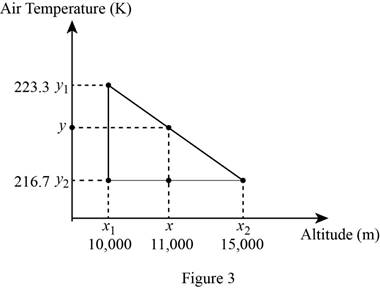
Substitute
Equation (4) can be reduced as follows
Reduce the equation as follows,
Therefore, the air temperature at an altitude
To find the speed of sound at an altitude
The diagrammatic representation for the given value is drawn below,
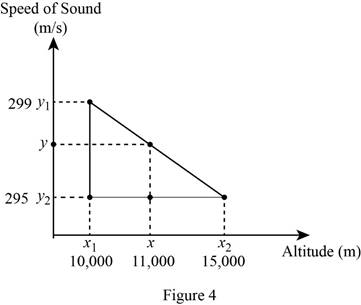
Substitute
Equation (5) can be reduced as follows
Reduce the equation as follows,
Therefore, the approximate value of speed of sound at an altitude
Conclusion:
Thus, the air temperatures and corresponding speeds of sound at altitudes of
Want to see more full solutions like this?
Chapter 18 Solutions
EP WEBASSIGN FOR MOAVENI'S ENGINEERING
- What are the total earned work hours at completion for the column forms?arrow_forward6000 units have been installed to date with 9,000 units to install. Labor costs are $23,300.00 to date. What is the unit cost for labor to date?arrow_forwardThe base rate for labor is $15/hr. The labor burden is 35% and 3% for small tools for the labor. There are 1000 units to install. Records indicate that trade workers can install 10 units per hour, per trade worker. The owners need 15% overhead and profit to pay bills, pay interest on loan and provide some profit to the partners. What is the minimum bid assuming no risk avoidance factor?arrow_forward
- 5. (20 Points) Consider a channel width change in the same 7-foot wide rectangular in Problem 4. The horizontal channel narrows as depicted below. The flow rate is 90 cfs, and the energy loss (headloss) through the transition is 0.05 feet. The water depth at the entrance to the transition is initially 4'. 1 b₁ TOTAL ENERGY LINE V² 129 У1 I b₂ TOP VIEW 2 PROFILE VIEW h₁ = 0.05 EGL Y₂ = ? a) b) c) 2 Determine the width, b₂ that will cause a choke at location 2. Determine the water depth at the downstream end of the channel transition (y₂) section if b₂ = 5 feet. Calculate the change in water level after the transition. Plot the specific energy diagram showing all key points. Provide printout in homework. d) What will occur if b₂ = = 1.5 ft.?arrow_forward4. (20 Points) A transition section has been proposed to raise the bed level a height Dz in a 7-foot wide rectangular channel. The design flow rate in the channel is 90 cfs, and the energy loss (headloss) through the transition is 0.05 feet. The water depth at the entrance to the transition section is initially 4 feet. b₁ = b = b2 1 TOTAL ENERGY LINE V² 129 Ут TOP VIEW 2 hloss = 0.05 " EGL Y₂ = ? PROFILE VIEW a) Determine the minimum bed level rise, Dz, which will choke the flow. b) If the step height, Dz = 1 ft, determine the water depth (y2) at the downstream end of the channel transition section. Calculate the amount the water level drops or rises over the step. c) Plot the specific energy diagram showing all key points. Provide printout in Bework. d) What will occur if Dz = 3.0 ft.?. Crest Front Viewarrow_forward1. (20 Points) Determine the critical depth in the trapezoidal drainage ditch shown below. The slope of the ditch is 0.0016, the side slopes are 1V:2.5H, the bottom width is b = 14', and the design discharge is 500 cfs. At this discharge the depth is y = 4.25'. Also, determine the flow regime and calculate the Froude number. Ye= ? Z barrow_forward
 Engineering Fundamentals: An Introduction to Engi...Civil EngineeringISBN:9781305084766Author:Saeed MoaveniPublisher:Cengage Learning
Engineering Fundamentals: An Introduction to Engi...Civil EngineeringISBN:9781305084766Author:Saeed MoaveniPublisher:Cengage Learning
