Chapter 18, Problem 31CE

To determine

Determine a seasonal index for each of the four quarters.

Find the number of visitors for each quarter of 2017 if 10% increase in the total number of visitors in 2016.

Determine the trend equation.

Project the number of visitors for 2017.

Find the seasonally adjusted forecasts.

Identify the best forecast.

Answer to Problem 31CE

The seasonal indexes for the four quarters are 1.2046, 1.0206, 0.6297 and 01.1451, respectively.

The number of visitors for each quarter of 2017 if 10% increase in the total number of visitors in 2016 is 255.25 visitors per quarter.

The trend equation is $\widehat{Y}=50.127+6.617t$.

The number of visitors for 2017 are 242.0171, 248.634, 255.2509 and 261.8678.

The seasonally adjusted forecasts are 291.5338, 253.7559, 160.7315 and 299.8648.

The best forecast is the fourth quarter of 2017.

Explanation of Solution

Calculation:

Four-Year moving average:

$\text{Four-year moving average}=\frac{\text{sum of the four concequent Visitors}}{4}$.

Centered Moving Average:

$\text{Centered moving average}=\frac{\text{sum of the two concequent moving averages}}{2}$.

Specific seasonal index:

$\text{Specific seasonal index}=\frac{\text{Visitors}}{\text{Centered moving average}}$

Year	Quarter	Visitors	Four-quarter moving average	Centered Moving average	Specific seasonal
2010	1	86
	2	62
	3	28		70	0.4
	4	94	67.5	75	1.253333
2011	1	106	72.5	80	1.325
	2	82	77.5	85	0.964706
	3	48	82.5	91.75	0.523161
	4	114	87.5	100.75	1.131514
2012	1	140	96	109.75	1.275626
	2	120	105.5	119	1.008403
	3	82	114	126.75	0.646943
	4	154	124	132	1.166667
2013	1	162	129.5	136.75	1.184644
	2	140	134.5	141.5	0.989399
	3	100	139	147.25	0.679117
	4	174	144	154.5	1.126214
2014	1	188	150.5	162	1.160494
	2	172	158.5	168.5	1.020772
	3	128	165.5	174	0.735632
	4	198	171.5	180.25	1.098474
2015	1	208	176.5	187.25	1.110814
	2	202	184	193.25	1.045278
	3	154	190.5	200.75	0.767123
	4	220	196	210.25	1.046373
2016	1	246	205.5	219.5	1.120729
	2	240	215	228	1.052632
	3	190	224
	4	252	232

The Quarterly indexes are,

	I	II	III	IV
2010			0.4	1.253333
2011	1.325	0.964706	0.523161	1.131514
2012	1.275626	1.008403	0.646943	1.166667
2013	1.184644	0.989399	0.679117	1.126214
2014	1.160494	1.020772	0.735632	1.098474
2015	1.110814	1.045278	0.767123	1.046373
2016	1.120729	1.052632
Mean	1.1962	1.0135	0.6253	1.1371

Seasonal index:

$\text{Seasonal Index}=\text{Mean of the quarter}\times \text{Correction Factor}$

Here, $\text{Correction Factor}=\frac{4}{\text{Sum of the means of the quarters}}$.

Therefore,

$\begin{array}{c}\text{Correction Factor}=\frac{4}{\text{1}\text{.1962+1}\text{.0135+0}\text{.6253+1}\text{.1371}}\\ =\frac{4}{3.9721}\\ =1.00703\end{array}$

The seasonal indexes are,

	I	II	III	IV
2010			0.4	1.253333
2011	1.325	0.964706	0.523161	1.131514
2012	1.275626	1.008403	0.646943	1.166667
2013	1.184644	0.989399	0.679117	1.126214
2014	1.160494	1.020772	0.735632	1.098474
2015	1.110814	1.045278	0.767123	1.046373
2016	1.120729	1.052632
Mean	1.1962	1.0135	0.6253	1.1371
Seasonal Index	$\begin{array}{l}1.1962\times 1.00703\\ =1.2046\end{array}$	$\begin{array}{l}1.0135\times 1.00703\\ =1.0206\end{array}$	$\begin{array}{l}0.6253\times 1.00703\\ =0.6297\end{array}$	$\begin{array}{l}1.1371\times 1.00703\\ =1.1451\end{array}$

The total number of visitors in year 2016 is $928\left(=246+240+190+252\right)$.

The 10% of 928 visitors is $\approx 93\left(928\times 0.10=92.8\right)$.

The number of visitors in 2017 is $1,021\left(=928+93\right)$.

Therefore, the number of visitors in each quarter of 2017 is $\frac{1,021}{4}=255.25$.

Trend Equation:

Step-by-step procedure to obtain the regression using the Excel:

• Enter the data for Year, Visitors and t in Excel sheet.
• Go to Data Menu.
• Click on Data Analysis.
• Select ‘Regression’ and click on ‘OK’
• Select the column of Visitors under ‘Input Y Range’.
• Select the column of t under ‘Input X Range’.
• Click on ‘OK’.

Output for the Regression obtained using the Excel is as follows:

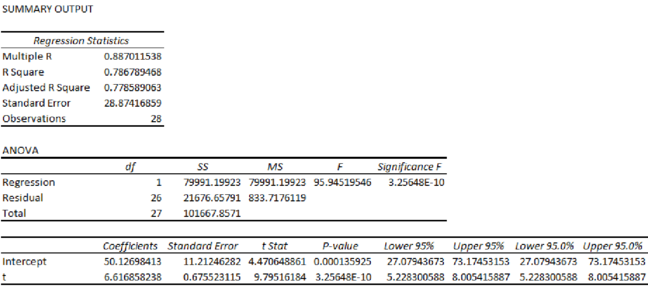
From the output, the regression equation is $\widehat{Y}=50.127+6.617t$.

Projection of the number of visitors for 2017:

The t value for first quarter of 2017 is 29.

$\begin{array}{c}\widehat{Y}=50.127+\left(6.617\times 29\right)\\ =242.0171\end{array}$

The t value for second quarter of 2017 is 30.

$\begin{array}{c}\widehat{Y}=50.127+\left(6.617\times 30\right)\\ =248.634\end{array}$

The t value for third quarter of 2017 is 31.

$\begin{array}{c}\widehat{Y}=50.127+\left(6.617\times 31\right)\\ =255.2509\end{array}$

The t value for third quarter of 2017 is 32.

$\begin{array}{c}\widehat{Y}=50.127+\left(6.617\times 32\right)\\ =261.8678\end{array}$

Seasonally Adjusted Forecast:

Estimated Visitors	Seasonal Index	$\text{Forecast}=\text{Estimated Visitors}\times \text{Seasonal Index}$
242.0171	1.2046	291.5338
248.634	1.0206	253.7559
255.2509	0.6297	160.7315
261.8678	1.1451	299.8648

The seasonal index for the fourth quarter is high compared with remaining three quarters. Hence, the forecast for the fourth quarter is best.