Chapter 18, Problem 26CE

a.

To determine

Determine the typical seasonal patterns for the production data using the ratio-to-moving-average method.

Answer to Problem 26CE

The typical seasonal patterns for sales are 0.7549, 0.9913, 1.4043 and 0.8495, respectively.

Explanation of Solution

Calculation:

Four-Year moving average:

$\text{Four-year moving average}=\frac{\text{sum of the four consequent production}}{4}$

Centered Moving Average:

$\text{Centered moving average}=\frac{\text{sum of the two consequent moving averages}}{2}$

Specific seasonal index:

$\text{Specific seasonal index}=\frac{\text{production}}{\text{Centered moving average}}$

Year	Quarter	Board ft Millions	Four-quarter moving average	Centered Moving average	Specific seasonal
2012	Winter	7.8
	Spring	10.2
	Summer	14.7		10.3875	1.41516
	Fall	9.3	10.5	10.45	0.88995
2013	Winter	6.9	10.275	10.975	0.6287
	Spring	11.6	10.625	11.325	1.02428
	Summer	17.5	11.325	11.575	1.51188
	Fall	9.3	11.325	11.5875	0.80259
2014	Winter	8.9	11.825	11.075	0.80361
	Spring	9.7	11.35	10.9	0.88991
	Summer	15.3	10.8	11.225	1.36303
	Fall	10.1	11	11.7875	0.85684
2015	Winter	10.7	11.45	12.3125	0.86904
	Spring	12.4	12.125	12.575	0.98608
	Summer	16.8	12.5	12.4625	1.34804
	Fall	10.7	12.65	12.425	0.86117
2016	Winter	9.2	12.275	12.6125	0.72944
	Spring	13.6	12.575	12.6	1.07937
	Summer	17.1	12.65
	Fall	10.3	12.55

The Quarterly indexes are,

	Winter	Spring	Summer	Fall
2012			1.415162	0.889952
2013	0.628702	1.024283	1.511879	0.802589
2014	0.803612	0.889908	1.363029	0.85684
2015	0.869036	0.986083	1.348044	0.861167
2016	0.729435	1.079365
Mean	0.757696	0.99491	1.409529	0.852637

Typical Seasonal index:

$\text{Seasonal Index}=\text{Mean of the quarter}\times \text{Correction Factor}$

Here, $\text{Correction Factor}=\frac{4}{\text{Sum of the means of the quarters}}$.

Therefore,

$\begin{array}{c}\text{Correction Factor}=\frac{4}{4.014771}\\ =0.996321\end{array}$

The typical seasonal indexes are,

	Winter	Spring	Summer	Fall
2012			1.415162	0.889952
2013	0.628702	1.024283	1.511879	0.802589
2014	0.803612	0.889908	1.363029	0.85684
2015	0.869036	0.986083	1.348044	0.861167
2016	0.729435	1.079365
Mean	0.757696	0.99491	1.409529	0.852637
Typical Index	0.7549	0.9913	1.4043	0.8495

b.

To determine

Interpret the typical seasonal pattern.

Explanation of Solution

The typical seasonal index for the Summer quarter is 1.4043, which is largest compared with other three quarters. That is, the production is largest in the third quarter and moreover, it represent above the average quarters because seasonal index is greater than 1. The Winter, Spring and Fall quarters represent below the average quarters because seasonal indexes for the three quarters are less than 1.

c.

To determine

Determine the trend equation.

Answer to Problem 26CE

The trend equation is $\widehat{Y}=10.11077+0.142298t$.

Explanation of Solution

Calculation:

Deseasonalization:

$\text{Deseasonalization}=\frac{\text{Original production}}{\text{Typical Index values}}$

Board ft Millions	Typical Seasonal Index	Deseasonalized production
7.8	0.7549	10.33249437
10.2	0.9913	10.28951881
14.7	1.4043	10.46784875
9.3	0.8495	10.94761624
6.9	0.7549	9.140283481
11.6	0.9913	11.70180571
17.5	1.4043	12.4617247
9.3	0.8495	10.94761624
8.9	0.7549	11.78964101
9.7	0.9913	9.785130637
15.3	1.4043	10.89510788
10.1	0.8495	11.88934667
10.7	0.7549	14.17406279
12.4	0.9913	12.50882679
16.8	1.4043	11.96325571
10.7	0.8495	12.5956445
9.2	0.7549	12.18704464
13.6	0.9913	13.71935842
17.1	1.4043	12.17688528
10.3	0.8495	12.12477928

Assign t value as 1 for first quarter of 2012, 2 for the second quarter of 2012 and so on.

Step-by-step procedure to obtain the regression using the Excel:

• Enter the data for Deseasonalized production and t in Excel sheet.
• Go to Data Menu.
• Click on Data Analysis.
• Select ‘Regression’ and click on ‘OK’
• Select the column of Deseasonalized production under ‘Input Y Range’.
• Select the column of t under ‘Input X Range’.
• Click on ‘OK’.

Output for the Regression obtained using the Excel is as follows:

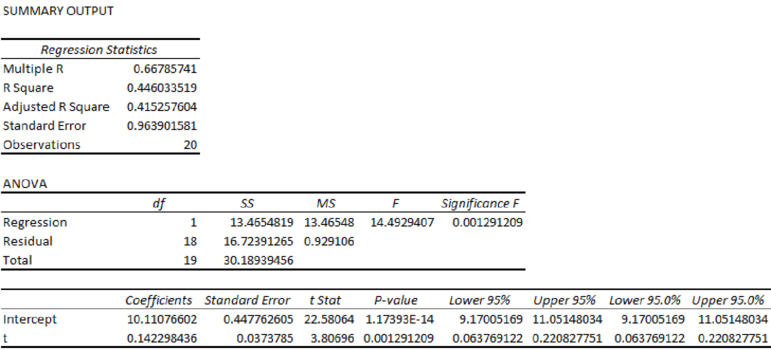
From the Excel output, the regression equation is $\widehat{Y}=10.11077+0.142298t$.

d.

To determine

Find the seasonally adjusted production for four quarters of 2017.

Answer to Problem 26CE

The seasonally adjusted production for four quarters of 2017 are 9.8884, 13.1261, 18.7946 and 11.4903, respectively.

Explanation of Solution

Calculation:

From the output, the regression equation is $\widehat{Y}=10.11077+0.142298t$.

The t value for first quarter of 2017 is 21.

$\begin{array}{c}\widehat{Y}=10.11077+0.142298t\\ =10.11077+\left(0.142298\times 21\right)\\ =13.0990\end{array}$

The t value for second quarter of 2017 is 22.

$\begin{array}{c}\widehat{Y}=10.11077+0.142298t\\ =10.11077+\left(0.142298\times 22\right)\\ =13.2413\end{array}$

The t value for third quarter of 2017 is 23.

$\begin{array}{c}\widehat{Y}=10.11077+0.142298t\\ =10.11077+\left(0.142298\times 23\right)\\ =13.3836\end{array}$

The t value for fourth quarter of 2017 is 24.

$\begin{array}{c}\widehat{Y}=10.11077+0.142298t\\ =10.11077+\left(0.142298\times 24\right)\\ =13.5259\end{array}$

Seasonally Adjusted Forecast:

Estimated Visitors	Seasonal Index	$\text{Forecast}=\text{Estimated Visitors}\times \text{Seasonal Index}$
13.0990	0.7549	9.8884
13.2413	0.9913	13.1261
13.3836	1.4043	18.7946
13.5259	0.8495	11.4903