
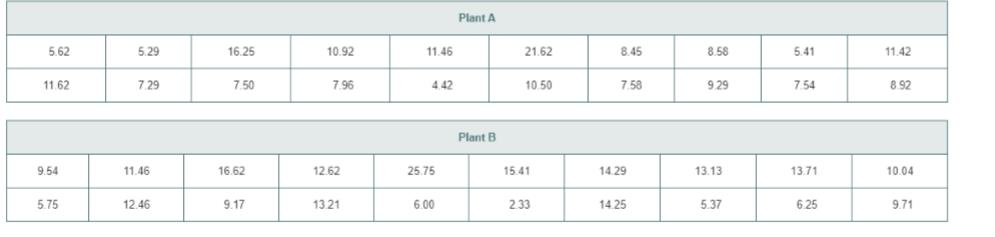
In many manufacturing processes, the term work-in-process (often abbreviated WIP) is used. At the LSS Publishing book manufacturing plants, WIP represents the time it takes for sheets from a press to be folded, gathered, sewn, tipped on end sheets, and bound together to form a book, and the book placed in a packing carton. The operational definition of the variable of interest, processing time, is the number of days (measured in hundredths) from when the sheets come off the press to when the book is placed in a packing cartoon. The company has the business objective of determining whether there are differences in the WIP between plants. Data have been collected from samples of 20 books at each production plants. The data, stored in WIP, are as follows:
Completely analyse the data.
Completely analyze the data to determine whether there are differences in the WIP between both plants.
Explanation of Solution
The data is provided for work-in-process (WIP) for Plant A and Plant B. The data has been collected from samples of 20 books at each of the two production plants.
The descriptive statistics of the data can be calculated using the Minitab as follows:
Software procedure:
Step by step procedure to find the descriptive statistics by Minitab software is as follows:
Enter the data for Plant A and Plant B in the worksheet.
Go to Stat < Basic Statistics < Display Descriptive Statistics.
Click on Variables section.
Double-click C1 Plant A and C2 Plant B to add in the Variables box.
Click on the Statistics option and check the required statistics option.
Click Ok.
The output of Minitab software is:
It can be assumed that the data of the two plants A and B are from independent groups rather being from matched or paired group.
Either the pooled-variance t-test or the separate variance t-test for the difference in two means if the distribution of the time is normal in both plants. If the distribution is not normal, the results of t test can be compared to Wilcoxon rank sum test.
The assumption of Normality can be checked with the help of Minitab software.
The normal probability plot for Plant A is:
Software procedure:
Step by step procedure to find the descriptive statistics by Minitab software is as follows:
Go to Graph < Probability Plot < Single.
Click Ok.
Click on Variables section.
Double-click C1 Plant A to add in the Graph Variables box.
Click Ok.
The output of Minitab software is:
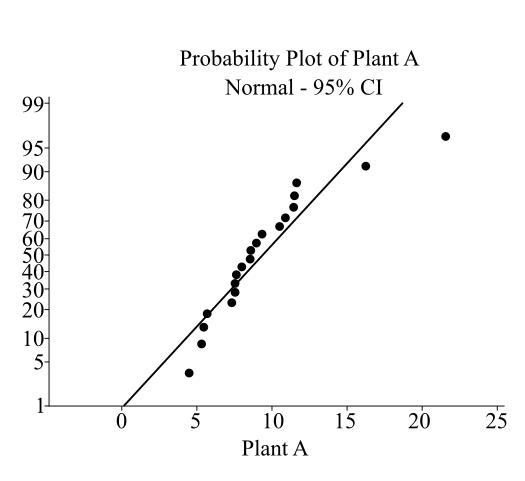
The normal probability plot for Plant B is
Software procedure:
Step by step procedure to find the descriptive statistics by Minitab software is as follows:
Go to Graph < Probability Plot < Single.
Click Ok.
Click on Variables section.
Double-click C1 Plant A to add in the Graph Variables box.
Click Ok.
The output of Minitab software is:
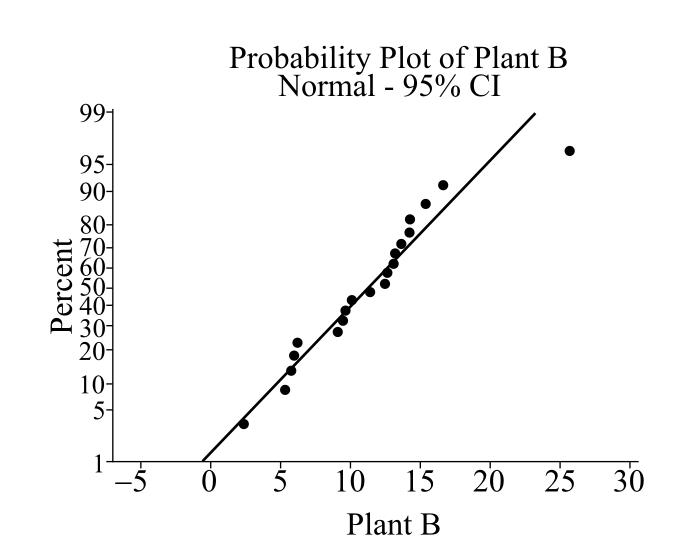
From the obtained normal probability plots, the processing time appears to be right-skewed as they largely deviate from the straight line.
Both the t tests, whether it is pooled variance or similar variance, give relevant result when the parent population follows normal distribution. Nevertheless, a Wilcoxon rank sum test might be more appropriate.
Further, equality of variance should be checked.
Test whether there is difference in variance of processing time of plant A and plant B or not.
Answer to Problem 1CRP
There is insufficient evidence to conclude that the variances of processing time of plant A and plant B differ significantly.
Explanation of Solution
The following steps are followed to test whether variances are equal or not.
Step 1:
The null and the alternative hypotheses are:
Here,
Step 2:
The size of both the samples is 20. The level of significance
Step 3:
The
Step 4:
Use Minitab to find test statistic and
Software procedure:
Step by step procedure to perform 2 variances test is given below:
Choose Stat > Basic Statistics > 2 Variances.
From the drop down, select Each sample is in its own column.
Click on Variables section.
Double-click C1 Plant A to add in the Sample 1 box and double-click C2 Plant B to add in the Sample 2 box.
Click Options and check Use test and confidence interval based in normal distribution.
Click Ok.
The Minitab output shows that the test statistic is 1.64 and
Step 5:
Decision based on the
If
If
Since
At
Test whether the mean processing time of plant A and plant B is different.
Answer to Problem 1CRP
There is insufficient evidence to conclude that there is a significant difference in the mean processing time of plant A and plant B.
Explanation of Solution
The following steps are followed to test whether population means are equal or not.
Step 1:
The null and the alternative hypotheses are:
Here,
Step 2:
The size of both the samples is 20. The level of significance
Step 3:
From the above part, it was concluded that the variance processing time of plant A and plant B are significantly not different. Thus, pooled variance
Step 4:
Use Minitab to find test statistic and
Software procedure:
Step by step procedure to perform 2 sample t test is given below:
Choose Stat > Basic Statistics > 2-Sample t.
From the drop down, select Each sample is in its own column.
Click on Variables section.
Double-click C1 Plant A to add in the Sample 1 box and double-click C2 Plant B to add in the Sample 2 box.
Click Options.
Tick the option Assume equal variances.
Click Ok.
Click Ok.
The Minitab output shows that the test statistics is
Step 5:
Decision based on the
If
If
Since
There is insufficient evidence to conclude that the population means are significantly different.
Test whether the median processing time of plant A and plant B is different.
Answer to Problem 1CRP
There is insufficient evidence to conclude that there is significant difference in the median processing time of plant A and plant B.
Explanation of Solution
The following steps are followed to test the median of the two populations.
Step 1:
The null and the alternative hypotheses are:
Here,
Step 2:
The size of both the samples is 20. The level of significance
Step 3:
From the above parts, it was concluded that the mean processing time of plant A and plant B are significantly not different as well as the population deviate from the normal distribution. Thus, Mann Whitney test (Wilcoxon rank sum test) is used to compare the medians and to validate the results.
Step 4:
Use Minitab to find test statistic and
Software procedure:
Step by step procedure to perform 2 sample t test is given below:
Choose Stat > Nonparametrics > Mann-Whitney.
Click on Variables section.
Double-click C1 Plant A to add in the First Sample box and double-click C2 Plant B to add in the Second Sample box.
Click Ok.
The Minitab output shows that test statistics is 345.5 and
Step 5:
Decision based on the
If
If
Since
There is insufficient evidence to conclude that the population medians are significantly different.
Therefore, from the above results, it can be concluded that both t test and Wilcoxon rank sum test give the same result that is processing time of Plant A and Plant B does not differ significantly.
Want to see more full solutions like this?
Chapter 18 Solutions
Basic Business Statistics, Student Value Edition
- « CENGAGE MINDTAP Quiz: Chapter 38 Assignment: Quiz: Chapter 38 ips Questions ra1kw08h_ch38.15m 13. 14. 15. O Which sentence has modifiers in the correct place? O a. When called, she for a medical emergency responds quickly. b. Without giving away too much of the plot, Helena described the heroine's actions in the film. O c. Nearly the snakebite victim died before the proper antitoxin was injected. . O O 16 16. O 17. 18. O 19. O 20 20. 21 21. 22. 22 DS 23. 23 24. 25. O O Oarrow_forwardQuestions ra1kw08h_ch36.14m 12. 13. 14. 15. 16. Ӧ 17. 18. 19. OS 20. Two separate sentences need Oa. two separate subjects. Ob. two dependent clauses. c. one shared subject.arrow_forwardCustomers experiencing technical difficulty with their Internet cable service may call an 800 number for technical support. It takes the technician between 30 seconds and 11 minutes to resolve the problem. The distribution of this support time follows the uniform distribution. Required: a. What are the values for a and b in minutes? Note: Do not round your intermediate calculations. Round your answers to 1 decimal place. b-1. What is the mean time to resolve the problem? b-2. What is the standard deviation of the time? c. What percent of the problems take more than 5 minutes to resolve? d. Suppose we wish to find the middle 50% of the problem-solving times. What are the end points of these two times?arrow_forward
- Exercise 6-6 (Algo) (LO6-3) The director of admissions at Kinzua University in Nova Scotia estimated the distribution of student admissions for the fall semester on the basis of past experience. Admissions Probability 1,100 0.5 1,400 0.4 1,300 0.1 Click here for the Excel Data File Required: What is the expected number of admissions for the fall semester? Compute the variance and the standard deviation of the number of admissions. Note: Round your standard deviation to 2 decimal places.arrow_forward1. Find the mean of the x-values (x-bar) and the mean of the y-values (y-bar) and write/label each here: 2. Label the second row in the table using proper notation; then, complete the table. In the fifth and sixth columns, show the 'products' of what you're multiplying, as well as the answers. X y x minus x-bar y minus y-bar (x minus x-bar)(y minus y-bar) (x minus x-bar)^2 xy 16 20 34 4-2 5 2 3. Write the sums that represents Sxx and Sxy in the table, at the bottom of their respective columns. 4. Find the slope of the Regression line: bi = (simplify your answer) 5. Find the y-intercept of the Regression line, and then write the equation of the Regression line. Show your work. Then, BOX your final answer. Express your line as "y-hat equals...arrow_forwardApply STATA commands & submit the output for each question only when indicated below i. Generate the log of birthweight and family income of children. Name these new variables Ibwght & Ifaminc. Include the output of this code. ii. Apply the command sum with the detail option to the variable faminc. Note: you should find the 25th percentile value, the 50th percentile and the 75th percentile value of faminc from the output - you will need it to answer the next question Include the output of this code. iii. iv. Use the output from part ii of this question to Generate a variable called "high_faminc" that takes a value 1 if faminc is less than or equal to the 25th percentile, it takes the value 2 if faminc is greater than 25th percentile but less than or equal to the 50th percentile, it takes the value 3 if faminc is greater than 50th percentile but less than or equal to the 75th percentile, it takes the value 4 if faminc is greater than the 75th percentile. Include the outcome of this code…arrow_forward
- solve this on paperarrow_forwardApply STATA commands & submit the output for each question only when indicated below i. Apply the command egen to create a variable called "wyd" which is the rowtotal function on variables bwght & faminc. ii. Apply the list command for the first 10 observations to show that the code in part i worked. Include the outcome of this code iii. Apply the egen command to create a new variable called "bwghtsum" using the sum function on variable bwght by the variable high_faminc (Note: need to apply the bysort' statement) iv. Apply the "by high_faminc" statement to find the V. descriptive statistics of bwght and bwghtsum Include the output of this code. Why is there a difference between the standard deviations of bwght and bwghtsum from part iv of this question?arrow_forwardAccording to a health information website, the distribution of adults’ diastolic blood pressure (in millimeters of mercury, mmHg) can be modeled by a normal distribution with mean 70 mmHg and standard deviation 20 mmHg. b. Above what diastolic pressure would classify someone in the highest 1% of blood pressures? Show all calculations used.arrow_forward
- Write STATA codes which will generate the outcomes in the questions & submit the output for each question only when indicated below i. ii. iii. iv. V. Write a code which will allow STATA to go to your favorite folder to access your files. Load the birthweight1.dta dataset from your favorite folder and save it under a different filename to protect data integrity. Call the new dataset babywt.dta (make sure to use the replace option). Verify that it contains 2,998 observations and 8 variables. Include the output of this code. Are there missing observations for variable(s) for the variables called bwght, faminc, cigs? How would you know? (You may use more than one code to show your answer(s)) Include the output of your code (s). Write the definitions of these variables: bwght, faminc, male, white, motheduc,cigs; which of these variables are categorical? [Hint: use the labels of the variables & the browse command] Who is this dataset about? Who can use this dataset to answer what kind of…arrow_forwardApply STATA commands & submit the output for each question only when indicated below İ. ii. iii. iv. V. Apply the command summarize on variables bwght and faminc. What is the average birthweight of babies and family income of the respondents? Include the output of this code. Apply the tab command on the variable called male. How many of the babies and what share of babies are male? Include the output of this code. Find the summary statistics (i.e. use the sum command) of the variables bwght and faminc if the babies are white. Include the output of this code. Find the summary statistics (i.e. use the sum command) of the variables bwght and faminc if the babies are male but not white. Include the output of this code. Using your answers to previous subparts of this question: What is the difference between the average birthweight of a baby who is male and a baby who is male but not white? What can you say anything about the difference in family income of the babies that are male and male…arrow_forwardA public health researcher is studying the impacts of nudge marketing techniques on shoppers vegetablesarrow_forward

 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning


