
Concept explainers
As in Figure P18.16, a simple harmonic oscillator is attached to a rope of linear mass density 5.4 × 10−2 kg/m, creating a standing transverse wave. There is a 3.6-kg block hanging from the other end of the rope over a pulley. The oscillator has an angular frequency of 43.2 rad/s and an amplitude of 24.6 cm. a. What is the distance between adjacent nodes? b. If the angular frequency of the oscillator doubles, what happens to the distance between adjacent nodes? c. If the mass of the block is doubled instead, what happens to the distance between adjacent nodes? d. If the amplitude of the oscillator is doubled, what happens to the distance between adjacent nodes?
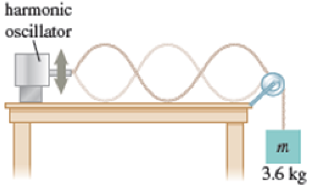
FIGURE P18.16
(a)
The distance between the adjacent nodes.
Answer to Problem 16PQ
The distance between the adjacent nodes is
Explanation of Solution
Given that the linear mass density of the rope is
Write the expression for the wavelength of the wave.
Here,
Write the expression for the speed of the wave.
Here,
Write the equation to find the frequency of the wave.
Here,
Use equation (III) and (II) in (I).
Write the expression for the tension force on the rope (it is equal to the weight of the block hanged).
Here,
Use above expression in equation (IV).
The distance between the adjacent nodes is equal to half the wavelength of the wave.
Rewrite above equation using equation (V).
Conclusion:
Substitute
Therefore, the distance between the adjacent nodes is
(b)
The distance between the adjacent nodes when the angular frequency is doubled.
Answer to Problem 16PQ
The distance between the adjacent nodes when the angular frequency is doubled is
Explanation of Solution
Equation (VI) gives the expression for the distance between the nodes.
From the above equation it is clear that wavelength is inversely proportional to angular frequency.
The angular frequency is doubled. Replace
Conclusion:
Substitute
Therefore, distance between the adjacent nodes when the angular frequency is doubled is
(c)
The distance between the adjacent nodes if the mass of the block is doubled.
Answer to Problem 16PQ
The distance between the adjacent nodes if the mass of the block is doubled is
Explanation of Solution
Equation (VI) gives the expression for the distance between the nodes.
When the mass of the block is doubled,
Conclusion:
Substitute
Therefore, the distance between the adjacent nodes if the mass of the block is doubled is
(d)
The distance between the nodes if the amplitude of the oscillator is doubled.
Answer to Problem 16PQ
The distance between the nodes remains the same even if the amplitude of the oscillator is doubled.
Explanation of Solution
Equation (VI) gives the expression for the distance between the nodes.
The above equation is independent of the amplitude term. Thus, even if the amplitude of the oscillator is doubled, the distance between the nodes do not change.
Conclusion:
Therefore, the distance between the nodes remains the same even if the amplitude of the oscillator is doubled.
Want to see more full solutions like this?
Chapter 18 Solutions
Physics for Scientists and Engineers: Foundations and Connections
- The 10-lb weight is supported by the cord AC and roller and by the spring that has a stiffness of k = 10 lb/in. and an unstretched length of 12 in. as shown in. Part A Determine the distance d to maintain equilibrium. Express your answer in inches to three significant figures. 節 ΕΠΙ ΑΣΦ d = *k J vec 5 t 0 ? d C A in. 12 in. Barrow_forwardThe members of a truss are connected to the gusset plate as shown in . The forces are concurrent at point O. Take = 90° and T₁ = 7.5 kN. Part A Determine the magnitude of F for equilibrium. Express your answer to three significant figures and include the appropriate units. F = Value Submit Request Answer Part B 0 ? Units Determine the magnitude of T2 for equilibrium. Express your answer to three significant figures and include the appropriate units. ? T₂ = Value Units T₁ Carrow_forwardpls help on botharrow_forward
- pls helparrow_forwardpls helparrow_forward6. 6. There are 1000 turns on the primary side of a transformer and 200 turns on thesecondary side. If 440 V are supplied to the primary winding, what is the voltageinduced in the secondary winding? Is this a step-up or step-down transformer? 7. 80 V are supplied to the primary winding of a transformer that has 50 turns. If thesecondary side has 50,000 turns, what is the voltage induced on the secondary side?Is this a step-up or step-down transformer? 8. There are 50 turns on the primary side of a transformer and 500 turns on thesecondary side. The current through the primary winding is 6 A. What is the turnsratio of this transformer? What is the current, in milliamps, through the secondarywinding?9. The current through the primary winding on a transformer is 5 A. There are 1000turns on the primary winding and 20 turns on the secondary winding. What is theturns ratio of this transformer? What is the current, in amps, through the secondarywinding?arrow_forward
- No chatgpt plsarrow_forwardWhat is the current, in amps, across a conductor that has a resistance of10 Ω and a voltage of 20 V? 2. A conductor draws a current of 100 A and a resistance of 5 Ω. What is thevoltageacross the conductor? 3. What is the resistance, in ohm’s, of a conductor that has a voltage of 80 kVand acurrent of 200 mA? 4. An x-ray imaging system that draws a current of 90 A is supplied with 220V. What is the power consumed? 5. An x-ray is produced using 800 mA and 100 kV. What is the powerconsumed in kilowatts?arrow_forwardՍՈՈՒ XVirginia Western Community Coll x P Course Home X + astering.pearson.com/?courseld=13289599#/ Figure y (mm) x=0x = 0.0900 m All ✓ Correct For either the time for one full cycle is 0.040 s; this is the period. Part C - ON You are told that the two points x = 0 and x = 0.0900 m are within one wavelength of each other. If the wave is moving in the +x-direction, determine the wavelength. Express your answer to two significant figures and include the appropriate units. 0 t(s) λ = Value m 0.01 0.03 0.05 0.07 Copyright © 2025 Pearson Education Inc. All rights reserved. 日 F3 F4 F5 1775 % F6 F7 B F8 Submit Previous Answers Request Answer ? × Incorrect; Try Again; 3 attempts remaining | Terms of Use | Privacy Policy | Permissions | Contact Us | Cookie Settings 28°F Clear 4 9:23 PM 1/20/2025 F9 prt sc F10 home F11 end F12 insert delete 6 7 29 & * ( 8 9 0 t = back Οarrow_forward
- Part C Find the height yi from which the rock was launched. Express your answer in meters to three significant figures. Learning Goal: To practice Problem-Solving Strategy 4.1 for projectile motion problems. A rock thrown with speed 12.0 m/s and launch angle 30.0 ∘ (above the horizontal) travels a horizontal distance of d = 19.0 m before hitting the ground. From what height was the rock thrown? Use the value g = 9.800 m/s2 for the free-fall acceleration. PROBLEM-SOLVING STRATEGY 4.1 Projectile motion problems MODEL: Is it reasonable to ignore air resistance? If so, use the projectile motion model. VISUALIZE: Establish a coordinate system with the x-axis horizontal and the y-axis vertical. Define symbols and identify what the problem is trying to find. For a launch at angle θ, the initial velocity components are vix=v0cosθ and viy=v0sinθ. SOLVE: The acceleration is known: ax=0 and ay=−g. Thus, the problem becomes one of…arrow_forwardPhys 25arrow_forwardPhys 22arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





