
Concept explainers
As in Figure P18.16, a simple harmonic oscillator is attached to a rope of linear mass density 5.4 × 10−2 kg/m, creating a standing transverse wave. There is a 3.6-kg block hanging from the other end of the rope over a pulley. The oscillator has an angular frequency of 43.2 rad/s and an amplitude of 24.6 cm. a. What is the distance between adjacent nodes? b. If the angular frequency of the oscillator doubles, what happens to the distance between adjacent nodes? c. If the mass of the block is doubled instead, what happens to the distance between adjacent nodes? d. If the amplitude of the oscillator is doubled, what happens to the distance between adjacent nodes?
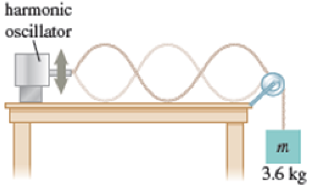
FIGURE P18.16
(a)
The distance between the adjacent nodes.
Answer to Problem 16PQ
The distance between the adjacent nodes is
Explanation of Solution
Given that the linear mass density of the rope is
Write the expression for the wavelength of the wave.
Here,
Write the expression for the speed of the wave.
Here,
Write the equation to find the frequency of the wave.
Here,
Use equation (III) and (II) in (I).
Write the expression for the tension force on the rope (it is equal to the weight of the block hanged).
Here,
Use above expression in equation (IV).
The distance between the adjacent nodes is equal to half the wavelength of the wave.
Rewrite above equation using equation (V).
Conclusion:
Substitute
Therefore, the distance between the adjacent nodes is
(b)
The distance between the adjacent nodes when the angular frequency is doubled.
Answer to Problem 16PQ
The distance between the adjacent nodes when the angular frequency is doubled is
Explanation of Solution
Equation (VI) gives the expression for the distance between the nodes.
From the above equation it is clear that wavelength is inversely proportional to angular frequency.
The angular frequency is doubled. Replace
Conclusion:
Substitute
Therefore, distance between the adjacent nodes when the angular frequency is doubled is
(c)
The distance between the adjacent nodes if the mass of the block is doubled.
Answer to Problem 16PQ
The distance between the adjacent nodes if the mass of the block is doubled is
Explanation of Solution
Equation (VI) gives the expression for the distance between the nodes.
When the mass of the block is doubled,
Conclusion:
Substitute
Therefore, the distance between the adjacent nodes if the mass of the block is doubled is
(d)
The distance between the nodes if the amplitude of the oscillator is doubled.
Answer to Problem 16PQ
The distance between the nodes remains the same even if the amplitude of the oscillator is doubled.
Explanation of Solution
Equation (VI) gives the expression for the distance between the nodes.
The above equation is independent of the amplitude term. Thus, even if the amplitude of the oscillator is doubled, the distance between the nodes do not change.
Conclusion:
Therefore, the distance between the nodes remains the same even if the amplitude of the oscillator is doubled.
Want to see more full solutions like this?
Chapter 18 Solutions
Physics For Scientists And Engineers: Foundations And Connections, Extended Version With Modern Physics
- A car is traveling at top speed on the Bonneville salt flats while attempting a land speed record. The tires exert 25 kN of force in the backward direction on the ground. Why backwards? How large are the forces resisting the forward motion of the car, and why?arrow_forwardA bee strikes a windshield of a car on the freeway and gets crushed. What can you conclude about the force on the bee versus the force on the windshield, and on what principle is this based?arrow_forwardNo chatgpt plsarrow_forward
- No chatgpt plsarrow_forwardPlease help by: Use a free body diagram Show the equations State your assumptions Show your steps Box your final answer Thanks!arrow_forwardPlease help by: Use a free body diagram Show the equations State your assumptions Show your steps Box your final answer Thanks!arrow_forward
- By please don't use Chatgpt will upvote and give handwritten solutionarrow_forwardA collection of electric charges that share a common magnitude q (lower case) has been placed at the corners of a square, and an additional charge with magnitude Q (upper case) is located at the center of that square. The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four unique setups of charges are displayed. By moving one of the direction drawings from near the bottom to the bucket beside each of the setups, indicate the direction of the net electric force on the charge with magnitude Q, located near the center, else indicate that the magnitude of the net electric force is zero, if appropriate.arrow_forwardA number of electric charges has been placed at distinct points along a line with separations as indicated. Two charges share a common magnitude, q (lower case), and another charge has magnitude Q(upper case). The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four different configurations of charges are shown. For each, express the net electric force on the charge with magnitude Q (upper case) as F⃗E=FE,xî where the positive x direction is towards the right. By repositioning the figures to the area on the right, rank the configurations from the most negative value to the most positive value of FE,x.arrow_forward
- For each part make sure to include sign to represent direction, with up being positive and down being negative. A ball is thrown vertically upward with a speed of 30.5 m/s. A) How high does it rise? y= B) How long does it take to reach its highest point? t= C) How long does it take the ball return to its starting point after it reaches its highest point? t= D) What is its velocity when it returns to the level from which it started? v=arrow_forwardFour point charges of equal magnitude Q = 55 nC are placed on the corners of a rectangle of sides D1 = 27 cm and D2 = 11cm. The charges on the left side of the rectangle are positive while the charges on the right side of the rectangle are negative. Use a coordinate system where the positive y-direction is up and the positive x-direction is to the right. A. Which of the following represents a free-body diagram for the charge on the lower left hand corner of the rectangle? B. Calculate the horizontal component of the net force, in newtons, on the charge which lies at the lower left corner of the rectangle.Numeric : A numeric value is expected and not an expression.Fx = __________________________________________NC. Calculate the vertical component of the net force, in newtons, on the charge which lies at the lower left corner of the rectangle.Numeric : A numeric value is expected and not an expression.Fy = __________________________________________ND. Calculate the magnitude of the…arrow_forwardPoint charges q1=50.0μC and q2=-35μC are placed d1=1.0m apart, as shown. A. A third charge, q3=25μC, is positioned somewhere along the line that passes through the first two charges, and the net force on q3 is zero. Which statement best describes the position of this third charge?1) Charge q3 is to the right of charge q2. 2) Charge q3 is between charges q1 and q2. 3) Charge q3 is to the left of charge q1. B. What is the distance, in meters, between charges q1 and q3? (Your response to the previous step may be used to simplify your solution.)Give numeric value.d2 = __________________________________________mC. Select option that correctly describes the change in the net force on charge q3 if the magnitude of its charge is increased.1) The magnitude of the net force on charge q3 would still be zero. 2) The effect depends upon the numeric value of charge q3. 3) The net force on charge q3 would be towards q2. 4) The net force on charge q3 would be towards q1. D. Select option that…arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





