Calculus: Early Transcendentals (3rd Edition)
3rd Edition
ISBN: 9780134763644
Author: William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 17.1, Problem 52E
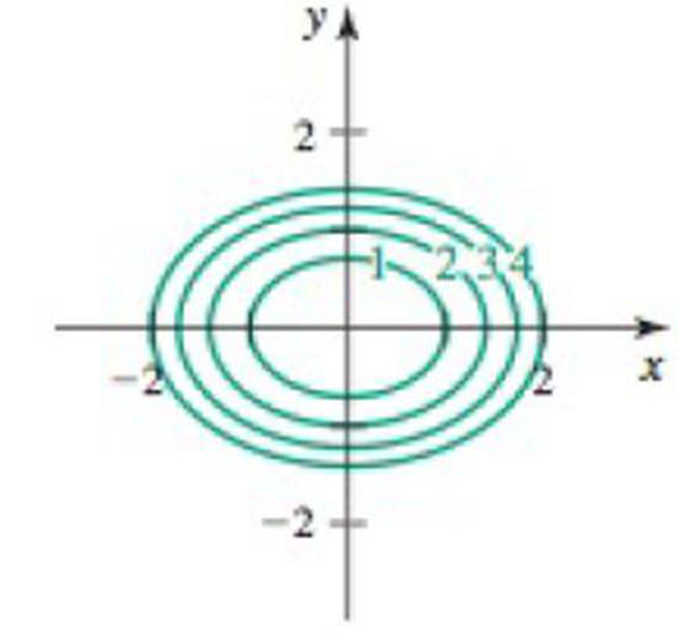
Equipotential curves Consider the following potential functions and graphs of their equipotential curves.
a. Find the associated gradient field F = ▿ϕ.
b. Show that the
c. Show that the vector field is orthogonal to the equipotential curve at all points (x, y).
d. Sketch two flow curves representing F that are everywhere orthogonal to the equipotential curves.
40. ϕ (x, y) = x2+ 2y2
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Determine if each of the following vector fields is the gradient of a function f(x, y). If so, find all of the
functions with this gradient.
(a) (3x² + e¹0) i + (10x e¹0 - 9 siny) j
(b) (10x el0y 9 sin y) i + (3x² + e¹0y) j
a) I have placed my work and my answer on my answer sheet
Gradient fields on curves For the potential function φ and points A, B, C, and D on the level curve φ(x, y) = 0, complete the following steps.a. Find the gradient field F = ∇φ.b. Evaluate F at the points A, B, C, and D.c. Plot the level curve φ(x, y) = 0 and the vectors F at the points A, B, C, and D.
φ(x, y) = y - 2x; A(-1, -2), B(0, 0), C(1, 2), and D(2, 4)
Plz solve part c
Chapter 17 Solutions
Calculus: Early Transcendentals (3rd Edition)
Ch. 17.1 - If the vector field in Example 1c describes the...Ch. 17.1 - In Example 2, verify that g(x, y). G(x, y) = 0. In...Ch. 17.1 - Find the gradient field associated with the...Ch. 17.1 - How is a vector field F = f, g, h used to describe...Ch. 17.1 - Sketch the vector field F = x, y.Ch. 17.1 - Prob. 3ECh. 17.1 - Given a differentiable, scalar-valued function ,...Ch. 17.1 - Interpret the gradient field of the temperature...Ch. 17.1 - Show that all the vectors in vector field...Ch. 17.1 - Sketch a few representative vectors of vector...
Ch. 17.1 - Sketching vector fields Sketch the following...Ch. 17.1 - Sketching vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Prob. 20ECh. 17.1 - Three-dimensional vector fields Sketch a few...Ch. 17.1 - Three-dimensional vector fields Sketch a few...Ch. 17.1 - Three-dimensional vector fields Sketch a few...Ch. 17.1 - Matching vector Fields with graphs Match vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Explain why or why not Determine whether the...Ch. 17.1 - Electric field due to a point charge The electric...Ch. 17.1 - Electric field due to a line of charge The...Ch. 17.1 - Gravitational force due to a mass The...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Prob. 62ECh. 17.1 - Prob. 63ECh. 17.1 - Prob. 64ECh. 17.1 - Prob. 65ECh. 17.1 - Vector fields in polar coordinates A vector field...Ch. 17.1 - Cartesian-to-polar vector field Write the vector...Ch. 17.2 - Explain mathematically why differentiating the arc...Ch. 17.2 - Suppose r(t) = t,0, for a t b, is a parametric...Ch. 17.2 - Prob. 3QCCh. 17.2 - Suppose a two dimensional force field is...Ch. 17.2 - Prob. 5QCCh. 17.2 - How does a line integral differ from the...Ch. 17.2 - If a curve C is given by r(t) = t, t2, what is...Ch. 17.2 - Prob. 3ECh. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find an expression for the vector field F = x y,...Ch. 17.2 - Suppose C is the curve r(t) = t,t3, for 0 t 2,...Ch. 17.2 - Suppose C is the circle r(l) = cos l, sin l , for...Ch. 17.2 - State two other forms for the line integral CFTds...Ch. 17.2 - Assume F is continuous on a region containing the...Ch. 17.2 - Assume F is continuous on a region containing the...Ch. 17.2 - How is the circulation of a vector field on a...Ch. 17.2 - Prob. 16ECh. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals in 3Convert the line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals in 3Convert the line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Mass and density A thin wire represented by the...Ch. 17.2 - Mass and density A thin wire represented by the...Ch. 17.2 - Average values Find the average value of the...Ch. 17.2 - Average values Find the average value of the...Ch. 17.2 - Length of curves Use a scalar line integral to...Ch. 17.2 - Length of curves Use a scalar line integral to...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - 47–48. Line integrals from graphs Determine...Ch. 17.2 - Line integrals from graphs Determine whether c F ...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Circulation Consider the following vector fields F...Ch. 17.2 - Circulation Consider the following vector fields F...Ch. 17.2 - Flux Consider the vector fields and curves in...Ch. 17.2 - Flux Consider the vector fields and curves in...Ch. 17.2 - Explain why or why not Determine whether the...Ch. 17.2 - Flying into a headwind An airplane flies in the...Ch. 17.2 - Flying into a headwind
How does the result of...Ch. 17.2 - Prob. 64ECh. 17.2 - Changing orientation Let f(x, y) = x and let C be...Ch. 17.2 - Work in a rotation field Consider the rotation...Ch. 17.2 - Work in a hyperbolic field Consider the hyperbolic...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Flux across curves in a vector field Consider the...Ch. 17.2 - Prob. 74ECh. 17.2 - Zero circulation fields 57.Consider the vector...Ch. 17.2 - Zero flux fields 58.For what values of a and d...Ch. 17.2 - Zero flux fields 59.Consider the vector field F =...Ch. 17.2 - Heat flux in a plate A square plate R = {(x, y): 0...Ch. 17.2 - Prob. 79ECh. 17.2 - Line integrals with respect to dx and dy Given a...Ch. 17.2 - Looking ahead: Area from line integrals The area...Ch. 17.2 - Prob. 82ECh. 17.3 - Is a figure-8 curve simple? Closed? Is a torus...Ch. 17.3 - Explain why a potential function for a...Ch. 17.3 - Verify by differentiation that the potential...Ch. 17.3 - Explain why the vector field (xy + xz yz) is...Ch. 17.3 - What does it mean for a function to have an...Ch. 17.3 - What are local maximum and minimum values of a...Ch. 17.3 - What conditions must be met to ensure that a...Ch. 17.3 - How do you determine whether a vector field in 3...Ch. 17.3 - Briefly describe how to find a potential function ...Ch. 17.3 - If F is a conservative vector field on a region R,...Ch. 17.3 - If F is a conservative vector field on a region R,...Ch. 17.3 - Give three equivalent properties of conservative...Ch. 17.3 - How do you determine the absolute maximum and...Ch. 17.3 - Explain how a function can have an absolute...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Designing a function Sketch a graph of a function...Ch. 17.3 - Finding Potential functions Determine Whether the...Ch. 17.3 - Designing a function Sketch a graph of a function...Ch. 17.3 - Designing a function Sketch a graph of a function...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integral...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Evaluating line integral using level curves...Ch. 17.3 - Evaluating line integral using level curves...Ch. 17.3 - Line integrals Evaluate each line integral using a...Ch. 17.3 - Line integrals Evaluate each line integral using a...Ch. 17.3 - Line integrals Evaluate the following line...Ch. 17.3 - Line integrals Evaluate the following line...Ch. 17.3 - Prob. 57ECh. 17.3 - Prob. 58ECh. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Suppose C is a circle centered at the origin in a...Ch. 17.3 - A vector field that is continuous in R2 is given...Ch. 17.3 - Prob. 65ECh. 17.3 - Conservation of energy Suppose an object with mass...Ch. 17.3 - Gravitational potential The gravitational force...Ch. 17.3 - Radial Fields in 3 are conservative Prove that the...Ch. 17.3 - 55.Rotation fields are usually not conservative...Ch. 17.3 - Linear and quadratic vector fields a.For what...Ch. 17.3 - Prob. 71ECh. 17.3 - Prob. 72ECh. 17.3 - Prob. 73ECh. 17.3 - Prob. 74ECh. 17.3 - Prob. 75ECh. 17.4 - Compute gxfy for the radial vector field...Ch. 17.4 - Compute fxgy for the radial vector field...Ch. 17.4 - Prob. 3QCCh. 17.4 - Explain why Greens Theorem proves that if gx = fy,...Ch. 17.4 - Explain why the two forms of Greens Theorem are...Ch. 17.4 - Referring to both forms of Greens Theorem, match...Ch. 17.4 - Prob. 3ECh. 17.4 - Why does a two-dimensional vector field with zero...Ch. 17.4 - Why does a two-dimensional vector field with zero...Ch. 17.4 - Sketch a two-dimensional vector field that has...Ch. 17.4 - Sketch a two-dimensional vector field that has...Ch. 17.4 - Discuss one of the parallels between a...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Prob. 12ECh. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Suppose C is the boundary of region R = {(x, y):x2...Ch. 17.4 - Suppose C is the boundary of region R = {(x, y):...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Greens Theorem, flux form Consider the following...Ch. 17.4 - Greens Theorem, flux form Consider the following...Ch. 17.4 - Greens Theorem, flux form Consider the following...Ch. 17.4 - Greens theorem, flux form Consider the following...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - 3140. Line integrals Use Greens Theorem to...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - Circulation and flux For the following vector...Ch. 17.4 - Circulation and flux for the following vector...Ch. 17.4 - Circulation and flux For the following vector...Ch. 17.4 - Circulation and flux For the following vector...Ch. 17.4 - Explain why or why not Determine whether the...Ch. 17.4 - Special line integrals Prove the following...Ch. 17.4 - Special line integrals Prove the following...Ch. 17.4 - Prob. 52ECh. 17.4 - Area line integral Show that the value of...Ch. 17.4 - Area line integral In terms of the parameters a...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Prob. 63ECh. 17.4 - Greens Theorem as a Fundamental Theorem of...Ch. 17.4 - Greens Theorem as a Fundamental Theorem of...Ch. 17.4 - Whats wrong? Consider the rotation field...Ch. 17.4 - Whats wrong? Consider the radial field...Ch. 17.4 - Prob. 68ECh. 17.4 - Flux integrals Assume the vector field F = (f, g)...Ch. 17.4 - Streamlines are tangent to the vector field Assume...Ch. 17.4 - Streamlines and equipotential lines Assume that on...Ch. 17.4 - Channel flow The flow in a long shallow channel is...Ch. 17.5 - Show that is a vector field has the form...Ch. 17.5 - Verify the claim made in Example 3d by showing...Ch. 17.5 - Show that is a vector field has the form...Ch. 17.5 - Is (uF) a vector function or a scalar function?Ch. 17.5 - Explain how to compute the divergence of the...Ch. 17.5 - Interpret the divergence of a vector field.Ch. 17.5 - What does it mean if the divergence of a vector...Ch. 17.5 - Explain how to compute the curl of the vector...Ch. 17.5 - Interpret the curl of a general rotation vector...Ch. 17.5 - What does it mean if the curl of a vector field is...Ch. 17.5 - What is the value of ( F)?Ch. 17.5 - What is the value of u?Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence and flux from graphs Consider the...Ch. 17.5 - Divergence and flux from graphs Consider the...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Explain why or why not Determine whether the...Ch. 17.5 - Another derivative combination Let F = (f, g, h)...Ch. 17.5 - Does it make sense? Are the following expressions...Ch. 17.5 - Zero divergence of the rotation field Show that...Ch. 17.5 - General rotation fields a.Let a = (0, 1, 0), r =...Ch. 17.5 - Prob. 44ECh. 17.5 - Curl of the rotation field For the general...Ch. 17.5 - Inward to outward Find the exact points on the...Ch. 17.5 - Maximum divergence Within the cube {(x, y, z): |x|...Ch. 17.5 - Maximum curl Let F =
Find the scalar component of...Ch. 17.5 - Zero component of the curl For what vectors n is...Ch. 17.5 - Prob. 50ECh. 17.5 - Find a vector Field Find a vector field F with the...Ch. 17.5 - Prob. 52ECh. 17.5 - Paddle wheel in a vector field Let F = z, 0, 0 and...Ch. 17.5 - Angular speed Consider the rotational velocity...Ch. 17.5 - Angular speed Consider the rotational velocity...Ch. 17.5 - Heat flux Suppose a solid object in 3 has a...Ch. 17.5 - Heat flux Suppose a solid object in 3 has a...Ch. 17.5 - Prob. 58ECh. 17.5 - Gravitational potential The potential function for...Ch. 17.5 - Electric potential The potential function for the...Ch. 17.5 - Navier-Stokes equation The Navier-Stokes equation...Ch. 17.5 - Stream function and vorticity The rotation of a...Ch. 17.5 - Amperes Law One of Maxwells equations for...Ch. 17.5 - Prob. 64ECh. 17.5 - Properties of div and curl Prove the following...Ch. 17.5 - Prob. 66ECh. 17.5 - Identities Prove the following identities. Assume...Ch. 17.5 - Identities Prove the following identities. Assume...Ch. 17.5 - Prob. 69ECh. 17.5 - Prob. 70ECh. 17.5 - Prob. 71ECh. 17.5 - Prob. 72ECh. 17.5 - Prob. 73ECh. 17.5 - Gradients and radial fields Prove that for a real...Ch. 17.5 - Prob. 75ECh. 17.6 - Describe the surface r(u, v) = 2cosu,2sinu,v,for 0...Ch. 17.6 - Describe the surface r(u, v) = vcosu,vsinu,v, for...Ch. 17.6 - Describe the surface r(u, v) =...Ch. 17.6 - Prob. 4QCCh. 17.6 - Explain why explicit description for a cylinder x2...Ch. 17.6 - Explain why the upward flux for the radial field...Ch. 17.6 - Give a parametric description for a cylinder with...Ch. 17.6 - Prob. 2ECh. 17.6 - Give a parametric description for a sphere with...Ch. 17.6 - Prob. 4ECh. 17.6 - Explain how to compute the surface integral of a...Ch. 17.6 - Explain what it means for a surface to be...Ch. 17.6 - Describe the usual orientation of a closed surface...Ch. 17.6 - Why is the upward flux of a vertical vector field...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Average Values 39. Find the average temperature on...Ch. 17.6 - Average values 40.Find the average squared...Ch. 17.6 - Average values 41.Find the average value of the...Ch. 17.6 - Average values 42.Find the average value of the...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Explain why or why not Determine whether the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Cone and sphere The cone z2 = x2 + y2 for z 0,...Ch. 17.6 - Cylinder and sphere Consider the sphere x2 + y2 +...Ch. 17.6 - Flux on a tetrahedron Find the upward flux of the...Ch. 17.6 - Flux across a cone Consider the field F = x, y, z...Ch. 17.6 - Surface area formula for cones Find the general...Ch. 17.6 - Surface area formula for spherical cap A sphere of...Ch. 17.6 - Radial fields and spheres Consider the radial...Ch. 17.6 - Heat flux The heat flow vector field for...Ch. 17.6 - Heat flux The heat flow vector field for...Ch. 17.6 - Prob. 63ECh. 17.6 - Flux across a cylinder Let S be the cylinder x2 +...Ch. 17.6 - Flux across concentric spheres Consider the radial...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Outward normal to a sphere Show that...Ch. 17.6 - Special case of surface integrals of scalar-valued...Ch. 17.6 - Surfaces of revolution Suppose y = f(x) is a...Ch. 17.6 - Rain on roofs Let z = s(x, y) define a surface...Ch. 17.6 - Surface area of a torus a.Show that a torus with...Ch. 17.6 - Surfaces of revolution single variable Let f be...Ch. 17.7 - Suppose S is a region in the xy-plane with a...Ch. 17.7 - In Example 3a We used the parameterization r(t) =...Ch. 17.7 - In Example 4, explain why a paddle wheel with its...Ch. 17.7 - Explain the meaning of the integral S(F)ndS in...Ch. 17.7 - Explain the meaning of the integral S(F)ndS in...Ch. 17.7 - Explain the meaning of Stokes Theorem.Ch. 17.7 - Why does a conservative vector field produce zero...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Explain why or why not Determine whether the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Prob. 38ECh. 17.7 - Circulation in a plane A circle C in the plane x +...Ch. 17.7 - No integrals Let F = (2z, z, 2y + x) and let S be...Ch. 17.7 - Compound surface and boundary Begin with the...Ch. 17.7 - Ampres Law The French physicist AndrMarie Ampre...Ch. 17.7 - Maximum surface integral Let S be the paraboloid z...Ch. 17.7 - Area of a region in a plane Let R be a region in a...Ch. 17.7 - Choosing a more convenient surface The goal is to...Ch. 17.7 - Radial fields and zero circulation Consider the...Ch. 17.7 - Zero curl Consider the vector field...Ch. 17.7 - Average circulation Let S be a small circular disk...Ch. 17.7 - Proof of Stokes Theorem Confirm the following step...Ch. 17.7 - Stokes Theorem on closed surfaces Prove that if F...Ch. 17.7 - Rotated Greens Theorem Use Stokes Theorem to write...Ch. 17.8 - Interpret the Divergence Theorem in the case that...Ch. 17.8 - In Example 3. does the vector field have negative...Ch. 17.8 - Draw unit cube D = {(x, y, z) : 0 x 1, 0 y 1, 0...Ch. 17.8 - Review Questions 1.Explain the meaning of the...Ch. 17.8 - Interpret the volume integral in the Divergence...Ch. 17.8 - Explain the meaning of the Divergence Theorem.Ch. 17.8 - What is the net outward flux of the rotation field...Ch. 17.8 - What is the net outward flux of the radial field F...Ch. 17.8 - What is the divergence of an inverse square vector...Ch. 17.8 - Suppose div F = 0 in a region enclosed by two...Ch. 17.8 - If div F 0 in a region enclosed by a small cube,...Ch. 17.8 - Verifying the Divergence Theorem Evaluate both...Ch. 17.8 - F = x, y, z; D = {(x, y, z): |x| 1, |y| 1, |z| ...Ch. 17.8 - Basic Skills 912.Verifying the Divergence Theorem...Ch. 17.8 - F = x2, y2, z2; D = {(x, y, z): |x| 1, |y| 2,...Ch. 17.8 - Rotation fields 13.Find the net outward flux of...Ch. 17.8 - Rotation fields 14.Find the net outward flux of...Ch. 17.8 - Find the net outward flux of the field F = bz cy,...Ch. 17.8 - Rotation fields 16.Find the net outward flux of F...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - F = x, 2y, z; S is the boundary of the tetrahedron...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - F = y 2x, x3 y, y2 z; S is the sphere {(x, y,...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - F = x2, y2, z2); D is the region in the first...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Explain why or why not Determine whether the...Ch. 17.8 - Flux across a sphere Consider the radial field F =...Ch. 17.8 - Flux integrals Compute the outward flux of the...Ch. 17.8 - Flux integrals Compute the outward flux of the...Ch. 17.8 - Flux integrals Compute the outward flux of the...Ch. 17.8 - Radial fields Consider the radial vector field...Ch. 17.8 - Singular radial field Consider the radial field...Ch. 17.8 - Logarithmic potential Consider the potential...Ch. 17.8 - Gauss Law for electric fields The electric field...Ch. 17.8 - Gauss Law for gravitation The gravitational force...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Inverse square fields are special Let F be a...Ch. 17.8 - A beautiful flux integral Consider the potential...Ch. 17.8 - Integration by parts (Gauss' Formula) Recall the...Ch. 17.8 - Prob. 49ECh. 17.8 - Prob. 50ECh. 17.8 - Greens Second Identity Prose Greens Second...Ch. 17.8 - Prob. 52ECh. 17.8 - Prob. 53ECh. 17.8 - Prob. 54ECh. 17 - Explain why or why not Determine whether the...Ch. 17 - Matching vector fields Match vector fields a-f...Ch. 17 - Gradient fields in 2 Find the vector field F = ...Ch. 17 - Gradient fields in 2 Find the vector field F = ...Ch. 17 - Gradient fields in 3 Find the vector field F = ...Ch. 17 - Gradient fields in 3 Find the vector field F = ...Ch. 17 - Normal component Let C be the circle of radius 2...Ch. 17 - Line integrals Evaluate the following line...Ch. 17 - Line integrals Evaluate the following line...Ch. 17 - Line integrals Evaluate the following line...Ch. 17 - Two parameterizations Verify that C(x2y+3z)ds has...Ch. 17 - Work integral Find the work done in moving an...Ch. 17 - Work integrals in R3 Given the following force...Ch. 17 - Work integrals in 3 Given the following force...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Flux in channel flow Consider the flow of water in...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Radial fields in R2 are conservative Prove that...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Areas of plane regions Find the area of the...Ch. 17 - Areas of plane regions Find the area of the...Ch. 17 - Circulation and flux Consider the following vector...Ch. 17 - Circulation and flux Consider the following vector...Ch. 17 - Parameters Let F = ax + by, cx + dy, where a, b,...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Identities Prove that (1|r|4)=4r|r|6 and use the...Ch. 17 - Maximum curl Let F=z,x,y. a. What is the scalar...Ch. 17 - Paddle wheel in a vector field Let F = 0, 2x, 0...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface integrals Evaluate the following surface...Ch. 17 - Surface integrals Evaluate the following surface...Ch. 17 - Surface integrals Evaluate the following surface...Ch. 17 - Flux integrals Find the flux of the following...Ch. 17 - Flux integrals Find the flux of the following...Ch. 17 - Three methods Find the surface area of the...Ch. 17 - Flux across hemispheres and paraboloids Let S be...Ch. 17 - Surface area of an ellipsoid Consider the...Ch. 17 - Stokes Theorem for line integrals Evaluate the...Ch. 17 - Stokes Theorem for line integrals Evaluate the...Ch. 17 - Stokes Theorem for surface integrals Use Stokes...Ch. 17 - Stokes Theorem for surface integrals Use Stokes...Ch. 17 - Conservative fields Use Stokes Theorem to find the...Ch. 17 - Computing fluxes Use the Divergence Theorem to...Ch. 17 - Computing fluxes Use the Divergence Theorem to...Ch. 17 - Computing fluxes Use the Divergence Theorem to...Ch. 17 - General regions Use the Divergence Theorem to...Ch. 17 - General regions Use the Divergence Theorem to...Ch. 17 - Flux integrals Compute the outward flux of the...Ch. 17 - Stokes Theorem on a compound surface Consider the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The intercepts of the equation 9 x 2 +4y=36 are ______. (pp.18-19)
Precalculus Enhanced with Graphing Utilities (7th Edition)
Evaluate each expression.
Glencoe Math Accelerated, Student Edition
Other techniques Evaluate the following limits, where a and b are fixed real numbers. 49. limxaxaxa,a0
Single Variable Calculus: Early Transcendentals (2nd Edition) - Standalone book
Fish Population with Harvesting The fish population in a pond with carrying capacity 1000 is modeled by the log...
Calculus & Its Applications (14th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- A net is dipped in a river. Determine the flow rate of water across the net if the velocity vector field for the river is given by = (x - y, z + y + 9, z) and the net is decribed by the equation y = V1-x - z, y 2 0, and oriented in the positive y- direction. (Use symbolic notation and fractions where needed.) V. dS =arrow_forwardMatch each of the following three vector fields to one of the four vector fields graphed below (yes, one graph does not have a match), and then explain your thinking: 1. (a) F(x, y) = (2y, 2.r). Match (circle one): I II III IV (b) F(x, y) = (x², 2y). Match (circle one): I II III IV (c) F(x, y) = (x², y²). Match (circle one): I II III IV (d) Explain your choices. Explanation:arrow_forwardDetermine if the vector fields below are conservative. Find potential functions where possible. (a.) F(x, y) = (2x — sin(x + y²), −2y sin(x + y²)) (b.) F(x, y) = (-y, x) (c.) F(y, z) = (z+y²y+z³)arrow_forward
- Need the sketch of it as wellarrow_forwardLet A be the vector potential and B the magnetic field of the infinite solenoid of radius R. Then { B(r) = A(r) = √x² + y2 is the distance to the z-axis and B is a constant that depends on the current strength I and the spacing of where r = the turns of wire. The vector potential for B is S 0 Incorrect Bk if Jc if r> R r R B(-y, x,0) ifarrow_forwardFourier's Law of heat transfer (or heat conduction) states that the heat flow vector F at a point is proportional to the negative gradient of the temperature: that is, F= -kVT, which means that heat energy flows from hot regions to cold regions. The constant k is called the conductivity, which has metric units of J/m-s-K or W/m-K. A temperature function T for a region D is given below. Find the net outward heat flux SSF•nds= - kff triple integral. Assume that k = 1. T(x,y,z)=110e-x²-y²-2². D is the sphere of radius a centered at the origin. The net outward heat flux across the boundary is. (Type an exact answer, using as needed.) G S VT.n dS across the boundary S of D. It may be easier to use the Divergence Theorem and evaluate aarrow_forwardThe figure shows a vector field F and three paths from P (-3,0) to Q= (3,0). The top and bottom paths T and B comprise a circle, and the middle path M is a line segment. Determine whether the following quantities are positive, negative, or zero, or answer true or false. Be sure you can explain your answers. (Click on graph to enlarge) (a) F dr is ? (b) F- dř is ? F. dr is ? (c) F-dr is 2 () (e) ? v True or False: F- dr () ? v True or False F is a gradient field.arrow_forwardA net is dipped in a river. Determine the flow rate of water across the net if the velocity vector field for the river is given by v = (x-y, z + y + 3, z²) and the net is decribed by the equation y = √1-x²-2², y ≥ 0, and oriented in the positive y- direction. (Use symbolic notation and fractions where needed.)arrow_forwardB8. Advance mathsarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.; Author: Math and Science;https://www.youtube.com/watch?v=BHRWArTFgTs;License: Standard YouTube License, CC-BY